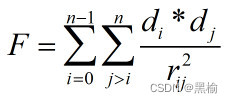| 实验目的及要求: 1、了解多项式插值公式的存在唯一性条件及其余项表达式的推导。 2、了解拉格朗日插值多项式的构造、计算及其基函数的特点,牛顿插值多项式的构造与应用,差商、差分的计算及基本性质。 实验内容: 1、编写Lagrange插值法、Newton插值法通用子程序,依据数据表
|
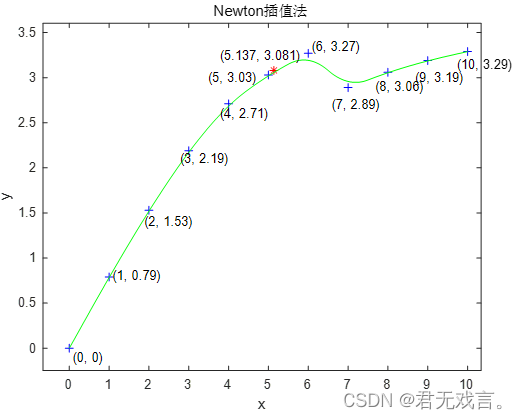
被调用的lagrange.m文件: function Y=lagrange(x,y,X) n=length(x); m=length(X); for i=1:m z=X(i);s=0; for k=1:n p=1; for j=1:n if j~=k p=p*(z-x(j))/(x(k)-x(j)); end end s=p*y(k)+s; end Y(i)=s; End 调用lagrange.m文件的cha_zhi.m执行文件: x=0:10; y=[0 0.79 1.53 2.19 2.71 3.03 3.27 2.89 3.06 3.19 3.29]; X=5.137; Y=lagrange(x,y,X) plot(x,y,'b+',X,Y,'r*') hold on %semilogy(x,y)%折线图 values = spcrv([[x(1) x x(end)];[y(1) y y(end)]],3); plot(values(1,:),values(2,:)) %光滑的曲线图图 %关于spcrv用法 %values = spcrv([[t(1) t t(end)];[y(1) y y(end)]],3); %plot(values(1,:),values(2,:));%直接plot只能生成折线图 %标点 text(0.1,-0.1,'(0, 0)') text(1.1,0.8,'(1, 0.79)') text(1.9,1.4,'(2, 1.53)') text(2.8,2.1,'(3, 2.19)') text(3.8,2.6,'(4, 2.71)') text(3.5,3.0,'(5, 3.03)') text(3.8,3.25,'(5.137, 3.081)') text(6.1,3.35,'(6, 3.27)') text(6.6,2.7,'(7, 2.89)') text(7.7,2.9,'(8, 3.06)') text(8.7,3,'(9, 3.19)') text(9.75,3.15,'(10, 3.29)') %关于text用法 %text( , ,'')前部分填写坐标,后部分''内为显示内容 Newton插值 算法分析
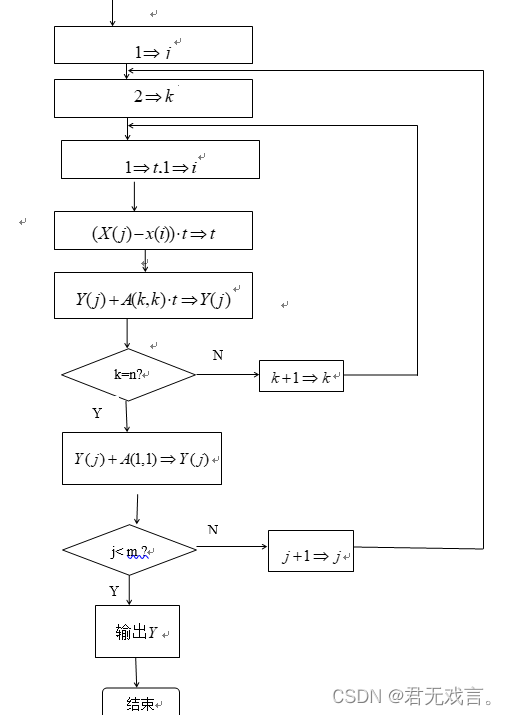
算法流程图
牛顿插值的MATLAB主程序 被调用的Newton.m文件: function Y=Newton(x,y,X) x=x(:); y=y(:); n=length(x); m=length(X); A=zeros(n,n); Y=0*X; A(:,1)=y; for j=2:n for i=j:n A(i,j)=(A(i,j-1)-A(i-1,j-1))/(x(i)-x(i-j+1)) %A(1,1)=f(x1),A(2,2)=f(x1,x2), …,A(n,n)=f(x1,x2, …xn) end end %用n-1次Newton插值多项式计算X中每个元素的近似值 for j=1:m for k=2:n t=1; for i=1:k-1 t=(X(j)-x(i))*t; end Y(j)=Y(j)+A(k,k)*t; end Y(j)=Y(j)+A(1,1); end 调用Newton.m文件的cha_zhi2.m执行文件: x=0:10; y=[0 0.79 1.53 2.19 2.71 3.03 3.27 2.89 3.06 3.19 3.29]; X=5.137; Y=Newton(x,y,X) plot(x,y,'b+',X,Y,'r*') hold on %semilogy(x,y)%折线图 values = spcrv([[x(1) x x(end)];[y(1) y y(end)]],3); plot(values(1,:),values(2,:)) %光滑的曲线图图 %关于spcrv用法 %values = spcrv([[t(1) t t(end)];[y(1) y y(end)]],3); %plot(values(1,:),values(2,:));%直接plot只能生成折线图 %标点 text(0.1,-0.1,'(0, 0)') text(1.1,0.8,'(1, 0.79)') text(1.9,1.4,'(2, 1.53)') text(2.8,2.1,'(3, 2.19)') text(3.8,2.6,'(4, 2.71)') text(3.5,3.0,'(5, 3.03)') text(3.8,3.25,'(5.137, 3.081)') text(6.1,3.35,'(6, 3.27)') text(6.6,2.7,'(7, 2.89)') text(7.7,2.9,'(8, 3.06)') text(8.7,3,'(9, 3.19)') text(9.75,3.15,'(10, 3.29)') %关于text用法 %text( , ,'')前部分填写坐标,后部分''内为显示内容
由以上实验已经求得近似值Y=3.080849054732755,设再取x4,x6为节点,用线性插值可以求得另外一个插值Y1,再由书第21页公式(15)可以得到误差值。 x=0:10; y=[0 0.79 1.53 2.19 2.71 3.03 3.27 2.89 3.06 3.19 3.29]; X=5.137; Y=lagrange(x,y,X) %Y1=y4+((y6-y4)/(x6-x4))/(5.137-x4) Y1=2.71+((3.27-2.71)/(6-4))*(5.137-4) %Z=((X-x5)/(x6-x5))*(Y1-Y) Z=((X-5)/(6-5))*(Y1-Y) 得到如下结果:
所以误差为:-0.007191000498387 可以得到新的近似值:Y2=Y+Z=3.073658054234368 运行结果: 1.拉格朗日插值法的运行结果:
2.牛顿插值法的运行结果
|
| 结果分析与讨论:
|
数学建模算法(基于matlab和python)之 Lagrange插值、Newton插值(1/10)
news2026/2/13 21:16:20
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/692511.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
ESP32设备驱动-74HC595驱动7段数码管
74HC595驱动7段数码管 文章目录 74HC595驱动7段数码管1、74HC595介绍2、硬件准备3、软件准备4、驱动实现所有微控制器都有特定数量的 IO 引脚,但在某些应用中,例如在 7 段显示器中,我们需要的 GPIO 引脚数量超过我们的控制器所能提供的数量。 对于这种需要多个输出引脚但微控…
深入分析动态链接的延迟绑定
关于程序运行的系列文章
ELF文件结构和实战分析 深入分析动态链接的延迟绑定 文章目录 为什么使用动态链接库?静态链接的问题:动态链接库 动态共享库是怎样存在于内存中的?动态链接 原理简析代码示例dynsymGOT.rela.dyn 和 .rela.pltPLT使用…
【云原生】一文学会Dockerfile所有常用命令
Docker file的作用方便管理员来根据需求来进行构建镜像,前面学习过commit来将一个容器打包成镜像,但是Docker 并不建议用户通过commit方式构建镜像。
原因如下:
1. 这是一种手工创建镜像的方式,容易出错,效率低且可重…
锁相环PLL原理及matlab代码
补偿相干系统中的激光器相位噪声。 根据Wiener process的性质,离得越近的符号相位噪声在概率统计上越相似,因此,可以用上一个符号估计得到的相位当做当前这个符号的初始相位,再通过判决来估计当前符号的准确相位,这就是…
寻找失落的数字:让有序数组完美覆盖的最小区间范围
本篇博客会讲解力扣“228. 汇总区间”的解题思路,这是题目链接。 解题思路:使用left和right来维护有序区间的左右端点。一开始,left和right都初始化为0。注意,不能把right初始化成1,因为当数组只有1个元素时࿰…
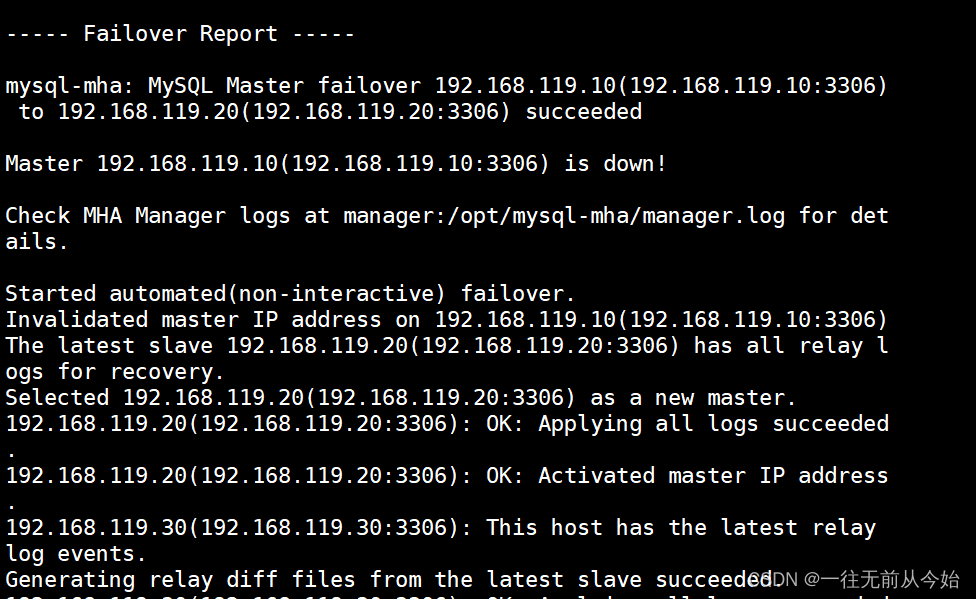
MySQL 高可用配置及故障切换
MySQL 高可用配置及故障切换 一、MHA1.1 什么是 MHA1.2 MHA 的组成1.3 MHA 的特点1.4 MHA工作原理 二、搭建 MySQL MHA2.1 实验思路2.2 部署过程2.3 环境准备2.4 搭建MHA 一、MHA
1.1 什么是 MHA
1、MHA(MasterHigh Availability)是一套优秀的MySQL高可…
华为举办5G商业对话沙龙,携手运营商共促5G产业再升级
【中国,上海,2023年06月27日】在2023 MWC 上海期间,华为举办“5G商业对话沙龙”,旨在面向国内外运营商,搭建产业深度交流和求策问计的对话平台,共同促进5G产业再升级。会议期间,与会嘉宾达成一致…
回收站数据恢复方法 回收站清空如何恢复数据
在日常使用计算机时,我们经常会不小心删除文件或者清空回收站,导致重要的数据似乎丢失。然而,在某些情况下,我们仍然有可能通过一些回收站数据恢复方法来找回已经被清空的回收站中的数据。今天我们一起来了解一下回收站数据恢复方…
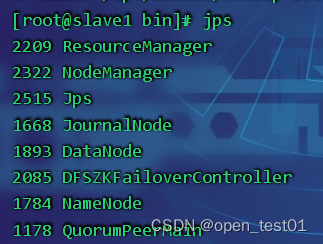
HadoopHA搭建
主机设置
三台主机关闭防火墙
三台主机关闭SeLinux安全机制
给每台主机修改主机名
配置三台主机地址映射
设置免密登录
安装JDK
解压安装
配置jdk的环境变量 测试安装成功
分发JDK
分发配置文件
ZooKeeper配置
解压安装
添加ZK环境变量
分发文件 启动 安…
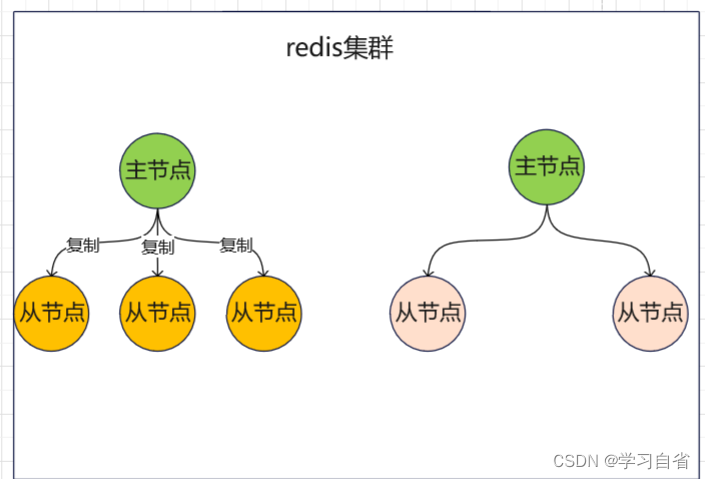
Redis基础第一篇
一 简介
redis是一个key-value存储系统。和Memcached类似,它支持存储的value类型相对更多,包括string(字符串)、list(链表)、set(集合)、zset(sorted set --有序集合)和hash(哈希类型)。这些数据类型都支持push/pop、add/remove及…
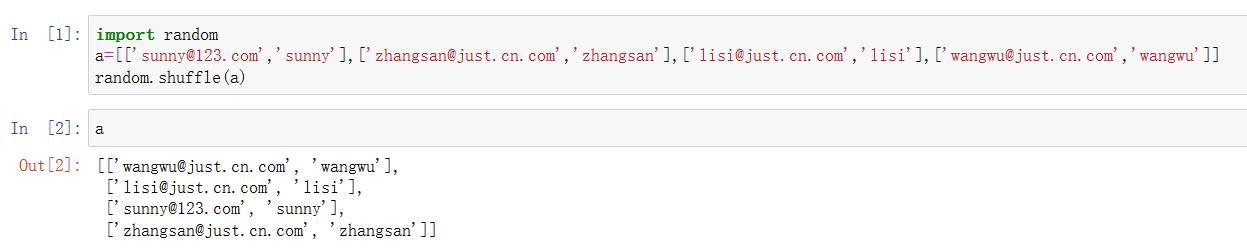
【Python基础函数笔记】random.shuffle()
官方文档:random --- 生成伪随机数 — Python 3.10.11 文档 import random
a[[sunny123.com,sunny],[zhangsanjust.cn.com,zhangsan],[lisijust.cn.com,lisi],[wangwujust.cn.com,wangwu]]
random.shuffle(a)
print(a)random.shuffle()用来打乱列表的。
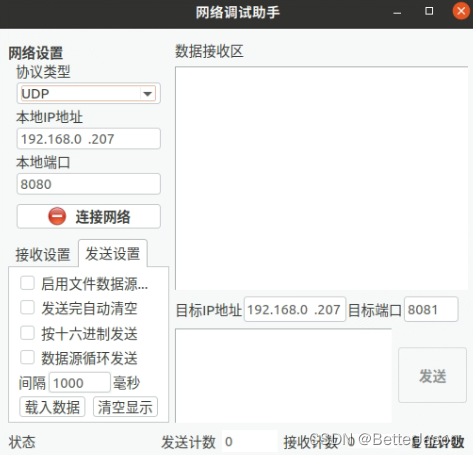
ubuntu20下安装网络调试助手
1、下载安装包
链接:https://pan.baidu.com/s/1g-IzsYBuicxiRaeo4aNyqw?pwd35wm 提取码:35wm --来自百度网盘超级会员V6的分享
2、安装依赖文件
sudo add-apt-repository ppa:rock-core/qt4
sudo apt install libqt4-declarative
3、安装网络调试工…
如何在 SOLIDWORKS 工程图中显示金折弯线?
今天我们将展示使用多种方法可以使钣金折弯线在SOLIDWORKS工程图中显示(或不显示)。
在哪里可以找到弯曲线
首先,我们需要知道弯曲线存储/创建/保存的位置。在使用钣金工具生成的零件中,折弯线存储在展开模式特征中。显示/隐藏和…
差值结构的基态和跃迁
( A, B )---3*30*2---( 1, 0 )( 0, 1 )
让网络的输入只有3个节点,AB训练集各由5张二值化的图片组成,让差值结构中有6个1, 行分布是0,1,1,2,2列分布是4,2. 得到数据 差值结构 A-B 迭代次数 共…
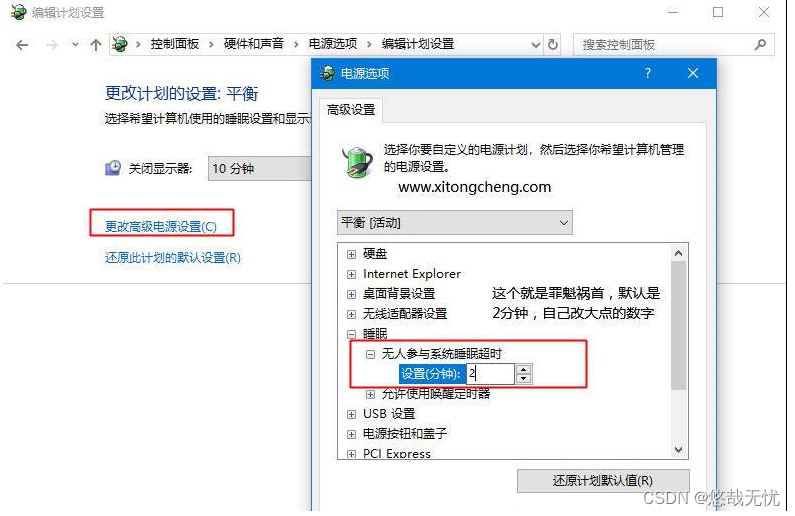
win10笔记本电脑总是自动休眠解决办法
1、运行regedit,进入注册表编辑器; 2、在打开的注册表编辑器左侧定位到:计算机\HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Control\Power\PowerSettings\238C9FA8-0AAD-41ED-83F4-97BE242C8F20\7bc4a2f9-d8fc-4469-b07b-33eb785aaca0&…
软件测试必问的十道面试题
前言
(第一个就刷掉一大批人)
有很多“会自动化”的同学来咨询技术问题,他总会问到我一些元素定位的问题。元素定位其实都不算自动化面试的问题。
一般我都会问:你是定位不到吗?通常结果都是说确实定位不到。
做自…
 构造Lagrange、Newton插值多项式,画出函数图像,并计算f(5.137)的近似值并估计误差。
构造Lagrange、Newton插值多项式,画出函数图像,并计算f(5.137)的近似值并估计误差。