目录
一些疑惑
0 引言
1 introduction
2.1 parameterization with fixed connectivity
2.2 Separate Cut Computation
3 problem statement
编辑 3.1 数学形式1
3.2 数学形式2
3.3 能量函数
3.3.1 接缝线长度(归一化),用面积归一化后,在不同数据集间具有可比性
3.3.2 变形度(基于map后的结果)
4-6 optimization framework,COUPLED DISCRETE-CONTINUOUS DESCENT,THE OPTCUTS ALGORITHM
4.1 初始状态:
4.2 外迭代:
4.2.1 lamda的迭代更新:
编辑 4.2.2 T U的迭代更新-内迭代:
7 evaluation
7.1 对比试验
一些疑惑
- (global ) bijectivity
Bijectivity 双射性 : 这样可以保证表面上的每个点都会映射到纹理空间中的不同点。如果你想让纹理在表面上重复(想想墙纸或地毯的重复图案),那么有意引入从表面点到纹理点的多对一映射是有意义的
<Chapter 11 —— Texture Mapping_五月的天气的博客-CSDN博客>
- Local injectivity <每个人都看得懂的映射(单射、满射、双射) - 知乎
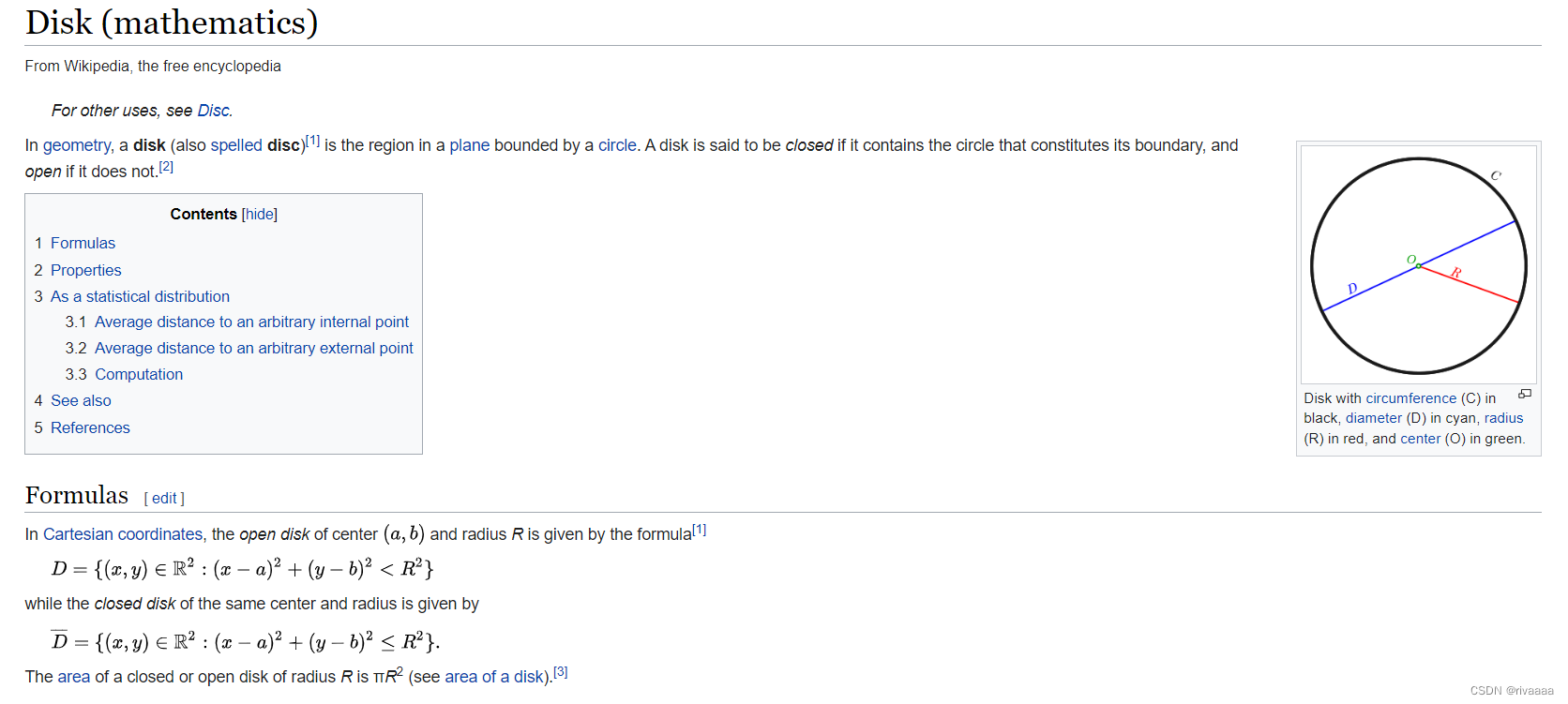
- Disk-topology:就是一个圆(open OR closed)https://en.wikipedia.org/wiki/Disk_(mathematics)
0 引言
- 作用:生成好的Uvmap 或者 优化已有的UV map(保持distortion一致的情况下)
- 接口:自定义接缝线放置 :结合语义和自定义 Hide && 保持对称性
- 关键词: mesh parameterization
1 introduction
- UV展开,两个核心问题:变形度 和 接缝线的放置问题
- 变形度和接缝线的长度二者相悖:变形度为0的时候,所有三角面片都是切割分开的
- mesh参数化(两步走):
- Geometric techniques:
- 已经cut为 disk-topology
- 需要解决的问题:将cut后的segment map到二维平面(保持固定的连接性(拓扑),最小变形)
- map过程,会改变mesh的角度和面积
- Topological
- Geometric techniques:
2 related work
- 大多数将surface cut && 最小化变形视作两个问题(sequential tasks)
- 将二者统一考虑的相关研究如下
2.1 parameterization with fixed connectivity
- 先 fixed connectivity && disk-topolgy,再优化distortion
- 不同方法,distortion metrics不同
- 常用:angular distortion
- [Aigerman and Lipman 2015; Floater 2003; Lévy et al. 2002; Sawhney and Crane 2017; She er et al. 2005],
- 其他:isometric parameterization ( account for triangle stretch)
- 评价:大多数不满足 globally bijective.
- 解决办法:初始化就满足bijective,再后续优化中阻止 local and global overlaps
- 常用:angular distortion
- 接缝线参数化
 参考:[Kharevych et al. 2006; Myles and Zorin 2013].
参考:[Kharevych et al. 2006; Myles and Zorin 2013].
- 在接缝线区域,要求参数是连续的(刚性变化相关),结果中,存在部分不连续现象
- 进一步:将接缝线放在map不连续的地方:cone singularities(锥奇点),discrete points
- 意义:对inter-surface mapping and quad meshing有效果,在storing surface signals, such as texture in atlases.效果不佳
- 其他:基于纹理的方法--倾向于接缝线长度较小
- 上述方法:先cut,再参数化【需要指定proxy metrics (各种参数阈值)】
2.2 Separate Cut Computation
- Poranne et al. [2017] proposed AutoCuts—a method
- 没有包含 bijectivity约束
- 无法指定变形的限值
- 在迭代过程中,调整用户预先指定的参数
- 用户交互(主) && 全自动两种模式,都需要用户指定namda(变形 和 接缝线长度的权重)
- 三角面片-together--影响接缝线长度
- Topology-fixed
3 problem statement
- 问题的数学思想:
 多目标优化,目标之间具有相对权重,难以确定,并且无法将权重与最终的结果对应起来,即权重没有实际意义
多目标优化,目标之间具有相对权重,难以确定,并且无法将权重与最终的结果对应起来,即权重没有实际意义- 将某个目标转换为数值约束,变为含约束条件的单目标优化问题
 3.1 数学形式1
3.1 数学形式1
- M = (V,F)
- 变量:T(topology/connectivity) = (V_T,F_T) U (position)
- 目标函数:
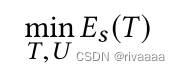
- 约束:

- V_T是V的superset:迭代过程中,顶点的数量,位置会变化,同时,3D map到2D,会产生重复的2D点
- F_T与F应该是不同的:迭代过程中,F会有所改变(拓扑改变)
- 变形度:smooth albeit nonconvex(具有多个局部最优值)
- 接缝线长度:nonsmooth
3.2 数学形式2
- 进一步,利用拉格朗日项求解含约束条件的优化问题(引入lamda变量-dual objective)约束优化的拉格朗日乘子(KKT) - 知乎 (zhihu.com)
针对lamda:变形度不满足限制时,lamda变大;变形度满足限制时,lamda 变小到0
3.3 能量函数
3.3.1 接缝线长度(归一化),用面积归一化后,在不同数据集间具有可比性
- S:在input surface(mesh)上分割后产生的所有的接缝线集合 ?? 是三维分割线,还是map到二维(考虑变形)的边界线
- ei: 接缝线长度
- F:分割后的所有面片(mesh)
- At:面片面积
3.3.2 变形度(基于map后的结果)
 参考:symmetric Dirichlet energy [Smith and Schaefer 2015]
参考:symmetric Dirichlet energy [Smith and Schaefer 2015]
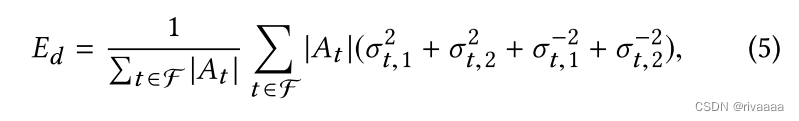
sigma为变形梯度的singular value
- distortion energy的额外项:--大部分同autoCut
- 本文:采用scaffolding method of Jiang et al. [2017] --实现 global bijective,优先三角化 outer, air-mesh in void regions
- distortion energy 增加了额外项,但不包含在计算变形度中(与优化过程有关,影响优化方向,但是不包含在计算distortion)
- not included in the distortion bound constraint,防止void-sapce 三角面片造成能量函数奔溃
- why:相对于autoCut改进
考虑基于negative-space triangles的拓扑操作
具体为:
- triangulate the void region about the union of one rings around the participating stencil vertices. This provides a sufficient scaffold to ensure bijectivity in the local solve without growing the problem size.
- for each candidate edge split we need to carefully pull apart the new split vertices to form an initial void to build the scaffold triangulation
4-6 optimization framework,COUPLED DISCRETE-CONTINUOUS DESCENT,THE OPTCUTS ALGORITHM

4.1 初始状态:
- lamda_0 =0
- T_0,U_0:先确定初始seam,再最小化distortion 得到T_0,U_0
- 初始Seam:
- 本文:circle , map过程中,保证边的长度不变preserving edge lengths
- Disk-topology surface: longest boundary
- Genus-0 closed surface: randomly tow connected edges
- Higher-genus: homology generators (using the cut_to_disk function in libigl -同autoCut)
- 其他方法:在后续实验有使用另一种初始化方式:initialization from scratch [I.e., directly starting from the Tutte embedding of each mesh.]
- 本文:circle , map过程中,保证边的长度不变preserving edge lengths
- 顶点参数化(包含在最小化distortion):
- Tutte’s embedding [1963] using uniform weights to ensure bijectivity
- William Thomas Tutte. 1963. How to draw a graph. Proceedings ofthe London Mathematical Society 3, 1 (1963), 743–767.
4.2 外迭代:
- 在主变量 T U 和dual 变量 lamda之间交替优化,交替时,非优化对象,视作常量;外迭代中一次主变量 T U的更新,包含多次内迭代
- 外迭代终止条件(未限定最大迭代数):
- 内迭代收敛终止 &&
- lamda上收敛

- cyclic stationarity condition (伪代码中没有包含)--简要概括:外迭代可行解复现
Ps:当前连续的topology变化,可能不是最优方案
离散的拓扑变化需要被考虑,因此在内迭代过程中,非连续的topology变化,可根据是否被再次搜索到,来决定其是否是可行解
save hashes (Es , Ed, lamda) of solution triplets, and the best visited solution,of solution triplets, and the best visited solution
4.2.1 lamda的迭代更新:
- lamda的变化是 nonsmooth:根据E_d & E_d_th 变化(非平滑):
-




Ed<bd

-
- 改进:给拉格朗日项增加一个关于lamda的quadratic 二次正则化项,使得lamda变化 smooth(数学原理参考其他--称作“增加不等式约束,使得lamda变化smooth”)

-
Ps: Smooth:新的lamda与原lamda相似
-
- lamda最终更新方式
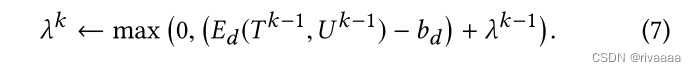
 4.2.2 T U的迭代更新-内迭代:
4.2.2 T U的迭代更新-内迭代:
- 是一个(T-)离散 && (U-)连续的变量交替优化过程(交替时,非优化对象,视作常量)
- 内迭代终止条件
- topology变化相对于朗格朗日项(等效理解为总的能量函数)收敛

- 当前topology,使得distortion足够小
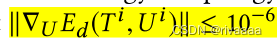
- topology变化相对于朗格朗日项(等效理解为总的能量函数)收敛
4.2.2.1 T的优化
- autoCut:
- 拓扑变化有限(即最后将seperation 较小的corner合并)
- 不适合本文:larger mesh(strongly ill-conditioned real-valued optimization and prevented scaling to larger meshes)
- 本文方法:(核心点)T的可行解搜索是一个”化离散为连续 “的方式 Ps: 常规方式:穷举遍历搜索可行解
- 本文:
- 离散变量,局部搜索迭代(等效为连续变化) delta_T,根据一定的原则确定更新后的T:
- 针对topology的局部搜索:基于当前的拓扑,相似的/微小 的拓扑变化(cutting && merging组合)---delta_Tology
- delta_Tology计算:cutting && merging:共三种,组合&&选择生成可行解
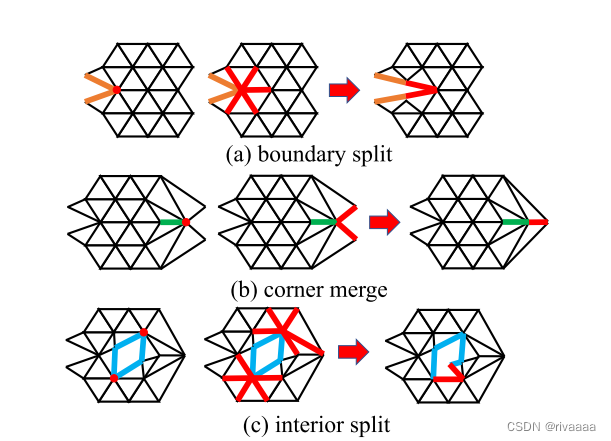
- 三种基本拓扑变化
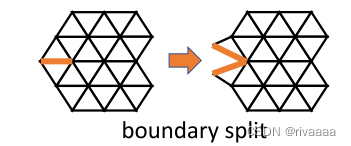
- Boundary vertex split:产生2/4(橙色的边链接另一个边界顶点的情形)个重复顶点
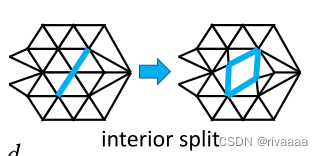
- Interior vertex split:产生2个重复顶点
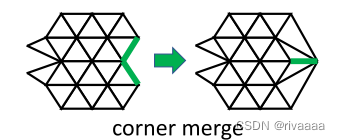
- Corner merge:合并后顶点的位置-average(中点),而不是Naïve merging--违背local injectivity;合并后,若出现inversion(三角面片有向面积为负,顶点顺序),用Agmon’s relaxation 解决,若不能解决,放弃这种mesh 操作i
- Boundary vertex split:产生2/4(橙色的边链接另一个边界顶点的情形)个重复顶点
- 选择策略:
- 首先boundary:
- 选择subset of 边界顶点:顶点的优先级,由相对于distortion energy 梯度的标准差的偏差决定,偏差越大,优先选择
- cutting这些顶点能极大的去除这些大偏差,有助于降低变形度
- 基于boundary,考虑所有的seams的corner merging操作,共同构成一个操作集合
- 计算distortion降低的值,得到最佳方案;若所有操作都不能使d降低,最后考虑interior
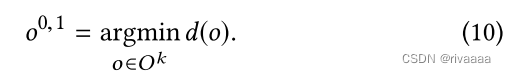
- 考虑interior:选择部分内部顶点(选择规则同边界顶点),同上在构成的操作集合中,得到使d降低的最终方案
- 下一次的内迭代的拓扑变化,从由拓展(propagation)上一次的拓扑变化得到的操作集合中选择,因此O_01格外重要
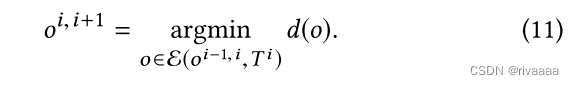
- 首先boundary:
- 如何根据delta_T 计算更新后的T
- 核心:要么接受delta_T,直接更新,要么拒绝delta_T,T保持不变
- 接受/拒绝的原则1:为了减少拓扑变化过程中顶点节点的变化,内迭代中,某次拓扑结构变化,使得d满足阈值,就更新内迭代T,否则T不更新;

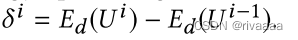
- 阈值:初始为0,后续会变化
- 接受/拒绝的原则2:拉格朗日项是否降低,且尽可能降低得多(类似于评估是否为优化拉格朗日项的迭代方向)
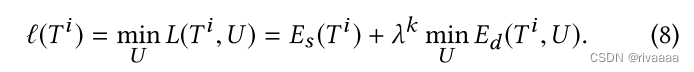

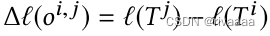
- 由于,关于mesh的topology更新O_ij,会引起U的变化(U_ij表示因O_ij而受影响的顶点集合,尽可能减少顶点的改变,U_S表示不受影响的顶点集合),因此,上述delta_l的形式为:
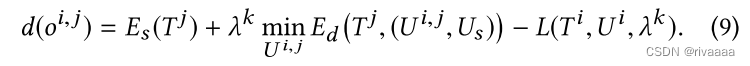
- 由于,关于mesh的topology更新O_ij,会引起U的变化(U_ij表示因O_ij而受影响的顶点集合,尽可能减少顶点的改变,U_S表示不受影响的顶点集合),因此,上述delta_l的形式为:
4.2.2.2 U优化
- Newton法,梯度下降,线性搜索
- 由于distorton E nonconvex,进一步采用 projected-Newton(Hessian),保证PSD--采用TBB 并行化线性搜索过程
- 关于U有优化过程中,考虑distortion最小化要求时,根据T迭代是否满足要求来确定
若更新内迭代T,则最小化要求较严格;若T不更新,该要求较宽松
7 evaluation
- 数据:benchmark mesh dataset
- 71model
- 80-10k 顶点,ave: 3.7
- 参数:bd : {4.2, 4.1, 4.05}.
- 指标,Es、 Ed、 运行时间(最大、小值,平均值)
7.1 对比试验
| 实验类型 | 结论 |
| Global bijectivity VS local injectivity | Global bijectivity约束强:时间的多,seam长 |
| optCut VS autoCut(自动模式) | 整体上:optCut 时间短,展开线短 |
| 进一步讨论Scalability(顶点数) 对时间的影响 | 顶点数越多,时间差异越大; 耗时: optCut(无bijectivity约束)>optCut(有bijectivity约束)> autoCut 24k and 48k数据:autoCut(复制所有的顶点),out of memory |
| 比较topology operation: 本文:local ——减少计算开销 其他:Geometry Images [Gu et al. 2002] - EB(extrema-to-boundary) cuts:connect the current boundary to the most distored point | EB(extrema-to-boundary) cuts: 收敛较慢,展开线更长 EB在下述情况,收敛较快,但展开线更长:isometric(等距、等角) UV maps where extremities are less prominent(极端/末端不突出) |
| optCut VS autoCut(交互模式)VS Sorkine et al. [2002](Bounded distortion piecewise mesh parameterization) | |
| optCut VS Unwrella2, ZBrush3, and Maya4,
| hard-surface mode occasionally produced UV meshes with local inversions and non-manifold vertices 解决办法:organic mode Unwrella、Maya distortion的优化可能较宽松,因此:Unwrella、Maya结果的基础上,在seam不变的情况下,利用optCut再次最小化distortion得到最终结果,再与原始optCut对比
|
7.2 讨论展开线的位置:Regional Seam Placement
- 远离显著区域:salient surface regions
- 方法:给显著区域surface加一个权重,用以惩罚seam length——权重越大,”length越长“
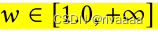
- 改进后的E_s

- 输入:salience map(w越大,显著性越强 w = 1~100):Salience map的格式到底是什么?是基于三维面片标注,还是基于二维展开标注
- 最后的最优解可能与无salience map情况不同,可能会更优,即权值w可能帮助跳出局部最优解

7.3 optCut的另一个应用:优化现有UV展开结果
- 实验:
- 初始值:Seamster [She er and Hart 2002] ——检测局部曲率极值,并采用 MST进行连接;
- Seamster [She er and Hart 2002] 对输入的参数敏感(size of surface regions——与模型的形状有关,不同模型,需要调整该参数
8 conclusion
- 优化收敛性:尽管都收敛了(固定阈值 or 最优解cyclical recall,非启发式阈值)——但无法证明一定会收敛
- 满足distortion阈值的前提下,seam length 可能是个局部解
- 增加顶点位置扰动,可能帮助跳出局部解,得到distortion 更小的解
- 提速的要点:
- 拓扑操作,可以并行化
- 线性搜索是可以分解的
- 其他可能的改进:
- favor seamless parameterization,
- seam smoothness,
- the creation of charts that effciently use texture space.


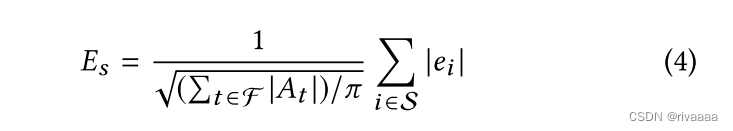



![[附源码]计算机毕业设计JAVA职业中介信息管理系统](https://img-blog.csdnimg.cn/2b3f232d33104d79a56a78944b518b73.png)