一、初始相角的位移量

在信号处理中正弦信号经常表示为 $x\left( n \right)=A\cos (2\pi {{f}_{0}}n/{{f}_{s}}+\theta )$ ，其中 ${{f}_{s}}$ 是采样频率， ${{f}_{0}}$ 是正弦信号的频率，A是信号的幅值，θ是信号的初始相角。而初始相角值也相当于一个时间的位移量。

信号可进一步表示为：

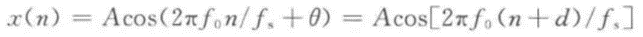
在这里插入图片描述
由上式可知

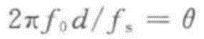
在这里插入图片描述

然后导出

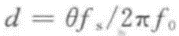
在这里插入图片描述
d值就是所要求的相角代表的位移样点量。

而要使信号恢复到初始相角为0，则相当于要设置一个函数y(n)，满足y(n)=x(n-d)，可得到

在这里插入图片描述

二、获取原始信号的振幅与初始相位角

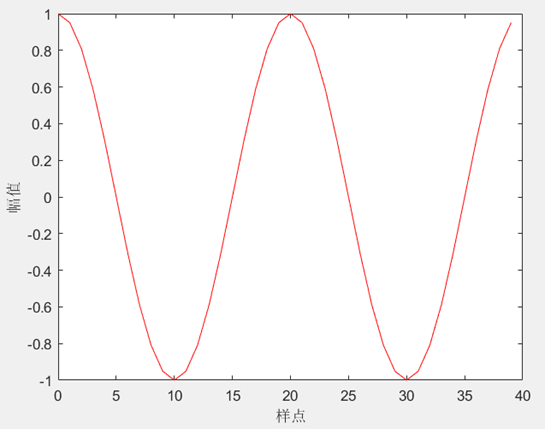
假如有一正弦信号，如下图所示：

Matlab代码如下：

%% 原始信号
fs = 2000;                      % 采样频率
N = 40;                         % 信号长度
n = 0:N-1;                      % 样点序列
f0 = 100;                       % 初始频率
ph1=-pi/3;                      % 初始相角
x=cos(2*pi*f0*n/fs+ph1);        % 余弦信号序列
figure,plot(n,x,'r')
xlabel('样点'); ylabel('幅值');

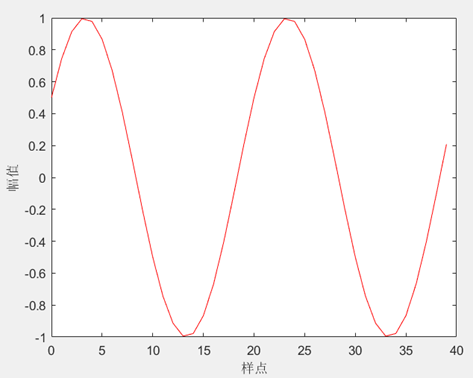
在这里插入图片描述

图1 正弦信号

通过对上述信号进行傅里叶变换，得到频域谱，可通过分析获得信号在频域谱上的位置值，利用该位置，即可计算出上述信号的幅值与初始相位角，对应的Matlab代码如下：

%% 通过FFT计算信号幅值和信号初始相位角
X=fft(x);                      % FFT
figure,plot(n,real(X),'r');title('信号的频域图')
df = fs/N;                      % 计算频率间隔
nk=f0/df+1;                     % 信号在nk谱线上
A=abs(X(nk))*2/N;               % 计算幅值
Theta=angle(X(nk));             % 计算初始相角

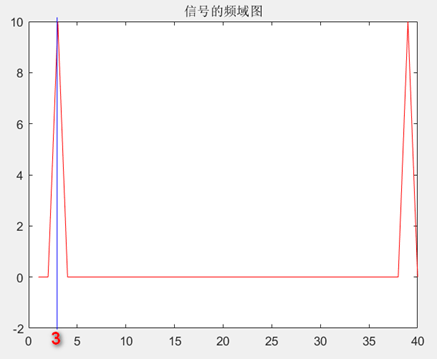
在这里插入图片描述

图2 信号频谱

此时，计算出的信号幅值为1和初始相位角为-1.0472，因此，通过傅里叶变换后计算得到的信号幅值和初始相位角与设置值完全一致。

三、相角位移量计算与信号恢复到初始相角为0

对于本例来说，初始相角值ph1为负值，对应的样点值d也为负值，波形又要左移。
此时，根据上述理论公式，计算得到的相角位移量d=-3.33333

对应的Matlab代码如下：

%% 相角位移量计算
d = ph1*fs/f0/(2*pi);           % 计算位移量

根据第一节的理论，使原始信号位移，此时恢复得到的信号如下图所示：

在这里插入图片描述

图3 信号发生位移(此时初相角为0)

计算得到初始相位角为0。

对应的matlab代码如下：

%% 信号恢复到初始相角为0
Ex=exp(-1j*2*pi*n*d/N);         % 计算旋转因子W^(dk) 

Y = X.*Ex;                      % FFT后乘旋转因子
figure,plot(n,real(Y),'r');title('信号的频域图')

y=ifft(Y);                      % FFT逆变换
y1=real(y);                     % 取的实部
figure,plot(n,y1,'r')
xlabel('样点'); ylabel('幅值'); 

Y1=fft(y1);                     % FFT
df = fs/N;                      % 计算频率间隔
nk=f0/df+1;                     % 信号在nk谱线上
A=abs(real(Y1(nk)))*2/N;        % 计算幅值
Theta=angle(Y1(nk));            % 计算初始相角