【力扣】前缀和/滑动窗口：209. 长度最小的子数组

1. 问题

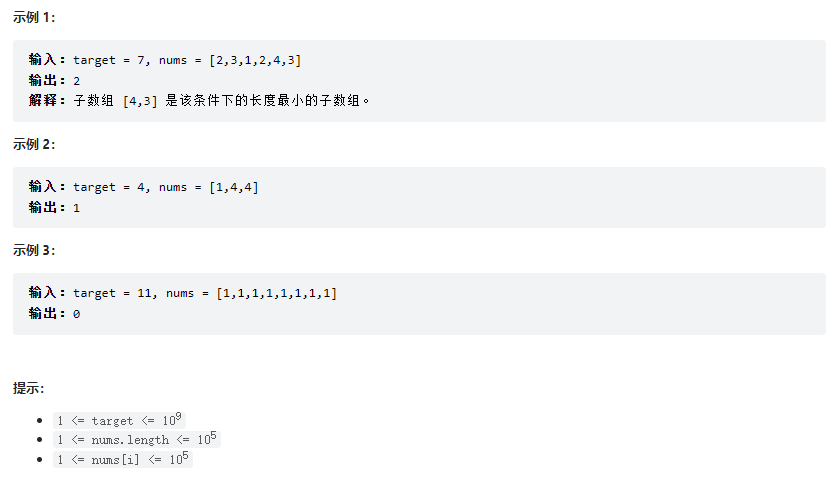
给定一个含有 n 个正整数的数组和一个正整数 target 。

• 找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 $[num{s}_l,num{s}_{l+1},...,num{s}_{r-1},num{s}_r]$，并返回其长度。
• 如果不存在符合条件的子数组，返回 0 。
  

2. 题解

2.1 暴力法

• 二重循环，每一个区间都遍历一遍。

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int n = nums.size();
        if (n == 0) {
            return 0;
        }
        int ans = 100001;
        for (int i = 0; i < n; i++) {
            int sum = 0;
            for (int j = i; j < n; j++) {
                sum += nums[j];
                if (sum >= s) {
                    ans = min(ans, j - i + 1);
                    break;
                }
            }
        }
        return ans == 100001 ? 0 : ans;
    }
};

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

2.2 前缀和 + 二分查找

• 暴力法确定每个子数组的开始下标后，找到长度最小的子数组需要 O(n) 的时间。如果使用二分查找，则可以将时间优化到 O(logn)。
• 使用二分查找，需要额外创建一个数组 sums 用于存储数组 nums 的前缀和。

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int n = nums.size();
        if (n == 0) {
            return 0;
        }
        int ans = 100001;
        vector<int> sums(n + 1, 0); 
        for (int i = 1; i <= n; i++) {
            sums[i] = sums[i - 1] + nums[i - 1];
        }
        for (int i = 1; i <= n; i++) {
            int target = s + sums[i - 1];
            auto bound = lower_bound(sums.begin(), sums.end(), target);
            if (bound != sums.end()) {
                ans = min(ans, static_cast<int>((bound - sums.begin()) - (i - 1)));
            }
        }
        return ans == 100001 ? 0 : ans;
    }
};

• 时间复杂度：$O(nlogn)$
• 空间复杂度：$O(n)$

2.3 滑动窗口

• 定义两个指针分别表示子数组（滑动窗口窗口）的开始位置和结束位置。

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int n = nums.size();
        if (n == 0) {
            return 0;
        }
        int ans = 100001;
        int start = 0, end = 0;
        int sum = 0;
        while (end < n) {
            sum += nums[end];
            while (sum >= s) {
                ans = min(ans, end - start + 1);
                sum -= nums[start];
                start++;
            }
            end++;
        }
        return ans == 100001 ? 0 : ans;
    }
};

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

参考

【1】https://leetcode.cn/problems/minimum-size-subarray-sum
【2】https://leetcode.cn/problems/minimum-size-subarray-sum/solution/chang-du-zui-xiao-de-zi-shu-zu-by-leetcode-solutio/