🌞欢迎来到深度学习的世界
🌈博客主页:卿云阁💌欢迎关注🎉点赞👍收藏⭐️留言📝
🌟本文由卿云阁原创!
🙏作者水平很有限,如果发现错误,请留言轰炸哦!万分感谢!
目录
4.1 从数据中学习
4.2 损失函数
4.3 数值微分
4.5 学习算法的实现
4.1 从数据中学习
4.1.1 数据驱动
4.1.2 训练数据和测试数据
机器学习中,一般将数据分为 训练数据 和 测试数据 两部分来进行学习和实验等。首先,使用训练数据进行学习,寻找最优的参数;然后,使用测试数据评价训练得到的模型的实际能力。为什么需要将数据分为训练数据和测试数据呢?因为我们追求的是模型的泛化能力。为了正确评价模型的泛化能 力,就必须划分训练数据和测试数据。泛化能力是指处理未被观察过的数据(不包含在训练数据中的数据)的 能力。 只对某个数据集过度拟合的状态称为过拟合(over fitting )。避免过拟合也是机器学习的一个重要课题。4.2 损失函数
假设我现在有一个检测任务,目的是为了检测出图像中有没有小狗。一个彩色的图像有3个通道。 灰度图片:在灰色图中会把每一个像素用0-255之间的数字表示,越接近白色,数字越接近255。RGB彩色图片:RGB色彩模式也就是红(Red)、绿(Green)、蓝(Blue)色彩模式。指的是通过R、G、B三个色彩通道,它们相互叠加再得到各式各样的颜色。它们的范围都是0~255,这样叠加起来就能够得到256*256*256=16777216(大约1678w)的颜色种类。一张有颜色的图像由一个三维数组表示。因此,要表示彩色值,我们需要3个维度,也就是3个图像通道,每个像素值用3个数字表示,如(255,255,255)表示白色,(255,0,0)表示红色,(255,255,0)表示黄色。此时我们可以设置一个阈值,当输出结果>0.8时可以认为图片上是有小狗的。
此是y的值是0.9,如何衡量我预测结果的好坏呐。这个时候就要引入损失函数了。
loss=h(|y-y1|),y表示预测值,y1表示真实值。损失函数有很多中。
4.2.1 均方误差
可以用作损失函数的函数有很多,其中最有名的是 均方误差 ( mean squared error)。均方误差如下式所示。
这里,yk是表示神经网络的输出,tk表示监督数据,k表示数据的维数。 比如,在3.6节手写数字识别的例子中,yk、tk是由如下10个元素构成的数据。
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0] t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]这里,神经网络的输出y 是 softmax 函数的输出。由于 softmax 函数的输出可以理解为概率,因此上例表示“0”的概率是0 . 1 等。t 是监督数据, 表示正确解是“2”。将正确解标签表示为 1 ,其他标签表示为 0 的表示方法称为one-hot表示。均方误差显示第一个例子的输出结果与监督数据更加吻合。def mean_squared_error(y, t): return 0.5 * np.sum((y-t)**2) #真实标签 t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0] #预测标签y1 y1 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0] #预测标签y2 y2 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0] #计算损失值 print("-----损失值1-----") print("损失值1:={0}".format(mean_squared_error(np.array(y1), np.array(t)))) print("-----损失值2-----") print("损失值2={0}".format(mean_squared_error(np.array(y2), np.array(t))))
4.2.2 交叉熵误差
除了均方误差之外, 交叉熵误差 ( cross entropy error )也经常被用作损 失函数。交叉熵误差如下式所示。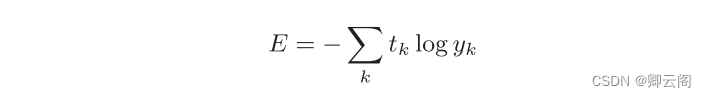 y k 是神经网络的输出, t k 是正确解标签。并且, t k 中只有正确解标签的索引为 1 ,其他均为 0 ( one-hot 表示)。 因此, 实际上只计算对应正确解标签的输出的自然对数。比如,假设正确解标签的索引是“2”,与之对应的神经网络的输出是 0 . 6 ,则交叉熵误差 是− log 0 . 6 = 0 . 51 ;若“2”对应的输出是 0 . 1 ,则交叉熵误差为 − log 0 . 1 = 2 . 30 。 也就是说,交叉熵误差的值是由正确解标签所对应的输出结果决定的。自然对数的图像如图所示
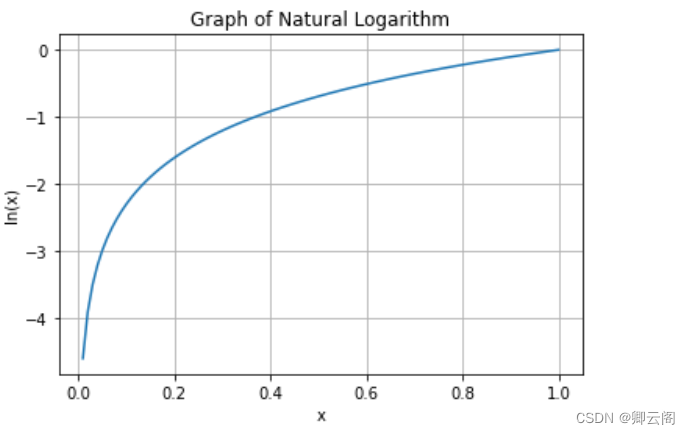
y k 是神经网络的输出, t k 是正确解标签。并且, t k 中只有正确解标签的索引为 1 ,其他均为 0 ( one-hot 表示)。 因此, 实际上只计算对应正确解标签的输出的自然对数。比如,假设正确解标签的索引是“2”,与之对应的神经网络的输出是 0 . 6 ,则交叉熵误差 是− log 0 . 6 = 0 . 51 ;若“2”对应的输出是 0 . 1 ,则交叉熵误差为 − log 0 . 1 = 2 . 30 。 也就是说,交叉熵误差的值是由正确解标签所对应的输出结果决定的。自然对数的图像如图所示#自然对数的图像 import numpy as np import matplotlib.pyplot as plt # 生成自变量x的取值范围 x = np.linspace(0.1, 10, 100) # 计算自然对数的函数值 y = np.log(x) # 绘制图像 plt.plot(x, y) plt.xlabel('x') plt.ylabel('ln(x)') plt.title('Graph of Natural Logarithm') plt.grid(True) plt.show()
x 等于 1 时, y 为 0 ;随着 x 向 0 靠近, y 逐渐变小。因此, 正确解标签对应的输出越大,值越接近0 ;当输出为 1 时,交叉熵 误差为0。此外,如果正确解标签对应的输出较小,值较大。#交叉熵误差 def cross_entropy_error(y, t): delta = 1e-7 return -np.sum(t * np.log(y + delta)) #真实标签 t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0] #预测标签y1 y1 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0] #预测标签y2 y2 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0] #计算损失值 print("-----损失值1-----") print("损失值1={0}".format(cross_entropy_error(np.array(y1), np.array(t)))) print("-----损失值2-----") print("损失值2={0}".format(cross_entropy_error(np.array(y2), np.array(t))))
参数 y 和 t 是 NumPy 数组。函数内部在计算 np.log 时,加上了一 个微小值delta 。这是因为,当出现 np.log(0) 时, np.log(0)会变为负无限大 的-inf,这样一来就会导致后续计算无法进行。作为保护性对策,添加一个 微小值可以防止负无限大的发生。 第一个例子中,正确解标签对应的输出为 0 . 6 ,此时的交叉熵误差大约 为 0 . 51 。第二个例子中,正确解标签对应的输出为 0 .1 的低值,此时的交叉 熵误差大约为 2 . 3 。由此可以看出,这些结果与我们前面讨论的内容是一致的。4.2.3 mini-batch学习
计算损失函数时必须将所有的训练数据作为对象。也就是说,如果训练数据有100 个的话,我们就要把这100个损失函数的总和作为学习的指标。 前面介绍的损失函数的例子中考虑的都是针对单个数据的损失函数。如果要求所有训练数据的损失函数的总和,以交叉熵误差为例,可以写成下面的式子。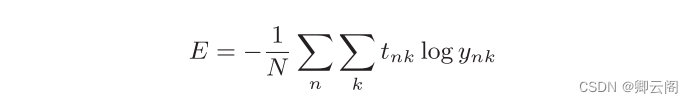 这里 , 假设数据有 N 个, t nk 表示第 n 个数据的第 k 个元素的值( y nk 是神经网络的输出,t nk 是监督数据)。式子虽然看起来有一些复杂,其实只是把 求单个数据的损失函数的式扩大到了N 份数据,不过最后还要除以 N进行正规化。通过除以N ,可以求单个数据的“平均损失函数”。通过这样的平均化,可以获得和训练数据的数量无关的统一指标。比如,即便训练数据有 1000 个或 10000 个,也可以求得单个数据的平均损失函数。另外, MNIST 数据集的训练数据有 60000 个,如果以全部数据为对象求损失函数的和,则计算过程需要花费较长的时间。再者,如果遇到大数据,数据量会有几百万、几千万之多,这种情况下以全部数据为对象计算损失函 数是不现实的。因此,我们从全部数据中选出一部分,作为全部数据的“近似”。神经网络的学习也是从训练数据中选出一批数据(称为mini-batch , 小批量),然后对每个mini-batch 进行学习。比如,从 60000 个训练数据中随机选择 100个 ,再用这 100个 数据进行学习。这种学习方式称为 mini-batch 学习 。 下面我们来编写从训练数据中随机选择指定个数的数据的代码,以进行 mini-batch学习。在这之前,先来看一下用于读入 MNIST 数据集的代码。
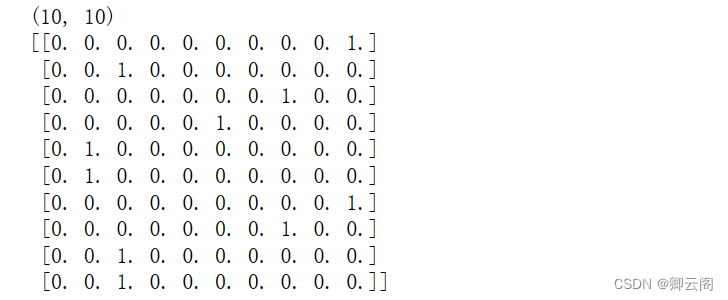
这里 , 假设数据有 N 个, t nk 表示第 n 个数据的第 k 个元素的值( y nk 是神经网络的输出,t nk 是监督数据)。式子虽然看起来有一些复杂,其实只是把 求单个数据的损失函数的式扩大到了N 份数据,不过最后还要除以 N进行正规化。通过除以N ,可以求单个数据的“平均损失函数”。通过这样的平均化,可以获得和训练数据的数量无关的统一指标。比如,即便训练数据有 1000 个或 10000 个,也可以求得单个数据的平均损失函数。另外, MNIST 数据集的训练数据有 60000 个,如果以全部数据为对象求损失函数的和,则计算过程需要花费较长的时间。再者,如果遇到大数据,数据量会有几百万、几千万之多,这种情况下以全部数据为对象计算损失函 数是不现实的。因此,我们从全部数据中选出一部分,作为全部数据的“近似”。神经网络的学习也是从训练数据中选出一批数据(称为mini-batch , 小批量),然后对每个mini-batch 进行学习。比如,从 60000 个训练数据中随机选择 100个 ,再用这 100个 数据进行学习。这种学习方式称为 mini-batch 学习 。 下面我们来编写从训练数据中随机选择指定个数的数据的代码,以进行 mini-batch学习。在这之前,先来看一下用于读入 MNIST 数据集的代码。import sys, os sys.path.append(os.pardir) import numpy as np from dataset.mnist import load_mnist (x_train, t_train), (x_test, t_test) = \ load_mnist(normalize=True, one_hot_label=True) print(x_train.shape) # (60000, 784) print(t_train.shape) # (60000, 10)那么,如何从这个训练数据中随机抽取10笔数据呢?我们可以使用NumPy的np.random.choice() ,写成如下形式。#x_train.shape[0]是60000 train_size = x_train.shape[0] batch_size = 10 batch_mask = np.random.choice(train_size, batch_size) x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] #t_batch print(t_batch.shape) print(t_batch)
使用 np.random.choice() 可以从指定的数字中随机选择想要的数字。比如, np.random.choice(60000, 10)会从 0 到 59999 之间随机选择 10 个数字。如下面的实际代码所示,我们可以得到一个包含被选数据的索引的数组。
4.2.4 mini-batch版交叉熵误差的实现
#NumPy数组的size属性获取元素数量 #并使用reshape方法将数组重新组织为形状为(1, 10)的二维数组。最后,打印重塑后的t和y数组。 t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0] y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0] t = np.array(t) y = np.array(y) print(t.size) print(t.shape) t = t.reshape(1, t.size) print(t) y = y.reshape(1, y.size) print(y) 这里,我们来实现一个可以同时处理单个数据和批量数据(数据作为batch 集中输入)两种情况的函数。
这里,我们来实现一个可以同时处理单个数据和批量数据(数据作为batch 集中输入)两种情况的函数。def cross_entropy_error(y, t): #y是真实的标签,如果y的维度是1,说明是计算单个数据的 t = np.array(t) y = np.array(y) if y.ndim == 1: t = t.reshape(1, t.size) print(t) y = y.reshape(1, y.size) print(y) batch_size = y.shape[0] return -np.sum(t * np.log(y + 1e-7)) / batch_size t1 = [[0, 0, 1, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 1, 0]] y1 = [[0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0], [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]] #真实标签 t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0] #预测标签y1 y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0] #单个数据 #计算损失值 print("-----损失值1-----") print("损失值1={0}".format(cross_entropy_error(np.array(y), np.array(t)))) print("-----损失值2-----") print("损失值2={0}".format(cross_entropy_error(np.array(y1), np.array(t1)))) y 是神经网络的输出, t 是监督数据。 y 的维度为 1 时,即求单个数据的交叉熵误差时,需要改变数据的形状。并且,当输入为mini-batch 时, 要用batch 的个数进行正规化,计算单个数据的平均交叉熵误差。此外,当监督数据是标签形式(非 one-hot 表示,而是像“ 2 ”“ 7 ”这样的 标签)时,交叉熵误差可通过如下代码实现。
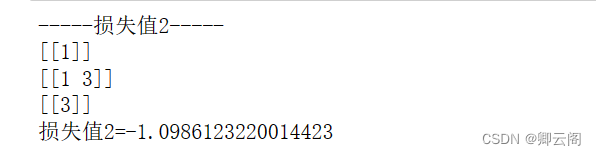
y 是神经网络的输出, t 是监督数据。 y 的维度为 1 时,即求单个数据的交叉熵误差时,需要改变数据的形状。并且,当输入为mini-batch 时, 要用batch 的个数进行正规化,计算单个数据的平均交叉熵误差。此外,当监督数据是标签形式(非 one-hot 表示,而是像“ 2 ”“ 7 ”这样的 标签)时,交叉熵误差可通过如下代码实现。def cross_entropy_error(y, t): #y是真实的标签,如果y的维度是1,说明是计算单个数据的 if y.ndim == 1: t = t.reshape(1, t.size) print(t) y = y.reshape(1, y.size) print(y) batch_size = y.shape[0] print(y[np.arange(batch_size), t]) return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size t1 = [1] y1 = [1,3] #真实标签 #单个数据 #计算损失值 print("-----损失值2-----") print("损失值2={0}".format(cross_entropy_error(np.array(y1), np.array(t1))))
实现的要点是,由于 one-hot 表示中 t 为 0 的元素的交叉熵误差也为 0 ,因此针对这些元素的计算可以忽略。换言之,如果可以获得神经网络在正确解标签处的输出,就可以计算交叉熵误差。因此,t 为 one-hot 表示时通过t * np.log(y)计算的地方,在 t 为标签形式时,可用 np.log( y[np.arange (batch_size), t] )实现相同的处理(为了便于观察,这里省略了微小值 1e-7 )。作为参考,简单介绍一下 np.log( y[np.arange(batch_size), t] ) 。 np.arange (batch_size)会生成一个从 0到batch_size-1 的数组。比如当 batch_size为5 时, np.arange(batch_size) 会生成一个 NumPy 数组 [0, 1, 2, 3, 4]。因为t中标签是以 [2, 7, 0, 9, 4] 的形式存储的,所以 y[np.arange(batch_size), t]能抽出各个数据的正确解标签对应的神经网络的输出(在这个例子中, y[np.arange(batch_size), t] 会生成 NumPy 数 组 [y[0,2], y[1,7], y[2,0],y[3,9], y[4,4]] )。4.2.5 为何要设定损失函数
上面我们讨论了损失函数,可能有人要问:“为什么要导入损失函数呢?” 以数字识别任务为例,,既然我们的目标是获得使识别精度尽可能高的神经网络,那不是应该把识别精度作为指标吗?对于这一疑问,我们可以根据“导数”在神经网络学习中的作用来回答。 下一节中会详细说到,在神经网络的学习中,寻找最优参数(权重和偏置)时, 要寻找使损失函数的值尽可能小的参数。为了找到使损失函数的值尽可能小的地方,需要计算参数的导数(确切地讲是梯度),然后以这个导数为指引, 逐步更新参数的值。假设有一个神经网络,现在我们来关注这个神经网络中的某一个权重参数。此时,对该权重参数的损失函数求导,表示的是“如果稍微改变这个权 重参数的值,损失函数的值会如何变化”。如果导数的值为负,通过使该权重参数向正方向改变,可以减小损失函数的值;反过来,如果导数的值为正, 则通过使该权重参数向负方向改变,可以减小损失函数的值。不过,当导数 的值为0 时,无论权重参数向哪个方向变化,损失函数的值都不会改变,此时该权重参数的更新会停在此处。之所以不能用识别精度作为指标,是因为这样一来绝大多数地方的导数都会变为0 ,导致参数无法更新。话说得有点多了,我们来总结一下上面的内容。 在进行神经网络的学习时,不能将识别精度作为指标。因为如果以识别精度为指标,则参数的导数在绝大多数地方都会变为0 。 为什么用识别精度作为指标时,参数的导数在绝大多数地方都会变成0呢?为了回答这个问题,我们来思考另一个具体例子。假设某个神经网络正确识别出了100 笔训练数据中的 32 笔,此时识别精度为 32 % 。如果以识别精 度为指标,即使稍微改变权重参数的值,识别精度也仍将保持在32 % ,不会出现变化。也就是说,仅仅微调参数,是无法改善识别精度的。即便识别精度有所改善,它的值也不会像32 . 0123 ... % 这样连续变化,而是变为 33 % 、 34 %这样的不连续的、离散的值。而如果把损失函数作为指标,则当前损失函数的值可以表示为0 . 92543 ... 这样的值。并且,如果稍微改变一下参数的值,对应的损失函数也会像0 . 93432 ... 这样发生连续性的变化。 识别精度对微小的参数变化基本上没有什么反应,即便有反应,它的值 也是不连续地、突然地变化。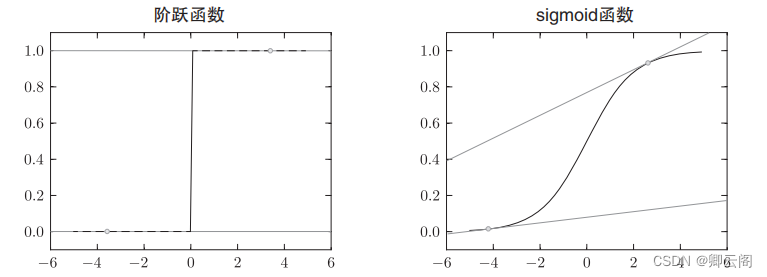 作为激活函数的阶跃函数也有同样的情况。出于相同的原因,如果使用阶跃函数作为激活函数,神经网络的学习将无法进行。 阶跃函数的导数在绝大多数地方(除了0 以外的地方)均为 0 。 也就是说,如果使用了阶跃函数,那么即便将损失函数作为指标,参数的微小变化也会被阶跃函数抹杀,导致损失函数的值不会产生任何变化。 阶跃函数就像“竹筒敲石”一样,只在某个瞬间产生变化。而sigmoid 函数, 不仅函数的输出(竖轴的值)是连续变化的,曲线的斜率(导数) 也是连续变化的。也就是说,sigmoid 函数的导数在任何地方都不为 0 。这对 神经网络的学习非常重要。得益于这个斜率不会为0 的性质,神经网络的学习得以正确进行。
作为激活函数的阶跃函数也有同样的情况。出于相同的原因,如果使用阶跃函数作为激活函数,神经网络的学习将无法进行。 阶跃函数的导数在绝大多数地方(除了0 以外的地方)均为 0 。 也就是说,如果使用了阶跃函数,那么即便将损失函数作为指标,参数的微小变化也会被阶跃函数抹杀,导致损失函数的值不会产生任何变化。 阶跃函数就像“竹筒敲石”一样,只在某个瞬间产生变化。而sigmoid 函数, 不仅函数的输出(竖轴的值)是连续变化的,曲线的斜率(导数) 也是连续变化的。也就是说,sigmoid 函数的导数在任何地方都不为 0 。这对 神经网络的学习非常重要。得益于这个斜率不会为0 的性质,神经网络的学习得以正确进行。
4.3 数值微分
4.3.1 导数
导数就是表示某个瞬间的变化量。它可以定义成下面的式子。
下面的实现如何?# 不好的实现示例 def numerical_diff(f, x): h = 10e-50 return (f(x+h) - f(x)) / h # 好的实现示例 def numerical_diff(f, x): h = 1e-4 # 0.0001 return (f(x+h) - f(x-h)) / (2*h)这个函数有两个参数,即“函数 f ”和“传给函数 f的参数x ”。 乍一看这个实现没有问题,但是实际上这段代码有两处需要改进的地方。第一个改进的地方是:舍入误差(rounding error )。所谓舍入误差,是指因省略小数的精细部分的数值(比如,小数点第8 位以后的数值)而造成最终的计算结果上的误差。比如,在Python 中,舍入误差可如下表示。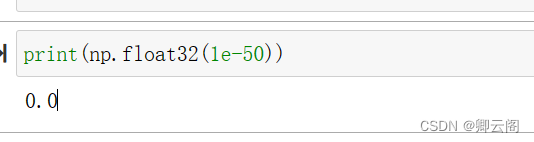 如上所示,如果用 float32 类型( 32 位的浮点数)来表示 1e-50 ,就会变成 0. 0 ,无法正确表示出来。也就是说,使用过小的值会造成计算机出现计算上的问题。这是第一个需要改进的地方,即将微小值h 改为
如上所示,如果用 float32 类型( 32 位的浮点数)来表示 1e-50 ,就会变成 0. 0 ,无法正确表示出来。也就是说,使用过小的值会造成计算机出现计算上的问题。这是第一个需要改进的地方,即将微小值h 改为。使用
就可以得到正确的结果。
第二个需要改进的地方与函数f 的差分有关。虽然上述实现中计算了函数f 在 x+h 和 x 之间的差分,但是必须注意到,这个计算从一开始就有误差。 “真的导数”对应函数在 x 处的斜率(称为切线),但上述实现中计算的导数对应的是( x + h ) 和 x 之间的斜率。因此,真的导数(真的切线)和上述实现中得到的导数的值在严格意义上并不一致。这个差异的出现是因为h 不可能无限接近 0 。
4.3.2 数值微分的例子
现在我们试着用上述的数值微分对简单函数进行求导。先来看一个由下式表示的2 次函数。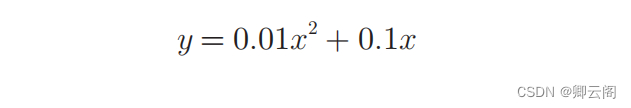
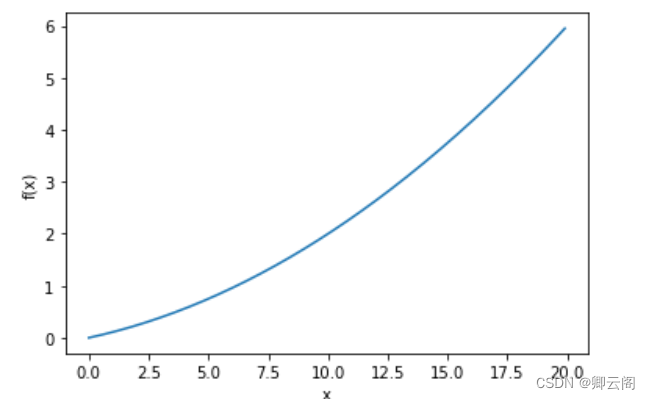
def function_1(x): return 0.01*x**2 + 0.1*x接下来,我们来绘制这个函数的图像。画图所用的代码如下。
我们来计算一下这个函数在x = 5和x = 10处的导数。
#计算导数 print("-----x = 5处的导数-----") print("x = 5处的导数={0}".format( numerical_diff(function_1, 5))) print("-----x = 10处的导数-----") print("x = 10处的导数={0}".format( numerical_diff(function_1, 10))) 这里计算的导数是 f ( x ) 相对于 x 的变化量,对应函数的斜率。另外, f ( x ) = 0 . 01 x 2 + 0 . 1 x 的解析解是。因 此,在 x = 5 和 x = 10 处,“真的导数”分别为 0 . 2 和 0 . 3。和上面的结果相比,我们发现虽然 严格意义上它们并不一致,但误差非常小。实际上,误差小到基本上可以认为它们是相等的。x = 5 、 x = 10 处的切线:直线的斜率使用数值微分的值
这里计算的导数是 f ( x ) 相对于 x 的变化量,对应函数的斜率。另外, f ( x ) = 0 . 01 x 2 + 0 . 1 x 的解析解是。因 此,在 x = 5 和 x = 10 处,“真的导数”分别为 0 . 2 和 0 . 3。和上面的结果相比,我们发现虽然 严格意义上它们并不一致,但误差非常小。实际上,误差小到基本上可以认为它们是相等的。x = 5 、 x = 10 处的切线:直线的斜率使用数值微分的值4.3.3 偏导数
这里有两个变量。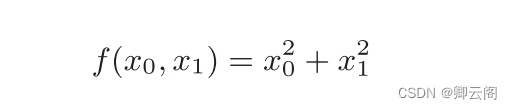
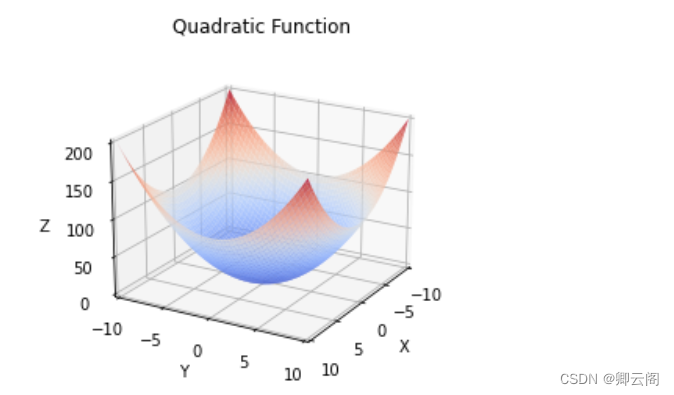
这个式子可以用Python来实现,如下所示。这里,我们假定向参数输入了一个NumPy数组。函数的内部实现比较 简单,先计算NumPy数组中各个元素的平方,再求它们的和(np.sum(x**2) 也可以实现同样的处理)。我们来画一下这个函数的图像。结果如图4-8所示, 是一个三维图像。
现在我们导数。这里需要注意的是,有两个变量, 所以有必要区分对哪个变量求导数,即对x 0 和 x 1 两个变量中的哪一个求导数。 另外,我们把这里讨论的有多个变量的函数的导数称为偏导数。
怎么求偏导数呢?我们先试着解一下下面两个关于偏导数的问题。问题1 :求 x 0 = 3 , x 1 = 4 时,关于 x 0 的偏导数问题2 :求 x 0 = 3 , x 1 = 4时,关于 x 1 的偏导数
4.4 梯度
现在,我们用这个函数实际计算一下梯度。这里我们求点(3 , 4) 、 (0 , 2) 、 (3 , 0) 处的梯度。def numerical_gradient(f, x): h = 1e-4 # 0.0001 grad = np.zeros_like(x) # 生成和x形状相同的数组 for idx in range(x.size): tmp_val = x[idx] # f(x+h)的计算 x[idx] = tmp_val + h fxh1 = f(x) # f(x-h)的计算 x[idx] = tmp_val - h fxh2 = f(x) grad[idx] = (fxh1 - fxh2) / (2*h) x[idx] = tmp_val # 还原值 return grad #计算导数 print("-----点(3, 4)处的梯度-----") print("点(3, 4)处的梯度={0}".format( numerical_gradient(function_2, np.array([3.0, 4.0])))) print("-----点(0, 2)处的梯度-----") print("点(0, 2)处的梯度={0}".format( numerical_gradient(function_2, np.array([0.0, 2.0])))) print("-----点(3, 0)处的梯度-----") print("点(3, 0)处的梯度={0}".format( numerical_gradient(function_2, np.array([3.0, 0.0]))))
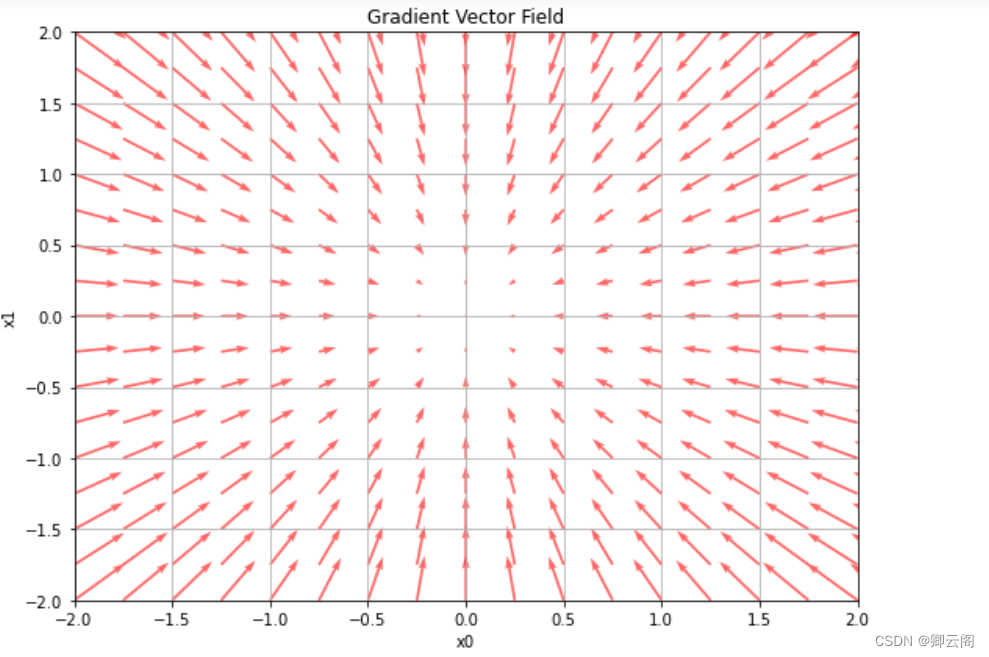
这个梯度意味着什么呢?为了更好地理解,我们把 的梯度画在图上。不过,这里我们画的是元素值为负梯度B 的向量。import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D def _numerical_gradient_no_batch(f, x): h = 1e-4 grad = np.zeros_like(x) for idx in range(x.size): tmp_val = x[idx] x[idx] = float(tmp_val) + h fxh1 = f(x) x[idx] = tmp_val - h fxh2 = f(x) grad[idx] = (fxh1 - fxh2) / (2 * h) x[idx] = tmp_val return grad def numerical_gradient(f, X): if X.ndim == 1: return _numerical_gradient_no_batch(f, X) else: grad = np.zeros_like(X) for idx, x in enumerate(X): grad[idx] = _numerical_gradient_no_batch(f, x) return grad def function_2(x): if x.ndim == 1: return np.sum(x ** 2) else: return np.sum(x ** 2, axis=1) def tangent_line(f, x): d = numerical_gradient(f, x) y = f(x) - d * x return lambda t: d * t + y if __name__ == '__main__': x0 = np.arange(-2, 2.5, 0.25) x1 = np.arange(-2, 2.5, 0.25) X, Y = np.meshgrid(x0, x1) X = X.flatten() Y = Y.flatten() grad = numerical_gradient(function_2, np.array([X, Y])) plt.figure(figsize=(8, 6)) plt.quiver(X, Y, -grad[0], -grad[1], angles="xy", color="red", alpha=0.6, scale=70) plt.xlim([-2, 2]) plt.ylim([-2, 2]) plt.xlabel('x0') plt.ylabel('x1') plt.title('Gradient Vector Field') plt.grid(True) plt.tight_layout() plt.show()
梯度呈现为有向向量(箭头)。观察图 ,我们发现梯度指向函数 f ( x 0 ,x 1 ) 的“最低处”(最小值),就像指南针 一样,所有的箭头都指向同一点。其次,我们发现离“最低处”越远,箭头越大。虽然图 4-9 中的梯度指向了最低处,但并非任何时候都这样。实际上, 梯度会指向各点处的函数值降低的方向。更严格地讲,梯度指示的方向是各点处的函数值减小最多的方向。4.4.1 梯度法
通过巧妙地使用梯度来寻找函数最小值 (或者尽可能小的值)的方法就是梯度法。梯度表示的是各点处的函数值减小最多的方向。因此, 无法保证梯度所指的方向就是函数的最小值或者真正应该前进的方向。实际上,在复杂的函数中,梯度指示的方向基本上都不是函数值最小处。我们尝试用数学式来表示梯度法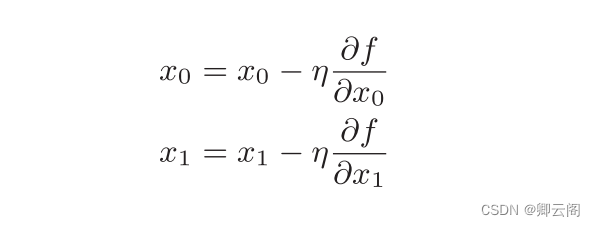 η 表示更新量,在神经网络的学习中,称为 学习率 ( learning rate)。学习率决定在一次学习中,应该学习多少,以及在多大程度上更新参数。学习率需要事先确定为某个值,比如 0 . 01 或 0 . 001 。一般而言,这个值过大或过小,都无法抵达一个“好的位置”。在神经网络的学习中,一般会一边改变学习率的值,一边确认学习是否正确进行了。 下面,我们用Python 来实现梯度下降法。如下所示,这个实现很简单。
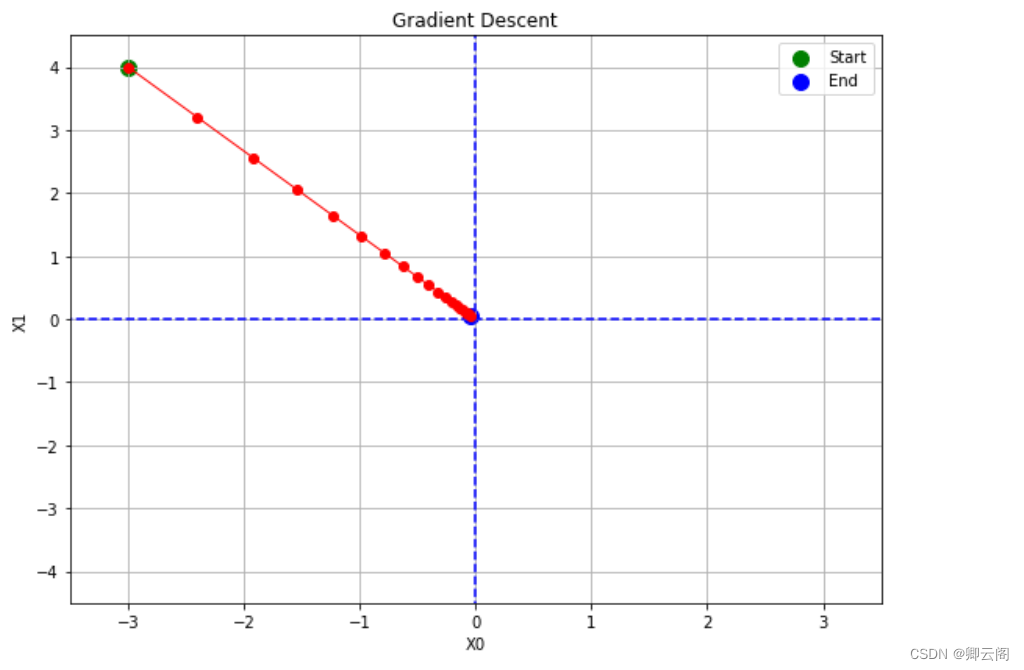
η 表示更新量,在神经网络的学习中,称为 学习率 ( learning rate)。学习率决定在一次学习中,应该学习多少,以及在多大程度上更新参数。学习率需要事先确定为某个值,比如 0 . 01 或 0 . 001 。一般而言,这个值过大或过小,都无法抵达一个“好的位置”。在神经网络的学习中,一般会一边改变学习率的值,一边确认学习是否正确进行了。 下面,我们用Python 来实现梯度下降法。如下所示,这个实现很简单。def gradient_descent(f, init_x, lr=0.01, step_num=100): x = init_x for i in range(step_num): grad = numerical_gradient(f, x) x -= lr * grad return x参数 f 是要进行最优化的函数, init_x 是初始值, lr 是学习率 learning rate, step_num 是梯度法的重复次数。 numerical_gradient(f,x) 会求函数的梯度,用该梯度乘以学习率得到的值进行更新操作,由step_num 指定重复的次数。 使用这个函数可以求函数的极小值,顺利的话,还可以求函数的最小值。 下面,我们就来尝试解决下面这个问题。问题:请用梯度法求最小值。 这里,设初始值为 (-3.0, 4.0) ,开始使用梯度法寻找最小值。最终的结 果是(-6.1e-10, 8.1e-10) ,非常接近 (0 , 0) 。实际上,真的最小值就是 (0 , 0) , 所以说通过梯度法我们基本得到了正确结果。如果用图来表示梯度法的更新 过程。
这里,设初始值为 (-3.0, 4.0) ,开始使用梯度法寻找最小值。最终的结 果是(-6.1e-10, 8.1e-10) ,非常接近 (0 , 0) 。实际上,真的最小值就是 (0 , 0) , 所以说通过梯度法我们基本得到了正确结果。如果用图来表示梯度法的更新 过程。
前面说过,学习率过大或者过小都无法得到好的结果。我们来做个实验验证一下。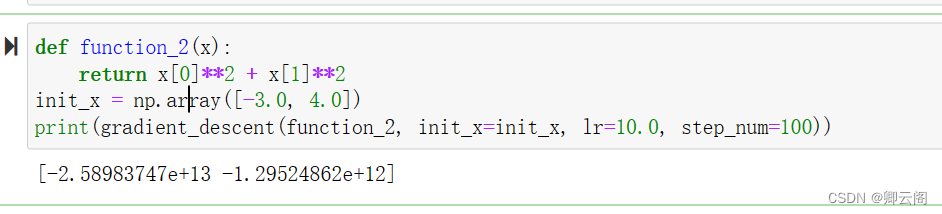
实验结果表明,学习率过大的话,会发散成一个很大的值;反过来,学习率过小的话,基本上没怎么更新就结束了。也就是说,设定合适的学习率是一个很重要的问题。4.4.2 神经网络的梯度
神经网络的学习也要求梯度。这里所说的梯度是指损失函数关于权重参数的梯度。比如,有一个只有一个形状为2 × 3 的权重 W 的神经网络。 下面,我们以一个简单的神经网络为例,来实现求梯度的代码。为此, 我们要实现一个名为simpleNet 的类。
下面,我们以一个简单的神经网络为例,来实现求梯度的代码。为此, 我们要实现一个名为simpleNet 的类。# coding: utf-8 import sys, os sys.path.append(os.pardir) # 为了导入父目录中的文件而进行的设定 import numpy as np from common.functions import softmax, cross_entropy_error from common.gradient import numerical_gradient class simpleNet: def __init__(self): self.W = np.random.randn(2,3) def predict(self, x): return np.dot(x, self.W) def loss(self, x, t): z = self.predict(x) y = softmax(z) loss = cross_entropy_error(y, t) return loss x = np.array([0.6, 0.9]) t = np.array([0, 0, 1]) net = simpleNet() f = lambda w: net.loss(x, t) dW = numerical_gradient(f, net.W) print(dW)simpleNet 类只有 一个实例变量,即形状为2 × 3 的权重参数。它有两个方法,一个是用于预 测的predict(x) ,另一个是用于求损失函数值的 loss(x,t) 。这里参数 x 接收输入数据,t 接收正确解标签。现在我们来试着用一下这个 simpleNet 。
4.5 学习算法的实现
前提神经网络存在合适的权重和偏置,调整权重和偏置以便拟合训练数据的过程称为“学习”。神经网络的学习分成下面 4 个步骤。步骤1(mini-batch)从训练数据中随机选出一部分数据,这部分数据称为 mini-batch 。我们的目标是减小 mini-batch 的损失函数的值。步骤2(计算梯度)为了减小 mini-batch 的损失函数的值,需要求出各个权重参数的梯度。梯度表示损失函数的值减小最多的方向。步骤3(更新参数)将权重参数沿梯度方向进行微小更新。步骤4(重复)重复步骤 1 、步骤 2 、步骤 3 。神经网络的学习按照上面 4 个步骤进行。这个方法通过梯度下降法更新参数,不过因为这里使用的数据是随机选择的mini batch 数据,所以又称为随机梯度下降法( stochastic gradient descent )。“随机”指的是“随机选择的” 的意思,因此,随机梯度下降法是“对随机选择的数据进行的梯度下降法”。 深度学习的很多框架中,随机梯度下降法一般由一个名为SGD 的函数来实现。 SGD来源于随机梯度下降法的英文名称的首字母。
0基础入门---第四章---神经网络的学习
news2026/2/14 7:23:34
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/691621.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
【突发小技巧】手动将jar包导入本地Maven仓库
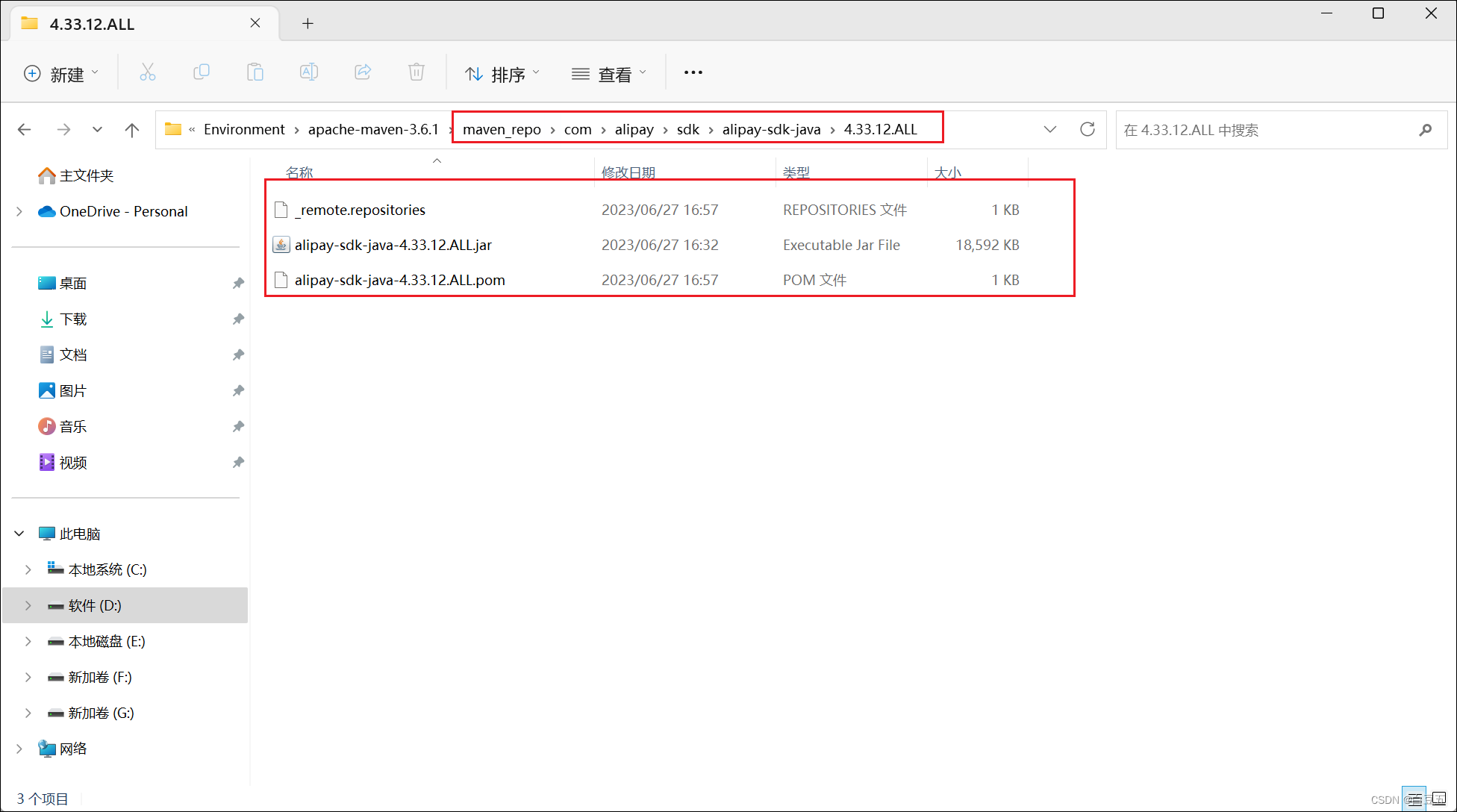
1、下载jar包 以支付宝sdk为例:https://mvnrepository.com/artifact/com.alipay.sdk/alipay-sdk-java/4.33.12.ALL 后面执行mvn install命令(也就是安装命令,生命周期:编译、测试、打包、安装),也会参考这个依赖坐标: …
前端安全 - 保护你的应用免受攻击的关键
80. 前端安全 - 保护你的应用免受攻击的关键
作为前端工程师,我们不仅需要关注用户界面的设计和功能实现,还需要关注应用程序的安全性。前端安全是保护我们的应用程序免受恶意攻击和数据泄露的重要方面。本文将介绍前端安全的概念、常见的安全威胁以及一…
Linux集群服务器上运行命令的4个实用工具
目录
1. PSSH-Parallel SSH 安装parallel-ssh,
使用
2. Pdsh-并行远程Shell实用程序
3. ClusterSSH
安装
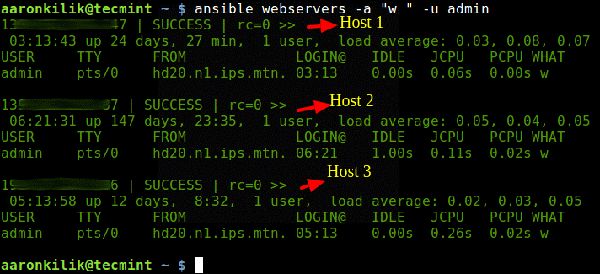
4. Ansible 我们假设你已经设置好了SSH以便访问所有服务器;其次假设,同时访问多台服务器时,在所有Linux服务器上设置基于密钥的无…
Vue+vite创建项目关于vite.config.js文件的配置
Vuevite创建项目关于vite.config.js文件的配置
Vue项目创建时,我们见过vue-cli 创建项目和webpack 创建项目等方式。 现在Vue 3版本使用npm/pnpm create vuelatest 创建项目,是搭配使用vite工具构建的。 创建完成的项目,最明显的去别就是&am…
【硬件自动化软件设计及实现】如何设计并实现!
今天来聊聊关于硬件方向的自动化软件设计及实现,后面我会用实例来让我们更加深入的了解硬件自动化,首先开发工具选择的是python语言,为啥选择python语言呢,因为他的语法比较简洁,外置库非常多,反正就是对于做自动化方面很实用就对了。 1.硬件自动化测试大致分为三个阶段实…
Redis 来了,Navicat 用户炸开了锅 | 文末附免单王获奖名单
近期,Navicat 的后台热闹无比!自 2023 年 5 月 Navicat Premium 16.2 Beta 中文版上线以来,童鞋们的留言如潮水般涌来。6 月中旬,我们正式发布了 Navicat Premium 16.2 与 Navicat for Redis,赋予了Navicat 更卓越的功…
JMeter工具接口性能压力测试分析与优化
目录 前言:
一、具体测试结果如下:
二、初始应用配置调整:
三、分析解决过程:
总结: 前言:
最近公司做的项目,要求对相关接口做性能压力测试,在这里记录一下分析解决过程。
压…
[Pytorch]导数与求导
文章目录 导数与求导一. 标量 向量 矩阵 的导数二.Pytorch中的反向求导.backward()三.非标量求导 导数与求导
一. 标量 向量 矩阵 的导数
标量,向量,矩阵间求导后的形状:
y\x标量x(1)向量 x(n,1)矩阵 X(n,k)标量y(1)(1)(1,n)(k,n)向量 y(m…
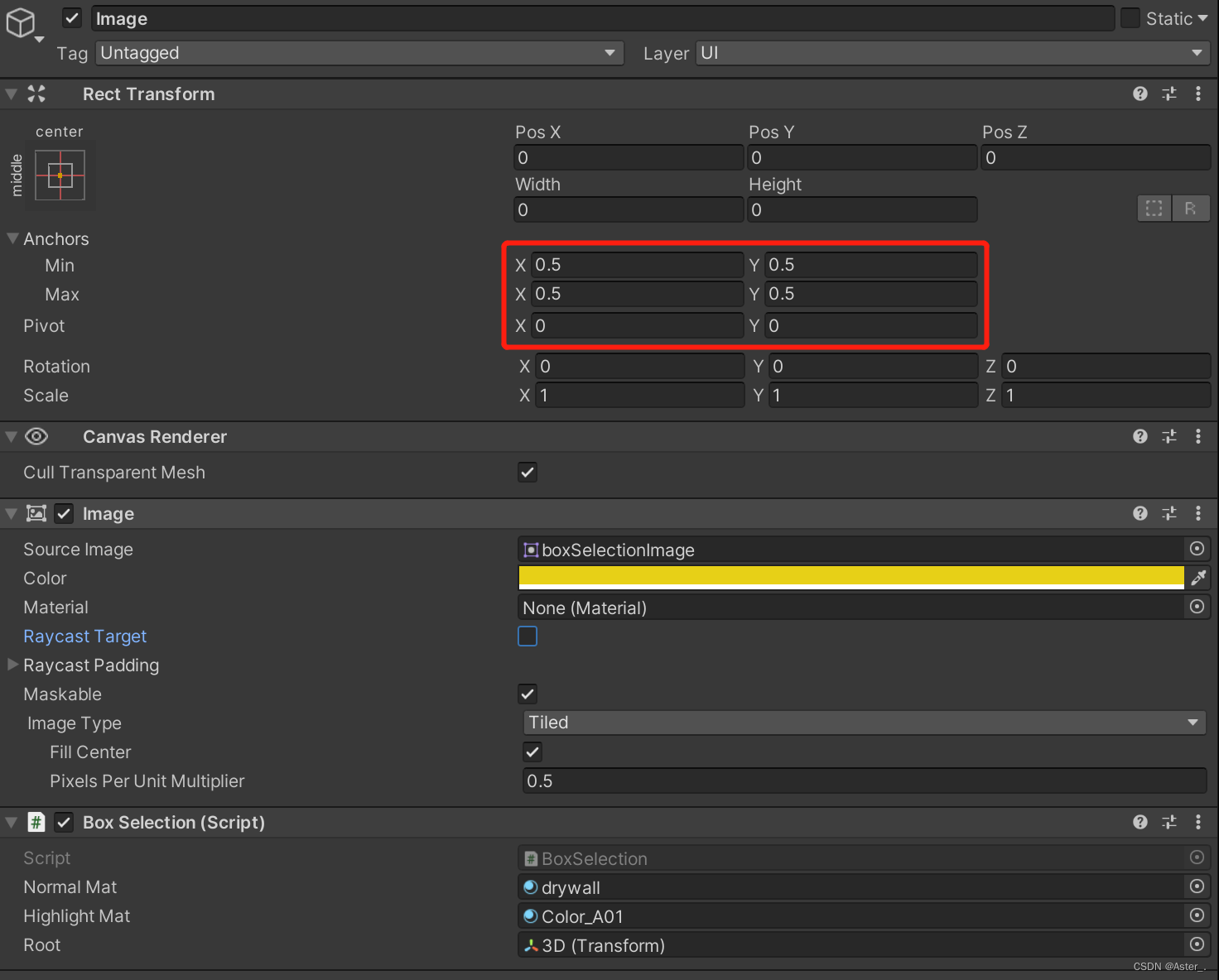
Unity Image/GL实现一个框选功能吧
场景准备 准备一张框选背景图 导入到unity之后,修改 Texture Type 为 Sprite,(根据图片需要)在 Sprite Editor 中 编辑 九宫格格式。图片样式的不一致,设置的九宫格格式也不一致。本例中虚线部分需要等距离平铺&…
Visual C++类的继承及类中成员的访问特性——搞懂public、protected、private
我是荔园微风,作为一名在IT界整整25年的老兵,今天来说说Visual C中类的继承及类中成员的访问特性,也就是来搞懂public、protected、private这三个东西。
很多人搞不清楚这三个东西,并且很容易弄错,其实不是学习的人的…
vr全景在线虚拟展馆节约企业成本费用
博物馆作为人们了解历史、文化和艺术的重要场所,现在可以通过VR全景技术来进行展览,让参观者身临其境地感受历史文化的魅力。本文将介绍博物馆VR全景的特点、优势,以及如何使用VR全景技术来使得博物馆的展览和教育活动更丰富。 参观者可以对内…
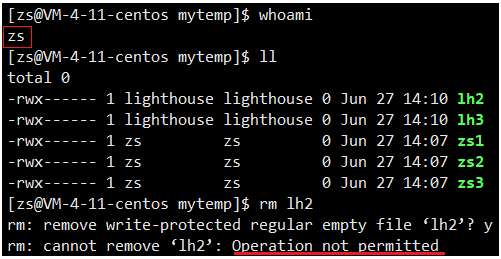
【Linux】权限理解
Linux权限理解 shell外壳运行原理为什么我们不是直接访问操作系统?外壳程序的意义 权限的概念与操作用户的权限如何进行Linux下用户身份的切换? 角色和文件的权限权限是什么?Linux中文件的类型是如何被确定的?权限与角色的关系权限与文件属性…
玩机搞机---修改系统固件不开机 安卓13去除系统app签名验证的几种方法
谷歌在安卓13中对系统应用添加了一层校验验证,你如果修改了系统app.那么原有的签名加载后过不去验证,会导致进不去系统卡第一屏或者进入系统后修改的app错误等等故障。
Android 13增加了新的apk签名校验机制,现在开机中它会对所有系统分区&a…
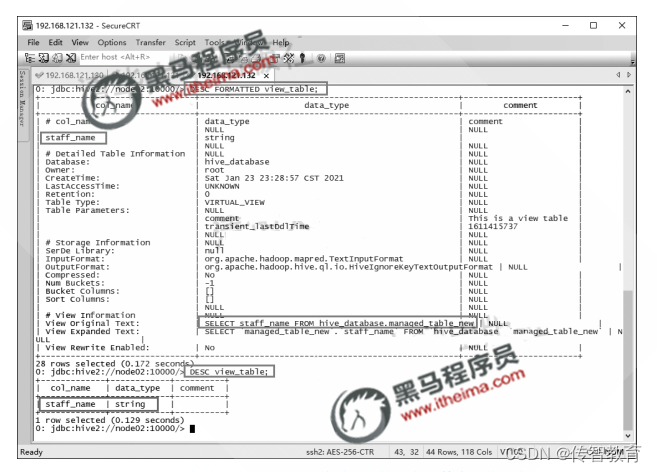
Hive中怎样创建和查询视图信息?
视图是从数据库的数据表中选取出来的数据组成的逻辑窗口,它是一个虚拟机表。引入视图后,用户可以将注意力集中在关心的数据上,如果数据来源于多个基本表结构,并且搜索条件比较复杂时,需要编写的查询语句就会比较烦琐&a…
hivesql 将数据处理成复杂json
类型一
原数据:bankid是array类型 目标数据:
{"bankname": ["SPDB", "WS_HBBANK", "mytest"],"grid": [{"name": "阶段1","values": ["38.0,1.0,1.0"]}…
安全生产月评选活动-优秀的“安全之星”,塑造榜样力量
安全生产月评选活动-优秀的“安全之星”,塑造榜样力量。
推荐功能:投票 企业可以举办安全生产月评选活动,选出优秀的“安全之星”,进行内部评选,塑造榜样力量。 首先,让我们先来了解一下“安全生产月评选活…
MYSQL各种log
本章纲要
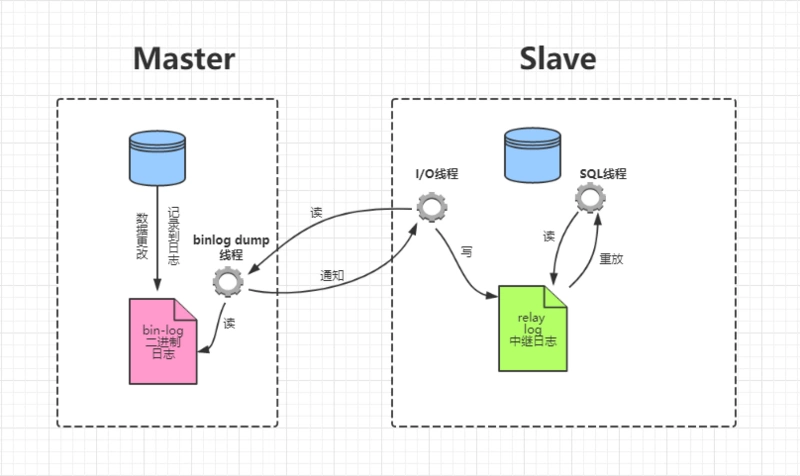
1、mysql主从复制是怎么实现的(binlog,relaylog)
2、事物执行原理是怎么保证ACID的(redolog,undolog)
一、Mysql是怎么实现主从复制的 数据库主从设计的好处:
1、实现读写分离,方便扩展&#…
MySQL 磁盘爆了,是 optimize table 的锅
2023-06-26 22:17左右,收到某系统的主库磁盘使用率告警。2023-06-26 23:02左右收到该系统的从库磁盘使用率告警。 收到告警后,登录数据库查看各表的磁盘使用。 经分析发现DB存在一个当日的备份表t_eap_sys_navigation_log_bak_20230626 ,且在…
4077:出栈序列统计
codeup【递归入门】出栈序列统计_codeup编程_战斗的咸鱼的博客-CSDN博客 #include<iostream>
using namespace std;
int n,sum,ans;
void dfs(int out,int in,int not_in){if(outn){ans;return;}if(in>0) dfs(out1,in-1,not_in);if(not_in>0&&in<n) dfs…


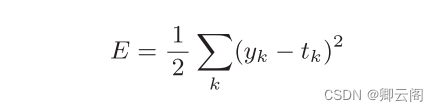
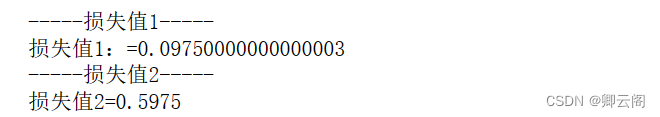


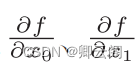






![[Pytorch]导数与求导](https://img-blog.csdnimg.cn/3d4162d08a624b87a14239b65c1ff381.jpeg)