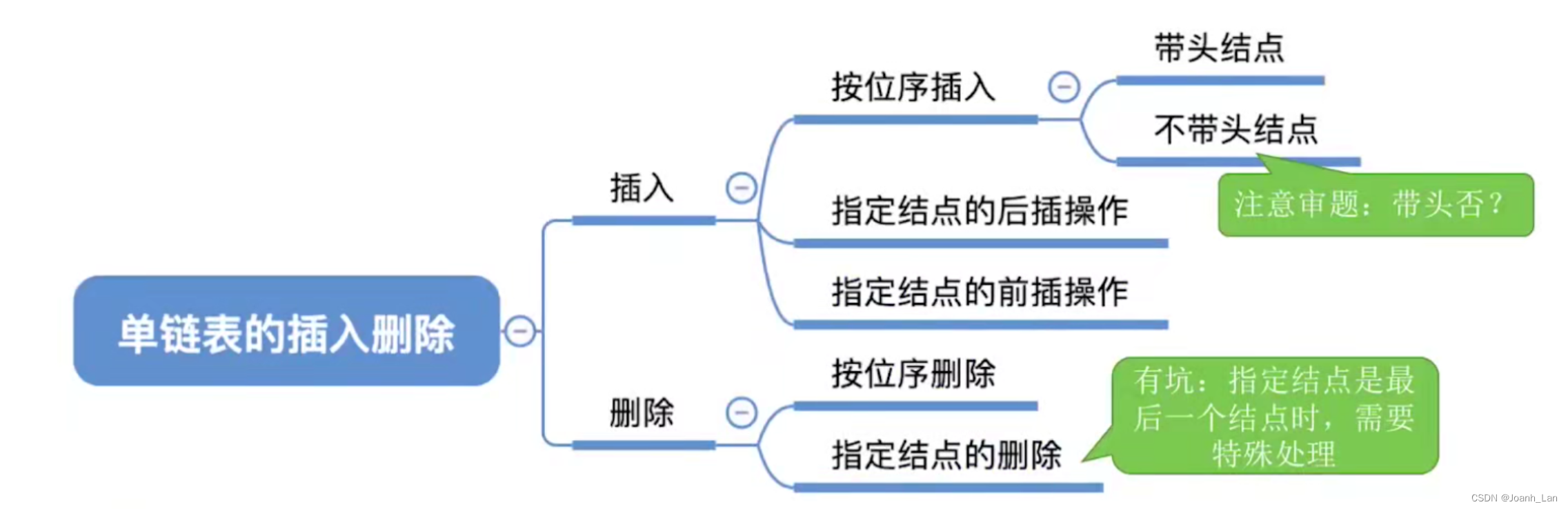
数据结构–单链表的插入&删除
目标
单链表的插入(位插、前插、后插)
单链表的删除
单链表的插入
按为序插入(带头结点)
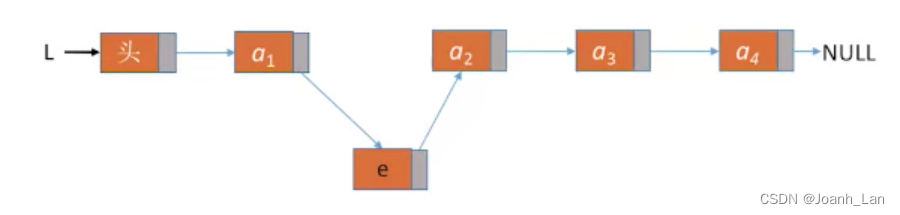
ListInsert(&L,i,e):插入操作。在表L中的第i个位置上插入指定元素e。
思路:找到第i-1个结点,将新结点插入其后
代码实现
typedef struct LNode
{
ElemType data;
struct LNode *next;
}LNode, *LinkList;
bool ListInsert(LinkList &L, int i, ElemType e)
{
if (i < 1) return false;
LNode *p = L; //L指向头结点,头结点是第0个结点(不存数据)
int j = 0; //当前p指向的是第几个结点
while (p != NULL && j < i - 1) //循环找到第i-1个结点
{
p = p->next;
j++;
}
if (p == NULL) return false;
LNode* s = (LNode*)malloc(sizeof(LNode));
s->next = p->next;
s->data = e;
p->next = s;
return true;
}
时间复杂度
最好时间复杂度 O(1)
最坏时间复杂度 O(1)
平均时间复杂度 O(1)
按位序插入(不带头结点)
思路:找到第i-1个结点,将新结点插入其后

代码实现
typedef struct LNode
{
ElemType data;
struct LNode *next;
}LNode, *LinkList;
bool ListInsert(LinkList &L, int i, ElemType e)
{
if (i < 1) return false;
if (i == 1) //插入第1个结点的操作与其他结点操作不同
{
LNode* s = (LNode*)malloc(sizeof(LNode));
s->data = e;
s->next = L;
L = s;
return true;
}
LNode *p = L; //L指向头结点,头结点是第0个结点(不存数据)
int j = 0; //当前p指向的是第几个结点
while (p != NULL && j < i - 1) //循环找到第i-1个结点
{
p = p->next;
j++;
}
if (p == NULL) return false;
LNode* s = (LNode*)malloc(sizeof(LNode));
s->next = p->next;
s->data = e;
p->next = s;
return true;
}
结论:
不带头写代码更不方便,推荐用带头结点
注意:考试中带头、不带头都有可能考察,注意审题
指定结点的后插操作
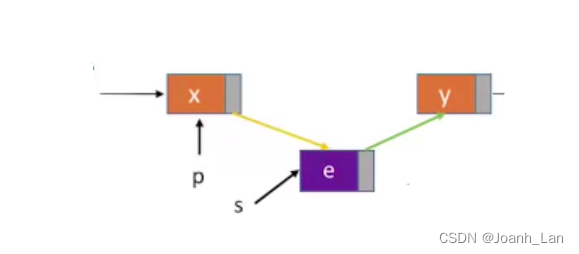
代码实现
typedef struct LNode
{
ElemType data;
struct LNode *next;
}LNode, *LinkList;
bool InsertNextNode(LNode* p, ElemType e)
{
if (p == NULL) return false;
LNode* s = (LNode*)malloc(sizeof(LNode));
if (s == NULL) return false; // 内存分配失败
s->data = e;
s->next = p->next;
p->next = s;
return true;
}
指定结点的前插操作
前插操作:在p结点之前插入元素e
bool InsertPriorNode (LNode *p,ElemType e)

方法一:
bool InsertPriorNode (LinkListL L, Node *p,ElemType e)
传入头指针,循环查找p的前驱,再对q后插
时间复杂度:O(n)
方法二 \color{red}方法二 方法二
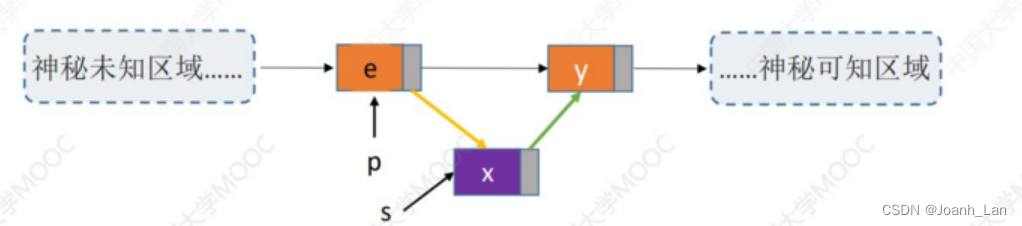
方法二实现代码
typedef struct LNode
{
ElemType data;
struct LNode *next;
}LNode, *LinkList;
bool InsertPriorNode (LNode *p,ElemType e)
{
if (p == NULL) return false;
LNode* s = (LNode*)malloc(sizeof(LNode));
if (s == NULL) return false;
s->next = p->next;
p->next = s; //新结点s连到p之后
s->data = p->data; //将p中元素复制到s中
p->data = e; //p 中元素覆盖为e
return true;
}
时间复杂度: O(n)
前插操作:在p结点之前插入结点 s
代码实现
bool InsertPriorNode(LNode* p, LNode* s)
{
if (p == NULL || s == NULL) return false;
s->next = p->next;
p->next = s;
ElemType tmp = p->data;
p->data = s->data;
s->data = tmp;
return true;
}
单链表的删除
按位序删除(带头结点)
ListDelete(&L,i,&e):删除操作。删除表L中第i个位置的元素,并用e返回删除元素的值。
方法:
找到第i-1个结点,将其指针指向第i+1个结点,并释放第i个结点
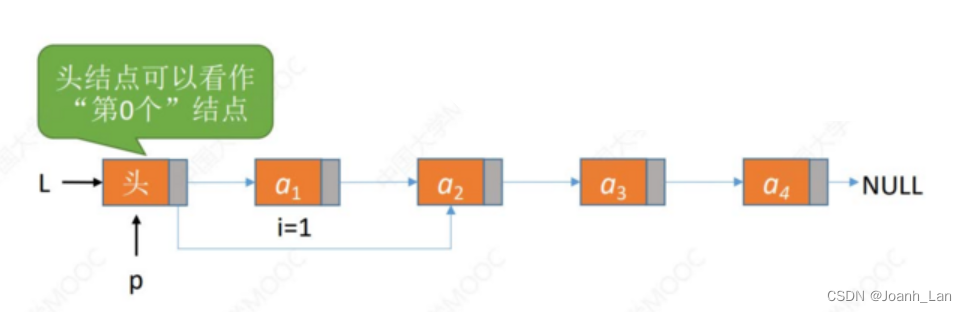
代码实现
typedef struct LNode
{
ElemType data;
struct LNode *next;
}LNode, *LinkList;
bool ListDelete(LinkList &L, int i, ElemType &e)
{
if (i < 1) return false;
LNode *p = L;
int j = 0;
while (p != NULL && j < i - 1)
{
p = p->next;
j++;
}
if (p == NULL) return false;
if (p->next == NULL) return false; //第i-1个结点之后已无其他结点
LNode* q = p->next;
e = q->data; //用e返回元素的值
p->next = q->next; //将*q结点从链中“断开"
free(q); //释放结点的存储空间
return true;
}
时间复杂度:O(n)
删除指定结点p
bool DeleteNode ( LNode *p)
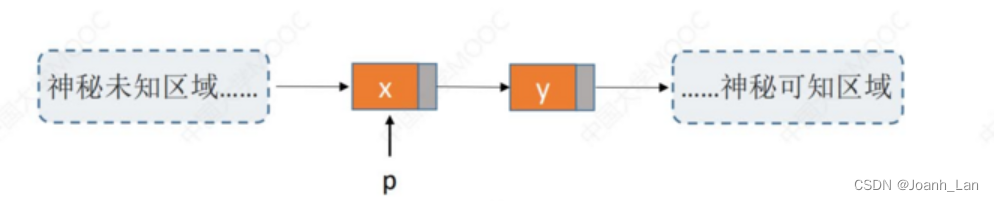
方法1:传入头指针,循环寻找p的前驱结点
时间复杂度O(n)
方法2:偷天换日(类似于结点前插的实现)
时间复杂度O(1)
方法二代码实现
typedef struct LNode
{
ElemType data;
struct LNode *next;
}LNode, *LinkList;
bool DeleteNode(LNode* p)
{
if (p == NULL) return false;
LNode* q = p->next; //令q指向*p的后继结点
p->data = p->next->data; //和后继结点交换数据域
p->next = q->next; //将*q结点从链中"断开"
free(q);
return true;
}
注:
\color{red}注:
注:
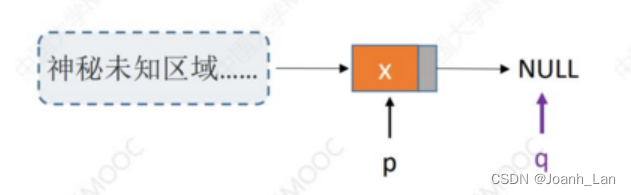
如果
p
是最后一个结点,只能从表头开始依次寻找
p
的前驱
,
时间复杂度
O
(
n
)
\color{red} 如果p是最后一个结点,只能从表头开始依次寻找p的前驱,时间复杂度O(n)
如果p是最后一个结点,只能从表头开始依次寻找p的前驱,时间复杂度O(n)
知识点回顾与重要考点