Maximum White Subtree - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题意：

思路：

先去树形DP求出DP值，这很好求

设dp[u]为以u为根的子树中白-黑的最大值

初始化就是：如果u本身是黑，那dp[u]=-1，否则dp[u]=1

void dfs1(int u,int fa){
    if(a[u]==0) dp[u]=-1;//黑点
    else dp[u]=1;//白点
    for(int i=head[u];~i;i=edge[i].next){
        if(edge[i].to==fa) continue;
        dfs1(edge[i].to,u);
        if(dp[edge[i].to]>0) dp[u]+=dp[edge[i].to];
    }
}

然后考虑换根

这里我想烦了，我想的是把S2求出来，看S2是否>0，如果是就加上，否则就不加：

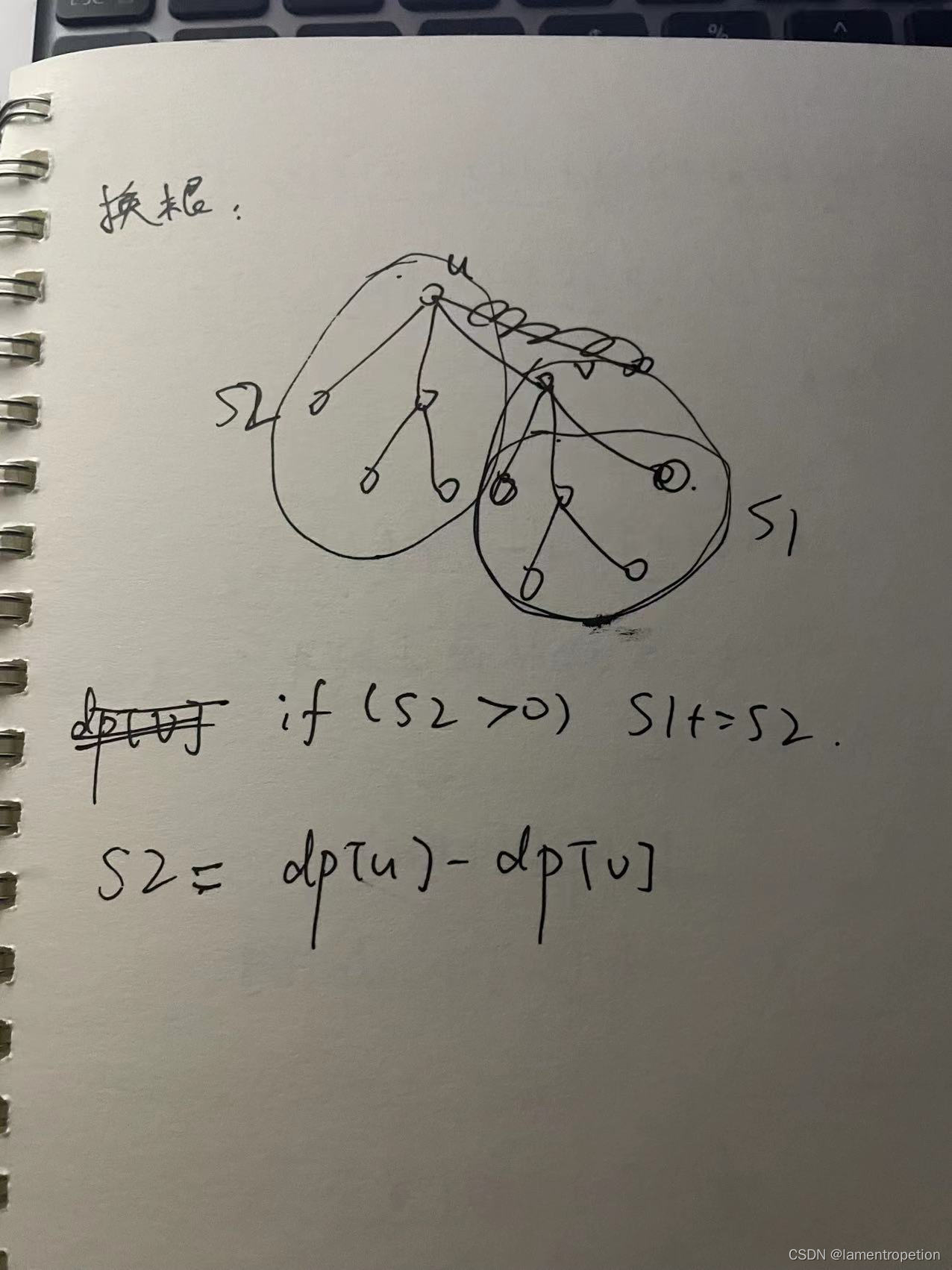
事实上，S2很难求，根本不需要去求它

我们只需要知道加上u的除了v部分的子树之后，和原来相比，哪个大就行

因此只需要把dp[v]分类讨论即可

void dfs2(int u,int fa){
    for(int i=head[u];~i;i=edge[i].next){
        if(edge[i].to==fa) continue;
        if(dp[edge[i].to]>0){
            dp[edge[i].to]=max(dp[edge[i].to],dp[u]);
        }else{
            dp[edge[i].to]=max(dp[edge[i].to],dp[u]+dp[edge[i].to]);
        }
        dfs2(edge[i].to,u);
    }
}

 

Code：

#include <bits/stdc++.h>

#define int long long

using namespace std;

using i64 = long long;

const int mxn=1e6+10;
const int mxe=1e6+10;
const int mod=1e9+7;

struct ty{
    int to,next;
}edge[mxe<<2];

int N,u,v;
int tot=0;
int a[mxn];
int head[mxn];
int dp[mxn];

void add(int u,int v){
    edge[tot].to=v;
    edge[tot].next=head[u];
    head[u]=tot++;
}
void G_init(){
    tot=0;
    for(int i=0;i<=N;i++){
        head[i]=-1;
    }
}
void dfs1(int u,int fa){
    if(a[u]==0) dp[u]=-1;//黑点
    else dp[u]=1;//白点
    for(int i=head[u];~i;i=edge[i].next){
        if(edge[i].to==fa) continue;
        dfs1(edge[i].to,u);
        if(dp[edge[i].to]>0) dp[u]+=dp[edge[i].to];
    }
}
void dfs2(int u,int fa){
    for(int i=head[u];~i;i=edge[i].next){
        if(edge[i].to==fa) continue;
        if(dp[edge[i].to]>0){
            dp[edge[i].to]=max(dp[edge[i].to],dp[u]);
        }else{
            dp[edge[i].to]=max(dp[edge[i].to],dp[u]+dp[edge[i].to]);
        }
        dfs2(edge[i].to,u);
    }
}
void solve(){
    cin>>N;
    G_init();
    for(int i=1;i<=N;i++) cin>>a[i];
    for(int i=1;i<=N-1;i++){
        cin>>u>>v;
        add(u,v);
        add(v,u);
    }
    dfs1(1,0);
    dfs2(1,0);
    for(int i=1;i<=N;i++) cout<<dp[i]<<" \n"[i==N];
}
signed main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int __=1;//cin>>__;
    while(__--)solve();return 0;
}