二叉树的堂兄弟节点

题目描述
在二叉树中,根节点位于深度 0 处,每个深度为 k 的节点的子节点位于深度 k+1 处。
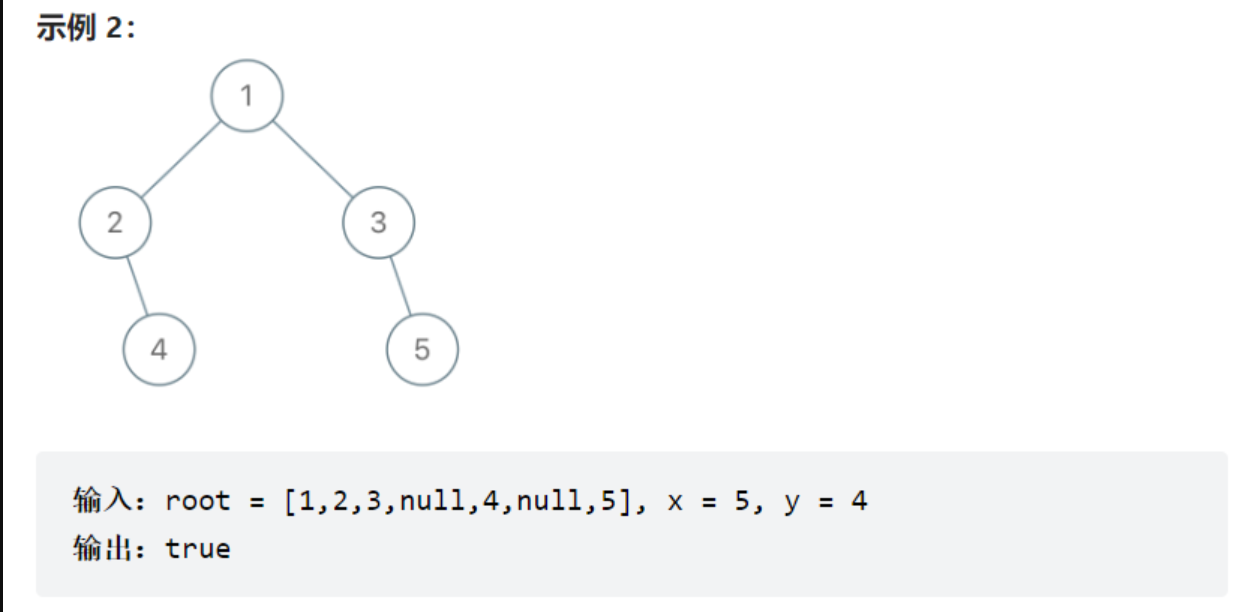
如果二叉树的两个节点深度相同,但 父节点不同 ,则它们是一对堂兄弟节点。
我们给出了具有唯一值的二叉树的根节点 root ,以及树中两个不同节点的值 x 和 y 。
只有与值 x 和 y 对应的节点是堂兄弟节点时,才返回 true 。否则,返回 false。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/cousins-in-binary-tree

提示:
二叉树的节点数介于 2 到 100 之间。
每个节点的值都是唯一的、范围为 1 到 100 的整数。
解题思路
这道题目可以通过遍历二叉树来查找节点 x 和 y,并分别记录它们的深度和父节点。如果它们深度相同但父节点不同,那么它们是堂兄弟节点,返回 true。如果二者之一未找到或深度不同,则返回 false。
具体的实现可以使用深度优先搜索或广度优先搜索来遍历二叉树。在遍历二叉树的过程中,需要记录当前节点的深度和父节点,以便在找到目标节点时方便判断是否为堂兄弟节点。
具体步骤如下:
- 定义一个存储节点深度和父节点信息的字典。
- 使用深度优先搜索或广度优先搜索遍历整个二叉树,同时记录每个节点的深度和父节点。
- 找到节点 x 和 y,分别记录它们的深度和父节点。
- 判断它们的深度是否相同,且父节点是否不同。如果满足条件,则返回 true,否则返回 false。
需要注意的是,这道题目中提到的二叉树具有唯一值的特点,因此不需要处理节点值相同的情况。
深度优先搜索
深度优先搜索(Depth First Search, DFS) 是一种基于栈或递归的搜索算法,可用于遍历或搜索树、图或其他数据结构。该算法从起点开始,不断沿着已访问但未遍历所有邻居的点向前查找,直到找到终点或达到搜素边界。当不能继续前进时,该算法回溯到最近的未访问遍历所有邻居的点,继续搜索直至找到终点。
在深度优先搜索过程中,算法递归访问每一个节点,并在访问一个节点时,将其标记为已访问。然后,算法从当前节点开始,沿着某个分支一直访问下去,只有当到达某个节点时发现它没有未访问的邻居节点时,算法才回溯到上一个节点,尝试其他的分支。
深度优先搜索算法简单易用,其实现方式既可以使用栈,也可以使用递归。它在搜索树或图中具有广泛的应用,例如可用于寻找连通块、寻找最短路径、拓扑排序、生成随机树等。其时间复杂度为 O(V+E),其中 V 表示节点数,E 表示边数。
深度优先搜索可以应用于图、树或其他数据结构的遍历和搜索问题,包括以下范围:
- 有向无环图(Directed Acyclic Graph, DAG)的拓扑排序。
- 连通性问题,例如求解连通块、最短路径、所有路径等。
- 生成随机树(Random Tree)。
- 检测环(Cycle Detection)。
- 检查图是否为二分图(Bipartite Graph)。
- 解决迷宫问题(Maze Problem)。
- 在学习和人工智能领域中,用于搜索特定模式或满足特定条件的状态空间。
除了上述范围之外,深度优先搜索还可以在其他类型的问题上发挥作用,例如,在博弈搜索问题中,可以使用深度优先搜索解决棋局状态的搜索。但是,深度优先搜索不适合解决一些特定的搜索问题,例如需要找到最优解或解决动态规划问题,因为它 不保证找到最短路径。
广度优先搜索
广度优先搜索(Breadth First Search, BFS)是一种基于队列的搜索算法,可用于遍历或搜索树、图或其他数据结构。该算法从起点开始,按照距离逐层向外探索,直到找到终点或遍历完整张图。
在广度优先搜索过程中,算法首先访问起点并将其加入队列中。然后从队列中取出下一个节点并访问其所有未访问过的相邻节点,将其加入队列中。不断重复此过程,直到找到终点或队列为空。此时,算法的搜索过程就结束了。
相比于深度优先搜索,广度优先搜索能够确保找到的路径是离起点最近的路径,但一般情况下需要更多的空间用于存储节点和边相邻节点信息。
广度优先搜索算法的时间复杂度为 O(V+E),其中 V 表示节点数,E 表示边数。算法的实现通常使用队列进行辅助,存储已经访问的节点。在实现过程中,需要额外记录每个节点到起点的距离,以便在搜索到目标节点时能够返回最短路径。广度优先搜索也可以应用于迷宫问题、最短路径问题和网络图等复杂应用中。
广度优先搜索可以应用于图、树或其他数据结构的遍历和搜索问题,包括以下范围:
- 求解最短路径问题(Shortest Path Problem)。
- 求解迷宫问题(Maze Problem)。
- 求解通信网络问题(Communication Network Problem)。
- 解决状态转移问题(State-Transition Problem),例如在人工智能领域中寻找最优解的问题。
- 实现拓扑排序(Topological Sorting)。
- 对存储结构为邻接矩阵或邻接表的图进行宽度搜索。
- 在搜索过程中,求解度数、连通性、直径和关键路径等问题。
总之,广度优先搜索可以应用于需要查找节点距离的问题,或者需要在图或树中搜索离起点最近的节点的问题。 与深度优先搜索不同,广度优先搜索通常更适用于搜索最短路径和计算节点之间的最短距离等问题。
题目解法
可以通过深度优先搜索和广度优先搜索两种方式来解决该问题。
首先,我们通过深度优先搜索找到x和y的父节点以及深度信息。然后,比较x和y的深度是否相同且它们的父节点是否不同,如果是,则它们是一对堂兄弟节点。
以下是使用深度优先搜索的Python代码:
class Solution:
def isCousins(self, root, x, y):
def dfs(node, parent, depth, val):
if not node:
return
if node.val == val:
return parent, depth
return dfs(node.left, node, depth+1, val) or dfs(node.right, node, depth+1, val)
x_info = dfs(root, None, 0, x)
y_info = dfs(root, None, 0, y)
return x_info[0] != y_info[0] and x_info[1] == y_info[1]
另一种方式是使用广度优先搜索,通过层序遍历二叉树找到x和y的深度和父节点。最后,比较x和y的深度是否相同且它们的父节点是否不同,如果是,则它们是一对堂兄弟节点。
以下是使用广度优先搜索的Python代码:
class Solution:
def isCousins(self, root, x, y):
queue = [(root, None)]
x_info = None
y_info = None
depth = 0
while queue:
depth += 1
for i in range(len(queue)):
node, parent = queue.pop(0)
if node.val == x:
x_info = (parent, depth)
if node.val == y:
y_info = (parent, depth)
if node.left:
queue.append((node.left, node))
if node.right:
queue.append((node.right, node))
if x_info and y_info:
break
return x_info[0] != y_info[0] and x_info[1] == y_info[1]

深度优先搜索算法优化
对于上述算法,也可以进行一些细节上的优化。比如,在递归时,可以首先判断左子树是否存在x或y,如果存在就不需要递归右子树了;反之,如果右子树存在x或y,也不需要递归左子树了。这样可以减少一些递归次数。
另外,可以使用Python中的tuple解包来获取x和y的信息,而不是使用下标来访问。
以下是进一步优化后的代码:
class Solution:
def isCousins(self, root, x, y):
def dfs(node, parent, depth, val):
if not node:
return
if node.val == val:
return (parent, depth)
left_info = dfs(node.left, node, depth+1, val)
if left_info:
return left_info
right_info = dfs(node.right, node, depth+1, val)
if right_info:
return right_info
x_parent, x_depth = dfs(root, None, 0, x)
y_parent, y_depth = dfs(root, None, 0, y)
return x_parent != y_parent and x_depth == y_depth
优化后的算法更加简洁,也更加高效。不仅可以正确地判断x和y是否为堂兄弟节点,还可以避免不必要的遍历,提高代码的效率。
广度优先搜索算法优化
可以对上述算法进行以下优化:
-
如果找到了x和y的信息,就可以直接返回结果,避免继续执行不必要的循环。
-
如果深度已经不同了,就不需要再继续遍历,可以直接返回结果。
以下是优化后的代码:
class Solution:
def isCousins(self, root, x, y):
queue = [(root, None)]
x_info = None
y_info = None
depth = 0
while queue:
depth += 1
for i in range(len(queue)):
node, parent = queue.pop(0)
if node.val == x:
x_info = (parent, depth)
if node.val == y:
y_info = (parent, depth)
if x_info and y_info:
break
if node.left:
queue.append((node.left, node))
if node.right:
queue.append((node.right, node))
if x_info and y_info:
break
return x_info[0] != y_info[0] and x_info[1] == y_info[1] and depth == x_info[1]
由于优化后的代码在找到x和y的信息时就可以直接返回结果,因此效率更高。