DAY30：回溯算法（五）分割回文串+复原IP地址（注意复盘，经典的分割子集问题）

news2025/1/11 2:37:02

文章目录

    • 131.分割回文串
      • 思路
      • 伪代码
        • 重要问题1：如何通过startIndex判断已经切到结束了
        • 重要问题2：为什么[startIndex,i]能够表示当前遍历的子串
        • substr的用法
      • std::string的成员函数
      • `std::string`
      • 完整版
        • debug测试
          • **Line 4: Char 27: error: expected unqualified-id**
          • substr的使用问题: Char 30: error: use of undeclared identifier 'substr'
      • 回文的判断方法
      • 总结+完整树形图
        • 关于剪枝
      • 时间复杂度
    • 93.复原IP地址
      • 思路
      • 伪代码
        • 为什么本题不需要定义两个数组path和result
      • 完整树形图
      • 完整版
      • debug测试：
        • 重要：逻辑错误，必须判断第四个字段是不是存在！
        • 注意insert需要传入迭代器而不是之间传下标
        • 溢出问题：isValue的判断，取整数发现溢出
      • 判断子串合法性
        • 注意累加字符串数值的方法
        • 关于剪枝
      • 时间复杂度

131.分割回文串

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

示例 1：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

提示：

  • 1 <= s.length <= 16
  • s 仅由小写英文字母组成

思路

这道题如果用for循环暴力实现，for的嵌套数量会非常多，导致代码很难写。实际上分割问题和组合问题很像。先得到所有的分割方案，分割方案都放在叶子节点上，再对分割方案是不是回文进行判断。

例如对于字符串abcdef：

  • 组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中再选取第三个…。
  • 切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中再切割第三段…。

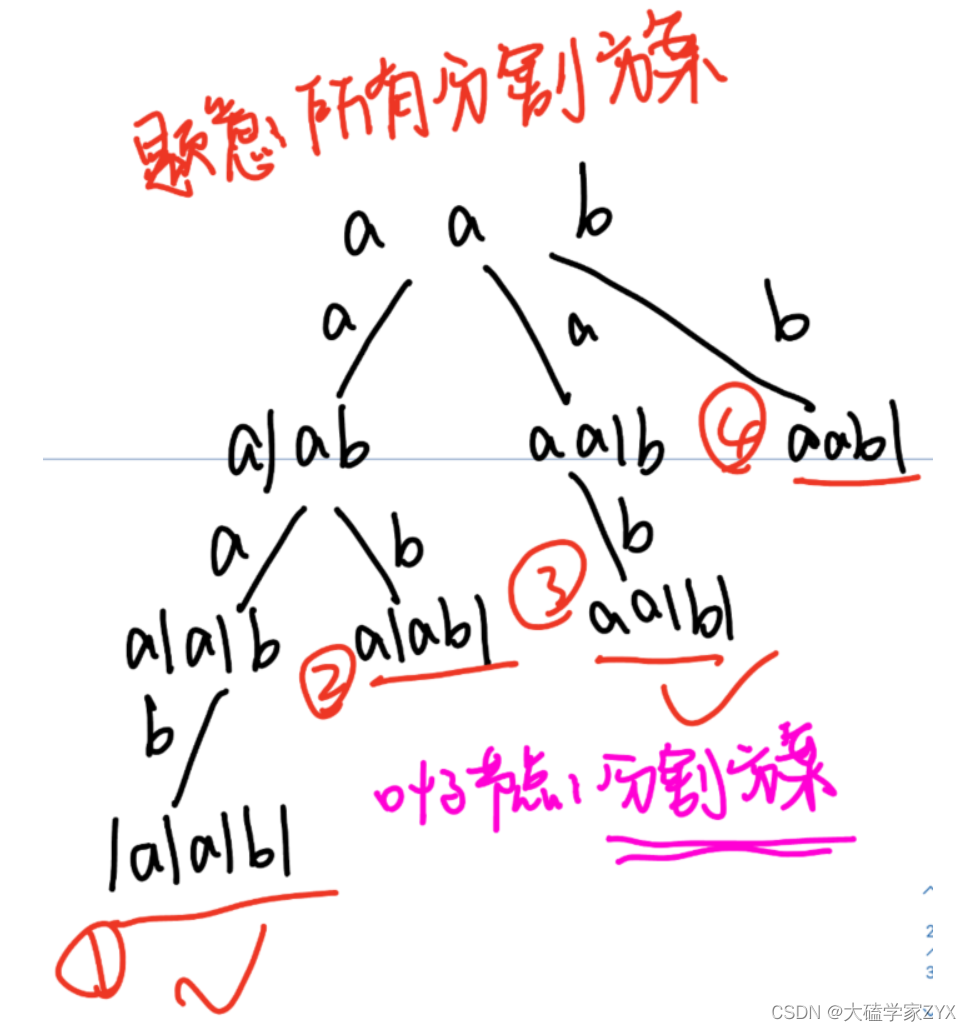
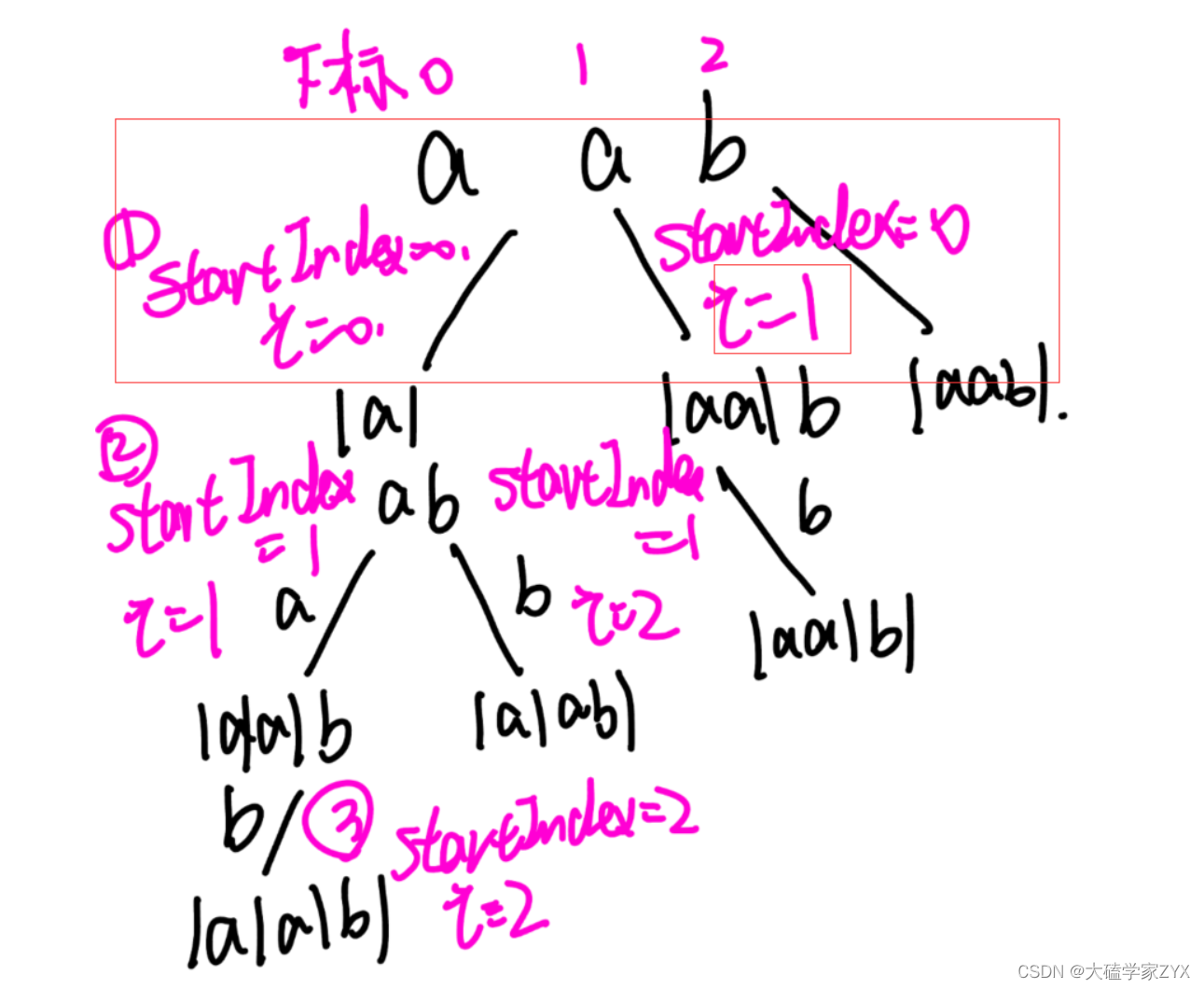
所以切割问题，也可以抽象为一棵树形结构，如下图所示：

注意本题是需要返回分割方案，分割方案意味着每一个叶子节点上应该都是字符串的所有子串的分割情况

如下图，以给出的示例为例，我们最后得到了四种分割方案。（割下去一刀才算这个字符串得到了）

在这里插入图片描述

伪代码

  • 一维数组接收叶子节点，二维数组接收答案
  • 传入参数注意const引用的问题，不想被改变应该传入const string&
  • 本题是在单个集合里面切割，所以需要startIndex控制切割起点，在本题的切割过程中，startIndex就是树形结构里的切割线！
  • 遍历到最后一个的时候就没必要再加分割线了，遍历到最后前面的分割线已经定了
  • 本题是直接在path的时候就判断是不是回文，不是回文直接continue。判断回文逻辑也可以放终止条件里，判断path是不是回文，是再加入result
  • [startIndex,i]这个左闭右闭区间，就是每次搜索的时候子串的范围，i每移动一位，就会有一个新的子串！
void backtracking(vector<int>&path,vector<vector<int>>&result,const string& s,int startIndex){
    //终止条件：切割到最后就算是终止了，在代码里，startIndex就是切割线！
    if(startIndex==s.size()){
        //path.push_back()此时已经不需要往path里面加入结果了，因为遍历到最后一个，前面的所有分割线已经确定了！
        result.push_back(path);
        return;
    }
    //单层搜索
    for(int i = startIndex;i<s.size();i++){
        if(isPalindrome(s,startIndex,i)){//如果[startIndex,i]是回文子串
            //[startIndex,i]加入path里面
            string str = s.substr(startIndex,i-startIndex+1);
            path.push_back()
        }
        else
            continue;
        backtracking(path,result,s,i+1);
        path.pop_back();
    }
    
    
}

重要问题1：如何通过startIndex判断已经切到结束了

下面的示例，第二个a回溯的时候，i已经指向了第二个a，那么i+1自然就指向b。也就是startIndex已经开始切割最后一个了。也就是说，当startIndex=s.size()的时候，也就是此时已经把i+1也就是b传入递归了，说明已经到了叶子节点，可以收集当前遍历节点作为最后一个结果了。

终止条件逻辑如下：

    //终止条件：切割到最后就算是终止了，在代码里，startIndex就是切割线！
    if(startIndex==s.size()){
        //path.push_back()此时已经不需要往path里面加入结果了，因为.size()的地方没有元素
        result.push_back(path);
        return;
    }

终止条件也就是切到了叶子节点，当startIndex遍历到了叶子节点的时候，也就意味着本条分支的path结果已经得到了，因为下标s.size()的地方是没有元素的！

对于字符串 s，下标 s.size() 的地方是没有元素的，它实际上已经超出了字符串的范围。例如，对于字符串 “abc”，下标 0 对应的是 ‘a’，下标 1 对应的是 ‘b’，下标 2 对应的是 ‘c’，而下标 3（等于字符串的长度）已经超出了字符串的范围，它的位置是在 ‘c’ 的后面！因此终止条件，当分割线到了.size()才是正确的。

重要问题2：为什么[startIndex,i]能够表示当前遍历的子串

同样以"aab"为例，我们需要注意的是，同一父节点每一层的从左往右，就是 i 在不断变大。但是同一父节点的情况下，也就是单层的递归内部，startIndex是保持不变的！

递归for循环逻辑如下：

    //单层搜索
    for(int i = startIndex;i<s.size();i++){
        if(isPalindrome(s,startIndex,i)){//如果[startIndex,i]是回文子串
            //[startIndex,i]加入path里面
            string str = s.substr(startIndex,i-startIndex+1);
            path.push_back()
        }
        else
            continue;
        backtracking(path,result,s,i+1);
        path.pop_back();
    }

例如第一层的递归内部，startIndex一直都是0！只有同一父节点下面的i会发生变化！因此，在每个父节点下面，[startIndex,i]都会表示当前遍历到的子串！

在这里插入图片描述

substr的用法

substr 是 string 类的一个成员函数，它的功能是从字符串中取出一个子串。

它有两个参数，第一个参数 pos 表示子串的开始位置，第二个参数 len 表示子串的长度。

具体来说，s.substr(startIndex, i - startIndex + 1); 这行代码的功能是取出字符串 s 中从下标 startIndex 开始，长度为 i - startIndex + 1 的子串。

例如，对于字符串 “abc”，如果 startIndex 为 0，i 为 1，那么 s.substr(startIndex, i - startIndex + 1); 就会取出 “ab” 这个子串。

std::string的成员函数

std::string

参见：std::basic_string

  • 重载了赋值运算符 +，当 + 两边是 string/char/char[]/const char* 类型时，可以将这两个变量连接，返回连接后的字符串（string）。
  • 赋值运算符 = 右侧可以是 const string/string/const char*/char*。
  • 访问运算符 [cur] 返回 cur 位置的引用。
  • 访问函数 data()/c_str() 返回一个 const char* 指针，内容与该 string 相同。
  • 容量函数 size() 返回字符串字符个数。
  • find(ch, start = 0) 查找并返回从 start 开始的字符 ch 的位置；rfind(ch) 从末尾开始，查找并返回第一个找到的字符 ch 的位置（皆从 0 开始）（如果查找不到，返回 -1）。
  • substr(start, len) 可以从字符串的 start（从 0 开始）截取一个长度为 len 的字符串（缺省 len 时代码截取到字符串末尾）。
  • append(s) 将 s 添加到字符串末尾。
  • append(s, pos, n) 将字符串 s 中，从 pos 开始的 n 个字符连接到当前字符串结尾。
  • replace(pos, n, s) 删除从 pos 开始的 n 个字符，然后在 pos 处插入串 s。
  • erase(pos, n) 删除从 pos 开始的 n 个字符。
  • insert(pos, s) 在 pos 位置插入字符串 s。
  • std::string 重载了比较逻辑运算符，复杂度是O(N)的。

注意：substr这种函数， 是 string 类的成员函数，必须使用 . 运算符来调用！不能单独使用！

正确的写法是 s.substr(startIndex,i-startIndex+1)。

完整版

  • string最好定义为const
class Solution {
public:
	bool isPalindrome(const string& s,int start,int end){
        int i=start;
        int j=end;
        for(;i<j;i++,j--){ //i<j放在最后面会失效
            if(s[i]!=s[j])
                return false;
        }
        return true;
    }
    
    void backtracking(vector<string>&path,vector<vector<string>>&result,const string& s,int startIndex){
        //终止条件
        if(startIndex==s.size()){
            result.push_back(path);//加入result中
            return;
        }
        //单层搜索
        for(int i=startIndex;i<s.size();i++){
            //判断[start,i]这个区间的子串，是不是回文串
            if(isPalindrome(s,startIndex,i)){
                //如果是，将子串加入path
                string str = s.substr(startIndex,i-startIndex+1);
                path.push_back(str);
                //递归
                backtracking(path,result,s,i+1);
                //回溯
                path.pop_back();
            }
        }
        
    }
    
    vector<vector<string>> partition(string s) {
		vector<string>path;
        vector<vector<string>>result;
        int startIndex=0;
        backtracking(path,result,s,startIndex);
        return result;
    }
};

debug测试

Line 4: Char 27: error: expected unqualified-id

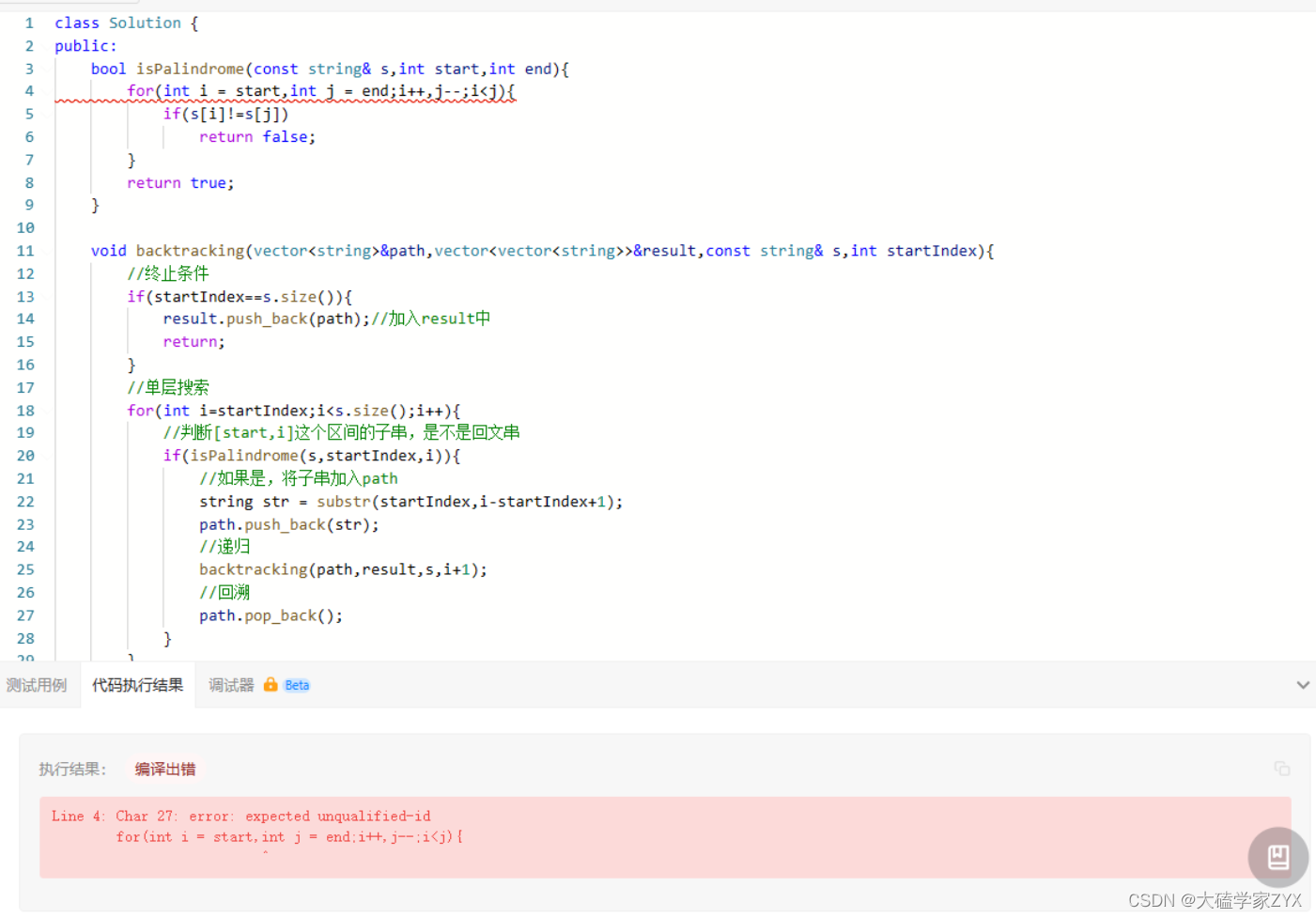
在这里插入图片描述
这个错误提示是由于在 C++ 中的 for 循环的初始化部分不支持声明多个类型不同的变量。在你的代码中，i 和 j 的声明方式是不正确的。应该分开声明，并分别赋值。这样修改后的代码如下：

另，i<j不能写在最后面，结束条件一旦写在最后面就没有意义了！

	bool isPalindrome(const string& s,int start,int end){
        int i = start;
        int j = end;
        for(; i < j; i++, j--){
            if(s[i] != s[j])
                return false;
        }
        return true;
    }
substr的使用问题: Char 30: error: use of undeclared identifier ‘substr’

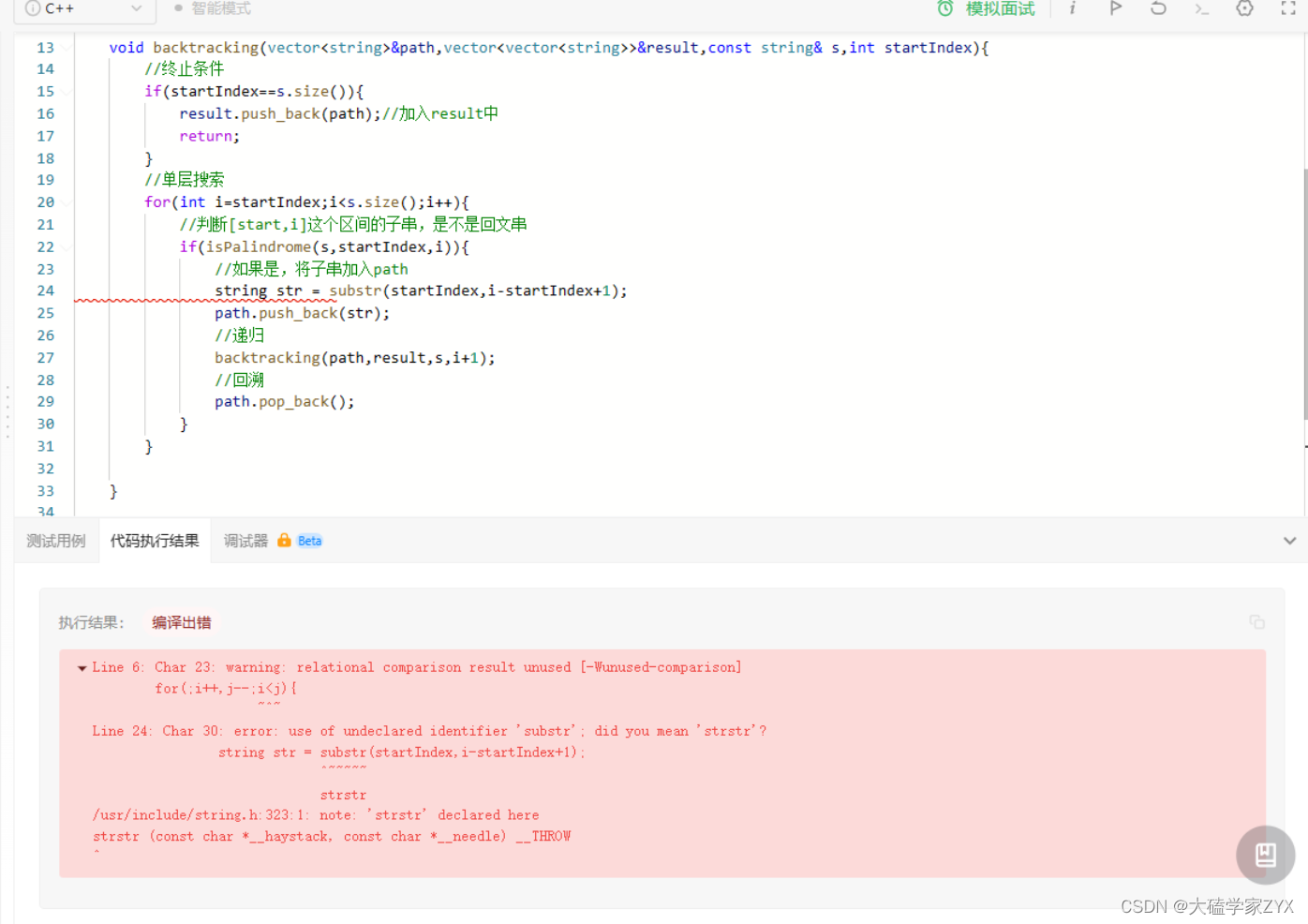
在这里插入图片描述
注意：substr 是 string 类的成员函数，必须使用 . 运算符来调用，不能单独使用。正确的写法是 s.substr(startIndex,i-startIndex+1)

string str = s.substr(startIndex, i - startIndex + 1);

回文的判断方法

本题回文是单独的子函数isPalindrome()实现的。使用双指针法来判断回文

回文的参数是原字符串，字符串起点下标和字符串终点下标

bool isPalindrome(string s,int start,int end){
    for(int i=start,int j=end;i++,j--;i<j){
        if(s[i]!=s[j]){
            return false;
        }
    }
    return true;
}

双指针是一种很重要的思路，可以参考代码随想录里双指针的总结，复习一下这种思路：

代码随想录 (programmercarl.com)

总结+完整树形图

本题难点：

1.确定终止条件，终止条件就是分割线startIndex==s.size()，因为s.size()无任何元素，所以结束

2.要明确一点，[startIndex，i]就是每一层分割的子串！因为每一层的startIndex是不变的，而i是不断递增一直到字符串结束的！每一层的i，都会从startIndex开始，一直增加到i=s.size()-1为止！

以"aab"字符串为例，每一层的递归和参数情况如下：

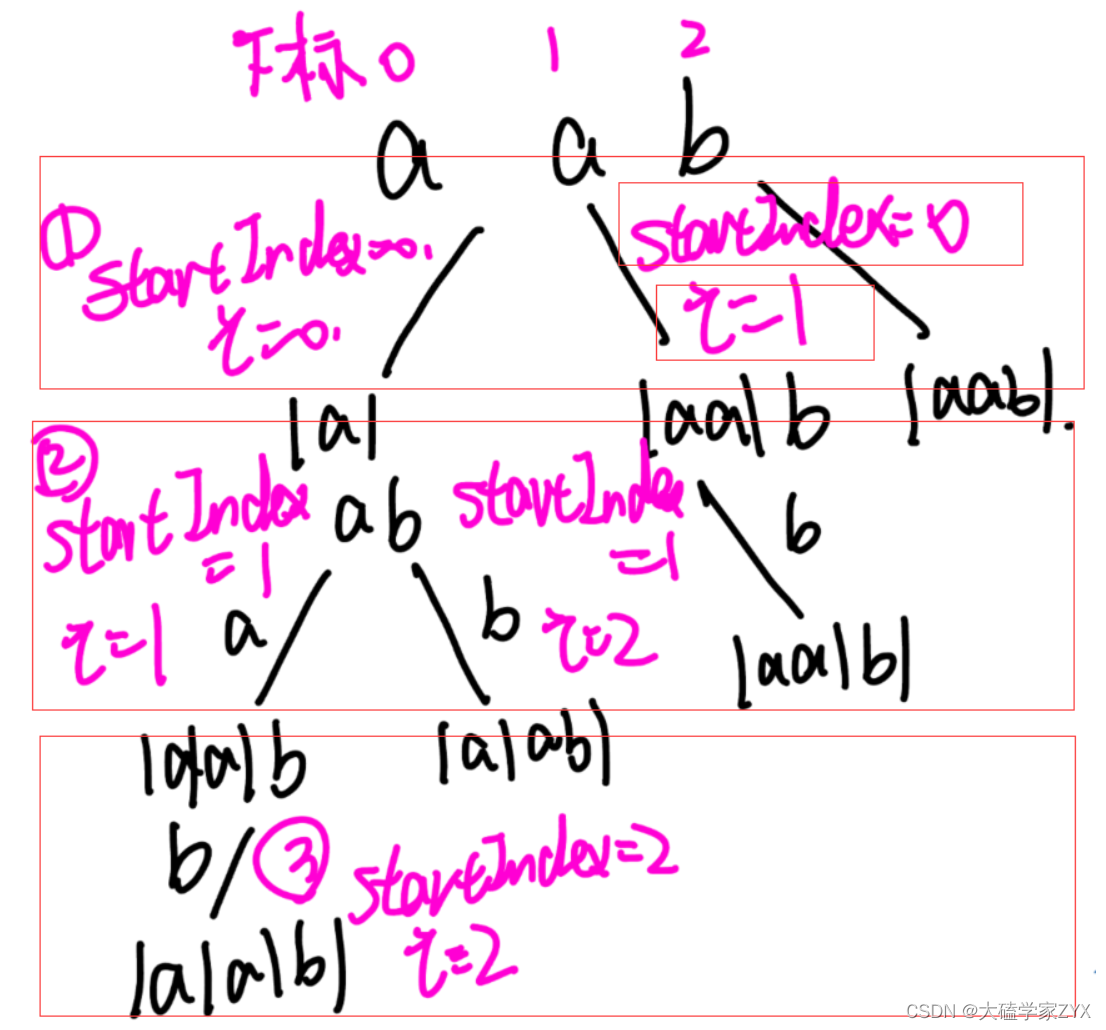
在这里插入图片描述
画出树形图，标出所有参数，这道题逻辑就比较清楚了。

关于剪枝

本题也不需要剪枝，因为本题不存在无效的搜索路径，回文子串的切割必须要切割到最后一位才能判定！

时间复杂度

这个算法的时间复杂度是 O(n * 2^n)，其中 n 是字符串 s 的长度。

这是因为这个问题是一个典型的子集问题，类似于幂集问题，对于长度为 n 的字符串 s，存在 2^n 种可能的子集，这是因为每个字符都可以选择包含或者不包含在子集中。对于每个子集，我们都需要花费 O(n) 的时间复杂度来生成这个子集。所以总的时间复杂度是 O(n * 2^n)。

这也符合子集问题大都是c^k的时间复杂度的特性。

93.复原IP地址

  • 分割子串的左右区间，主要是利用了本层递归（同一父节点）startIndex不变，而i是递增的这一点。

  • 分割子串类型题目，判断子串的合法性最好单独写一个函数！

  • 本题限制了4个字段，判断字段是不是存在的标准，是字段左边界是否<=字段右边界！

有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 ‘.’ 分隔。

  • 例如：“0.1.2.201” 和 “192.168.1.1” 是 有效 IP 地址，但是 “0.011.255.245”、“192.168.1.312” 和 “192.168@1.1” 是 无效 IP 地址。

给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。

示例 1：

输入：s = "25525511135"
输出：["255.255.11.135","255.255.111.35"]

示例 2：

输入：s = "0000"
输出：["0.0.0.0"]

示例 3：

输入：s = "101023"
输出：["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]

提示：

  • 1 <= s.length <= 20
  • s 仅由数字组成

思路

本题不仅要进行切割，还要对切割的段进行合法性的判断。

回溯算法暴力枚举每一种情况，下面以25525511为例，画出树形图：

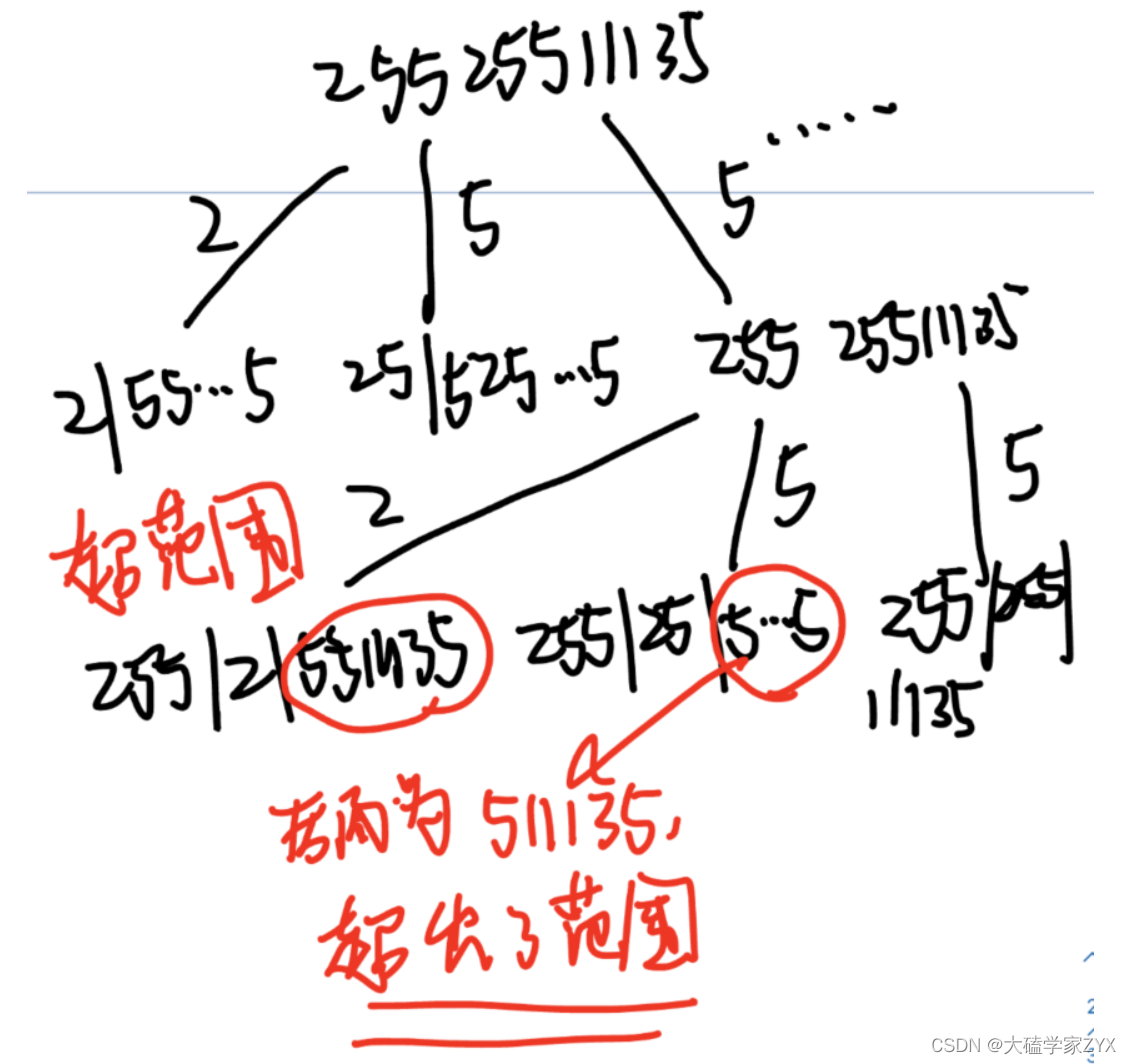
在这里插入图片描述
我们可以看出，这个例子里面有很多子集都超出了范围，例如切割255.25后面的部分的时候，剩余511135，511这个数字大于255，所以直接超出范围被舍弃。

我们需要在切割子串的同时，判断子串是否合法。

伪代码

  • IP需要加上三个逗号，终止条件可以通过当前逗号的个数来进行计算。逗号数目实际上决定了树的深度，三个逗号说明无需继续切割了！
  • 合法性判断也是单独写函数，这类分割问题，都建议判断合法性的地方建议单独写函数！
  • 分割线，是i选到哪里，分割线就到哪里，因此分割子串的右区间是i，左区间是startIndex! 分割子串的左右区间，主要是利用了本层递归（同一父节点）startIndex不变，而i是递增的这一点。
void backtracking(vector<string>&result,string& s,int pointSum,int startIndex){
    //终止条件
    if(pointSum==3){
        //已经有三个逗号了，需要终止，3决定了树的深度
        //对最后一段进行合法性判断
        if(isValue(s,startIndex,s.size()-1)){
            result.push_back(s);
            return;
        }
    }
    //单层搜索
    for(int i=startIndex,i<s.size();i++){
        //判断每一层递归中子串的合法性，子串也就是[startIndex,i]
        if(isValue(s,startIndex,i)){
            //字符串s进行改造，如果i符合，就在i+1加上逗号
            s.insert(s.begin()+i+1,'.');
            pointSum += 1;
            //递归，注意此时i+1被处理了逗号，应该是i+2！
            backtracking(result,s,pointSum,i+2);
            //回溯，注意之前插入的逗号也需要删掉！
            pointSum -= 1;
            s.erase(s.begin()+i+1,'.');
        }
    }        
}

为什么本题不需要定义两个数组path和result

仔细看题目，本题的返回是["255.255.11.135","255.255.111.35"]，相当于是直接返回一个string的一维数组即可。也就是说，我们可以直接对传入的s进行插入操作，加上'.'，如果s符合要求，那么就可以直接返回s。

这样的话，就不需要每一次都使用path保存路径，因为结果已经在被修改的s里面了。

本题与切割回文串的区别就在于，本题可以直接对字符串进行操作，因为输出的格式本身就不需要存储，返回格式直接就是vector<string>。

完整树形图

本题依旧是利用了startIndex在一层递归内不变，i在一层递归内在上一层递归基础上叠加（因为递归传入的是上一层的i+1）**的特性，用[startIndex,i]表示了每一层的所有切割结果。

比如图中的第二层递归的第三个分支255|25511135，此时startIndex=1，而i是基于父节点的的for循环结束位置i=2的位置继续进行叠加，也就是i=3。

在这里插入图片描述

完整版

  • 注意s.erase的用法，力扣的cpp版本只需要传入下标即可。
  • 注意本题限制了是四个字段，所以终止条件必须同时判定第四个字段是不是存在！判定是否存在的标准就是字段左边界是否<=字段右边界！
class Solution {
public:
    bool isValue(string& s,int start,int end){
        //注意传入的是字符而不是数字
        if(s[start]=='0'&&start!=end){
            return false;
        }
        int num=0;
        for(int i=start;i<=end;i++){
            if(s[i]>'9'||s[i]<'0'){
                return false;
            }
            num=num*10+(s[i]-'0');
            //移到里面否则会溢出
            if(num>255){
            return false;
             }
        }
        
        return true;
    }
    void backtracking(vector<string>&result,string& s,int pointSum,int startIndex){
        //终止条件
        if(pointSum==3){
            if(isValue(s,startIndex,s.size()-1)&&startIndex<=s.size()-1){
                result.push_back(s);
            }
            return;
        }
        //单层搜索
        for(int i=startIndex;i<s.size();i++){
            //判断[startIndex,i]子串是否合法
            if(isValue(s,startIndex,i)){
                s.insert(s.begin()+i+1,'.');
                pointSum += 1;
                backtracking(result,s,pointSum,i+2);
                s.erase(s.begin()+i+1);
                pointSum -= 1;
            }
            else
                break;
        }
    }
    vector<string> restoreIpAddresses(string s) {
		vector<string>result;
        int startIndex=0;
        int pointSum=0;
        backtracking(result,s,pointSum,startIndex);
        return result;
    }
};

debug测试：

重要：逻辑错误，必须判断第四个字段是不是存在！

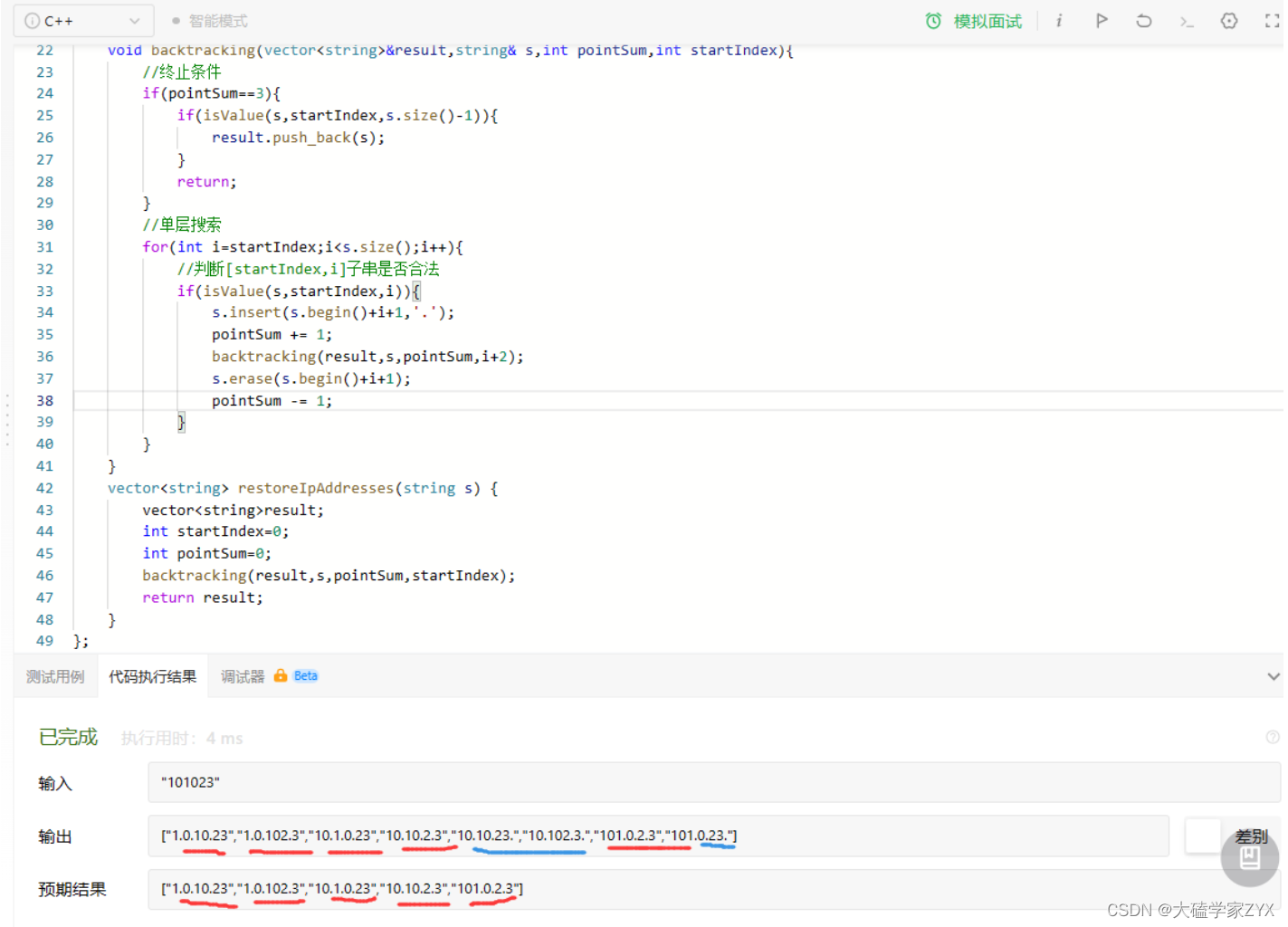
在这里插入图片描述
预期输出出现了三个字段的字符串。出现三个字段就是因为当逗号有三个的时候，会出现[10,102,3]这样的组合，这就是因为第四个字段实际上不存在，就会出现这样的错误。

修改方式是终止同时，判断第四个是否存在，第四个的下标开头是startIndex, 而字符串末尾是s.size()-1，因此只要startIndex<=s.size()-1,第四个字段就是存在的！

加上以上条件之后输出正确。

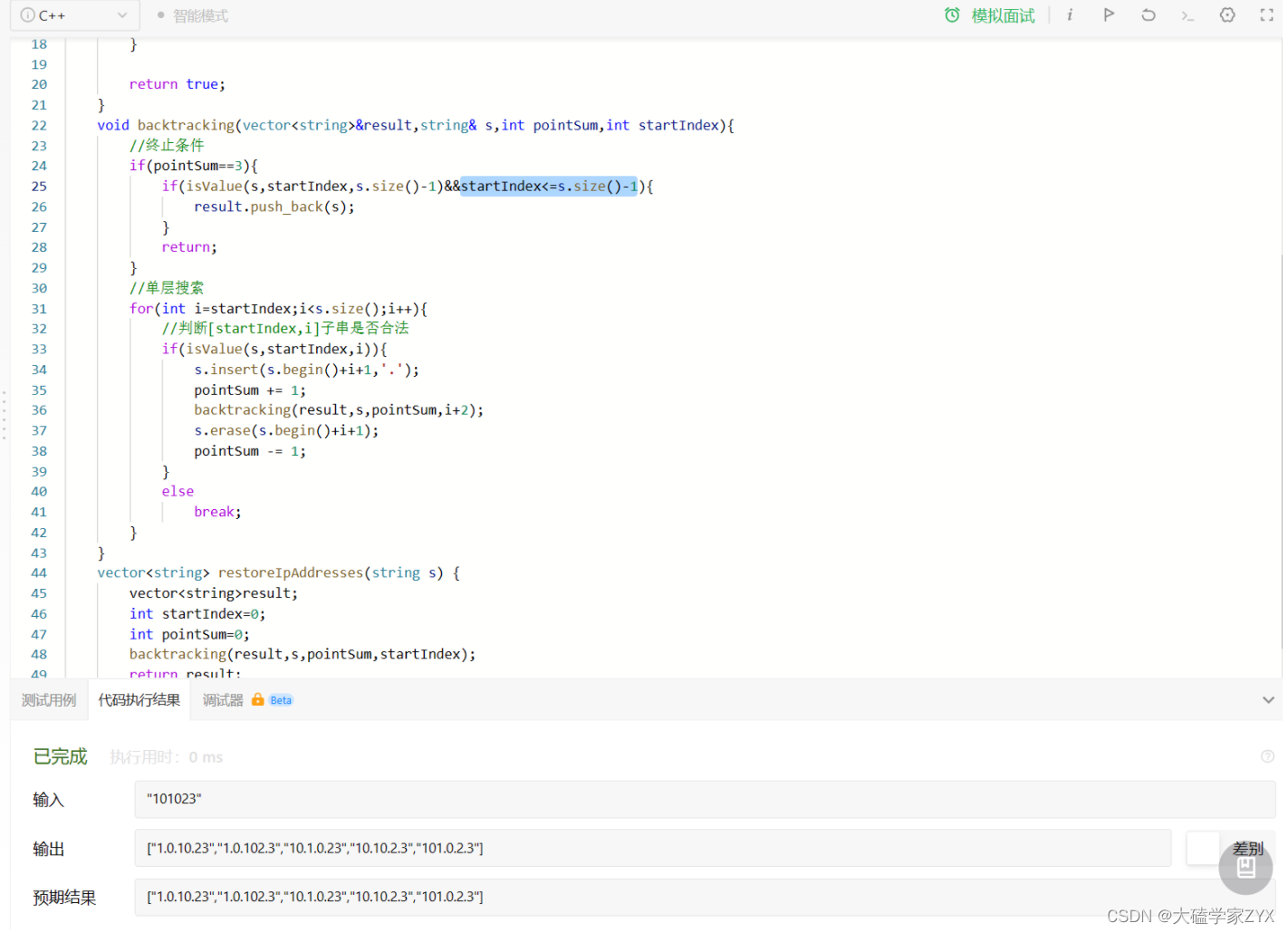
在这里插入图片描述

注意insert需要传入迭代器而不是之间传下标

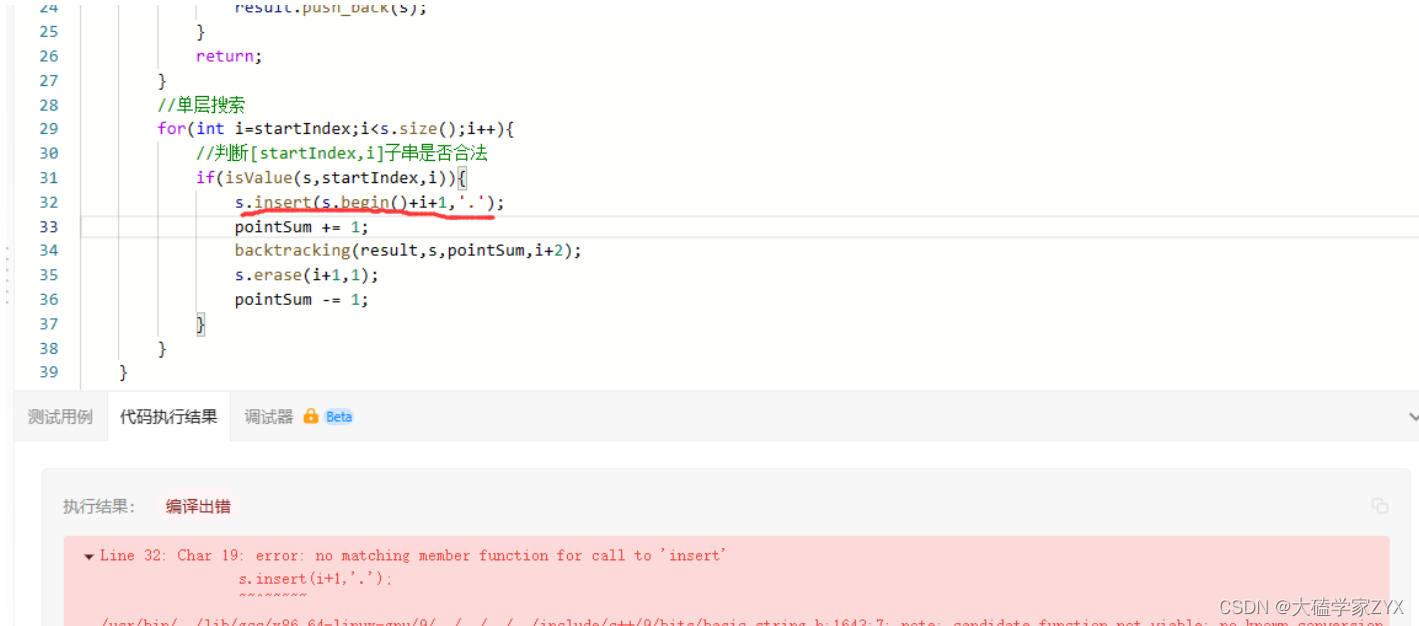
在这里插入图片描述
insert需要传入s.begin()+i+1，而不是直接传i+1！

溢出问题：isValue的判断，取整数发现溢出

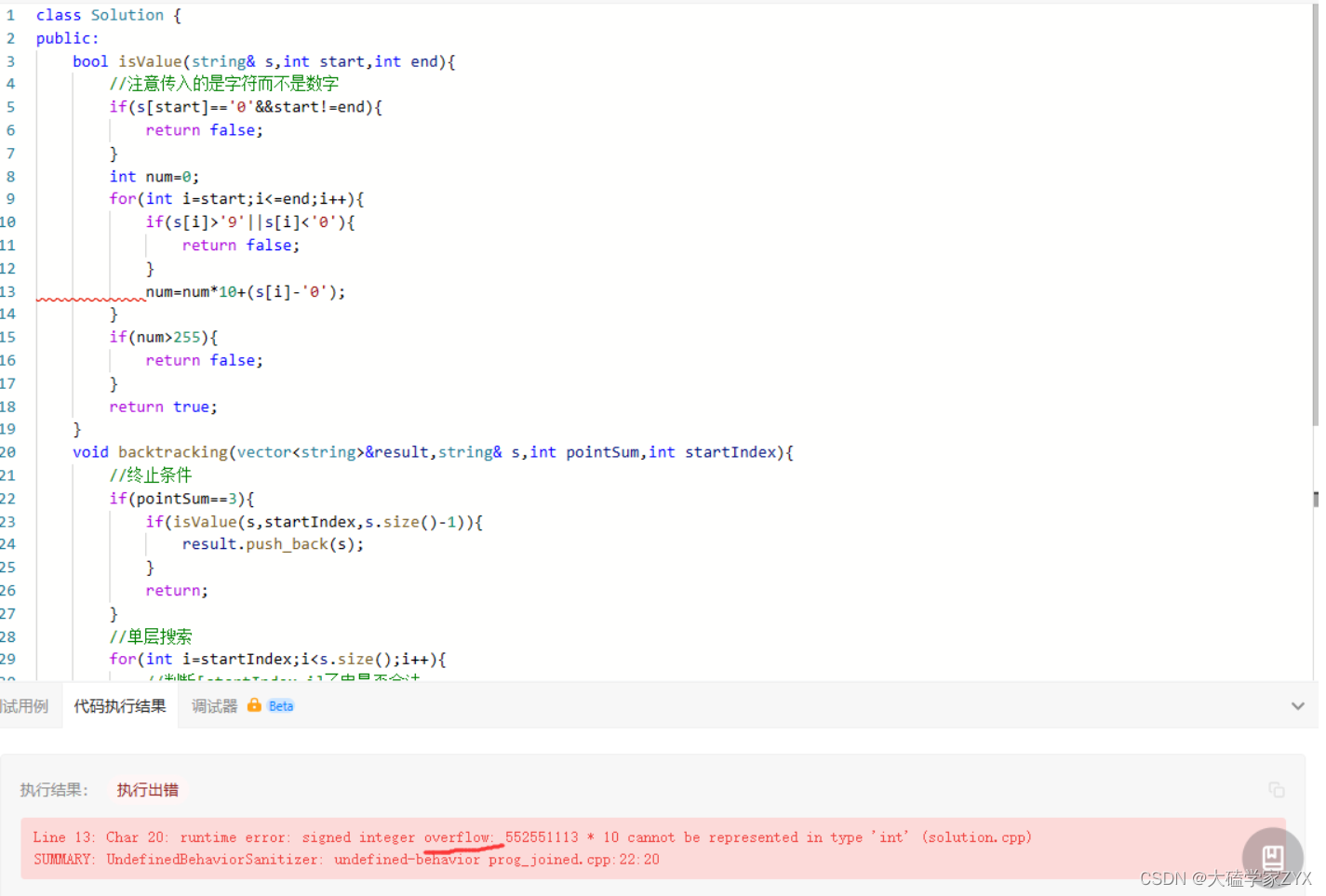
在这里插入图片描述
这个问题可以通过把if判断移到for循环内部解决，因为我们没必要得到完整的数字！只要当前数字超过255，已经可以return了！

修改结果：

        for(int i=start;i<=end;i++){
            if(s[i]>'9'||s[i]<'0'){
                return false;
            }
            num=num*10+(s[i]-'0');
            //移到里面否则会溢出
            if(num>255){
            return false;
             }
        }
        return true;
    }

判断子串合法性

  • 单独一个0是合法的，但是有先导0是不合法的
  • 非正整数字符不合法
  • 整段数字>255不合法
bool isValue(string& s,int start,int end){
    if(s[start]=='0'&&start!=end){
        return false;
    }
    int num=0;
    //注意循环从start和end开始
    for(int i=start;i<=end;i++){
        //遍历判断有没有非整数字符
        if(s[i]>'9'||s[i]<'0'){
            return false;
        }
        //遍历同时，累计传入字符串中的数字
        num = (s[i]-'0')+num*10;//s[i]-'0'是本身的数字，num*10是在累计个位数和十位数！
    }
    if(num>255){
        return false;
    }
    //前面所有情况都没return，说明通过
    return true;
}

注意累加字符串数值的方法

考虑字符串 “123”。它表示的是整数123，这个整数是由3个数字构成的，从左到右依次是1、2和3。它们分别表示百位、十位和个位。如果我们用 num 来表示这个整数，那么它的构造过程是这样的：

  1. num 初始值为0。然后我们遍历到字符 ‘1’，s[i]-'0' 的值就是1，num*10 的值就是0，所以 num = 1+0 = 1。
  2. 接下来我们遍历到字符 ‘2’，s[i]-'0' 的值就是2，num*10 的值就是10，所以 num = 2+10 = 12。
  3. 最后我们遍历到字符 ‘3’，s[i]-'0' 的值就是3，num*10 的值就是120，所以 num = 3+120 = 123。

这样我们就把字符串 “123” 转换成了整数 123。

逻辑如下：

	int num=0;
    //注意循环从start和end开始
    for(int i=start;i<=end;i++){
        //遍历时，累计传入字符串中的数字
        num = (s[i]-'0')+num*10;//s[i]-'0'是本身的数字，num*10是在累计个位数和十位数！
    }

num = (s[i]-'0')+num*10; 的意义是，将当前处理的字符 s[i] 转换为对应的数字，然后加到 num*10 上。num*10 的操作实际上是把 num 已有的值左移一位，为新的数字让出位置。

这样，当遍历到下一个字符时，原先的数值就被正确地提升到更高的位置（个位变十位，十位变百位等），新的数字则被添加到个位。使用加法操作而不是乘法操作，主要就是为了添加数字的时候能够正确的左移！因为最开始遍历的是最高位的数字！

关于剪枝

同样本题也不太好做剪枝，因为本题也没有无效的搜索路径。

时间复杂度

例如数字 255 可以分割为为 2 | 55、25 | 5 、 255 | 三种，一个位置的数字最多三位（对应三种分割方法），本题是IP地址，一共四个位置，因此时间复杂度是O(3^4)。

这也符合子集问题大都是c^k的时间复杂度的特性。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/690717.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MySQL------事务并发问题和解决办法

MySQL------事务并发问题和解决办法

一、事务并发问题 1. 脏读 含义&#xff1a;在事务过程中&#xff0c;A事务还未提交&#xff0c;B事务就读到了A事务未提交的数据。 一个事务正在对一条记录做修、改&#xff0c;在这个事务完成并提交前&#xff0c;这条记录的数据就处于不一致状态&#xff1b;这时&#xff0c…
阅读更多...
PHP 文心千帆API接口对接

PHP 文心千帆API接口对接

一&#xff1a;API 调用流程简介 创建一个智能云应用。根据实际需求创建智能云应用。创建成功后&#xff0c;获取AppID、API Key、Secret Key 等信息。API 授权。对应用的 AppID 进行授权。获取接口访问凭证 access_token 。根据第1步获取的 API Key 和 Secret Key &#xff0c…
阅读更多...
外观模式（Facade）

外观模式（Facade）

定义 外观是一种结构型设计模式&#xff0c;能为程序库、框架或其他复杂类提供一个简单的接口。 前言 1. 问题 假设你必须在代码中使用某个复杂的库或框架中的众多对象。正常情况下&#xff0c;你需要负责所有对象的初始化工作、管理其依赖关系并按正确的顺序执行方法等。 …
阅读更多...
centos 手动下载包安装elasticsearch8.7.0, 并设置密码访问

centos 手动下载包安装elasticsearch8.7.0, 并设置密码访问

访问下载网站 Elasticsearch 8.7.0 | Elastic 进入centos , 创建目录es mkdir /opt/es cd /opt/es wget https://artifacts.elastic.co/downloads/elasticsearch/elasticsearch-8.7.0-linux-x86_64.tar.gz 3、解压目录 es870 tar -zxvf elasticsearch-8.7.0-linux-x86_64.tar…
阅读更多...
二叉树的堂兄弟节点——深度优先搜索+广度优先搜索

二叉树的堂兄弟节点——深度优先搜索+广度优先搜索

二叉树的堂兄弟节点 题目描述 在二叉树中&#xff0c;根节点位于深度 0 处&#xff0c;每个深度为 k 的节点的子节点位于深度 k1 处。 如果二叉树的两个节点深度相同&#xff0c;但 父节点不同 &#xff0c;则它们是一对堂兄弟节点。 我们给出了具有唯一值的二叉树的根节点 …
阅读更多...
实现分布式事务的新标杆：RocketMQ的全面解析与应用指南

实现分布式事务的新标杆：RocketMQ的全面解析与应用指南

在分布式系统中&#xff0c;实现事务的一致性和可靠性是一项重要的挑战。本文将详细介绍如何利用 RocketMQ 的半消息机制来实现分布式事务&#xff0c;并提供具体的代码示例和最佳实践。 1. 引言 在分布式系统中&#xff0c;事务处理是一项复杂而关键的任务。传统的 ACID 事务…
阅读更多...
基于SpringCloud微服务毕业论文管理系统设计与实现

基于SpringCloud微服务毕业论文管理系统设计与实现

一、概述 1.1 课题背景及意义 随着学校不断扩大和学生人数的猛增，关于各类教学信息也越来越多。毕业论文的管理也成为了不可避免的一道关卡，学生需要及时获取论文相关进度，学校的管理者要求能方便对论文进行处理。基于这些需求，开发一个实用的微服务管理系统，以满足双方…
阅读更多...
13-使用调度框架quartz，为系统增加定时调度功能

13-使用调度框架quartz，为系统增加定时调度功能

1 、创建后端模块batch 1.1、创建maven项目 1.2、pom.xml文件中导入依赖 <dependencies><!-- common--><dependency><groupId>com.wei</groupId><artifactId>common</artifactId></dependency><!-- 热部署…
阅读更多...
电磁兼容常用测量单位及转换关系 dB、dBm、dBw、dBμV、dBmV、dBV、dBA等单位介绍

电磁兼容常用测量单位及转换关系 dB、dBm、dBw、dBμV、dBmV、dBV、dBA等单位介绍

目 录 摘要分贝简介分贝在EMC测试中电磁兼容常用测量单位常用线性单位的对数转换单位间转换基于50Ω额定阻抗的电压、电流和功率单位间的换算基于50Ω额定阻抗的场强单位间的换算 单位换算的应用参考文献总结 摘要 为获得更大的相对幅度显示范围&#xff0c;电磁兼容测试常使用…
阅读更多...
Graalvm Native Image 元数据适配

Graalvm Native Image 元数据适配

Graalvm Native Image 元数据适配 本文章主要叙述在 Java 应用适配 Graalvm Native Image 中的步骤和遇到的一些问题&#xff01;因为 Graalvm 官方文档相关概念叙述过于简单。基本靠问才能知道些许有用信息。所以写此文章。 关于 Graalvm 基础知识的相关学习&#xff0c;可以…
阅读更多...
部署 LAMP平台Linux,Apache,MySQL ,PHP源码编译安装

部署 LAMP平台Linux,Apache,MySQL ,PHP源码编译安装

目录 一、.LAMP简介与概述 1.LAMP平台概述 2. 构建LAMP平台顺序 3. 编译安装的优点 4. 各组件作用 5. 数据流向 二、编译安装Apache httpd服务 1.关闭防火墙&#xff0c;将安装Apache所需软件包传到/opt目录下 2.安装环境依赖包 3.配置软件模块 4.编译及安装 5.优…
阅读更多...
chatgpt赋能python：Python获取父类：探究继承关系的技巧

chatgpt赋能python：Python获取父类：探究继承关系的技巧

Python获取父类&#xff1a;探究继承关系的技巧 Python是一种高级编程语言&#xff0c;它被广泛用于Web开发、数据分析、人工智能等领域。Python的面向对象编程是其特色之一。在面向对象编程中&#xff0c;我们经常需要使用继承关系来定义不同类之间的关系。在这篇文章中&…
阅读更多...
小程序学习(一):基本知识点笔记

小程序学习(一):基本知识点笔记

1.小程序与普通网页开发的区别 1.运行环境不同 网页运行在浏览器环境中 小程序运行在微信环境中 2.API不同 由于运行环境的不同,小程序无法调用DOM和BOM的API。 但是,小程序中可以调用微信环境提供的各种API,例如:地理定位、扫码、支付... 3.开发模式不同 网页的开发模式:浏览器…
阅读更多...
C语言笔记-4 输入输出

C语言笔记-4 输入输出

目录 输入输出简单举例scanf()getchar()putchar()puts()gets() 标准文件%d 格式化输出整数%f 格式化输出浮点型数据 getchar() & putchar() 函数gets() & puts() 函数scanf() 和 printf() 函数 输入输出 简单举例 scanf() 空格、回车也是字符&#xff0c;下面情况也…
阅读更多...
APP盲盒系统开发前端后台详细功能讲解

APP盲盒系统开发前端后台详细功能讲解

一、栏目 功能 说明 登录注册 注册 输入手j号&#xff0c;获取验zm&#xff0c;输入密m 密码登录 手机号密码 忘记密码 输入手j号&#xff0c;获取y证m&#xff0c;输入新m码 底部导航 开盲盒、寄售中心、商城、个人中心 开盲盒 显示盲盒 可滑动更换其他盲盒 立即开盒 点…
阅读更多...
从程序员到架构师——数据持久化层场景

从程序员到架构师——数据持久化层场景

全文摘自&#xff1a;从程序员到架构师&#xff08;王伟杰著&#xff09; 购买链接&#xff1a;https://item.jd.com/13626926.html 程序员之间的能力差异在哪里&#xff1f;如果是学技术&#xff0c;大家可以阅读同样的书籍和网络文章&#xff0c;为什么还会造成最终专业能力的…
阅读更多...
SC7515运算放大器(OPA)可pin对pin兼容AD8138

SC7515运算放大器(OPA)可pin对pin兼容AD8138

对于一般运算放大器&#xff0c;SC7515 在差分信号处理方面获得了巨大进步。SC7515 即可以用作单端至差分放大器或也可以差分至差分放大器&#xff0c;像运算放大器一样易于使用&#xff0c;并且大大简化了差分信号放大与驱动。可pin对pin兼容AD8138。该放大器输入噪声低、-3 d…
阅读更多...
Spring之BeanFactory与ApplicationContext区别、实例化Bean的三种⽅式、延迟加载(lazy-Init )

Spring之BeanFactory与ApplicationContext区别、实例化Bean的三种⽅式、延迟加载(lazy-Init )

Spring IoC进阶 IOC之BeanFactory与ApplicationContext区别启动 IoC 容器的方式 实例化Bean的三种⽅式使用无参构造方法实例化工厂静态方法实例化工厂实例方法实例化 Spring IOC之延迟加载(lazy-Init )Bean的延迟加载&#xff08;延迟创建&#xff09;应用场景 IOC之BeanFactor…
阅读更多...
案例分享|梅雨季的机房湿度问题如何解决？

案例分享|梅雨季的机房湿度问题如何解决？

6月底&#xff0c;和Q3的KPI一起赶来的是南方的梅雨季。 持续不断的降雨&#xff0c;使空气湿度一度高达75%-80%&#xff0c; 南方人正式开启高温酷暑下的桑拿模式。 高温高湿除了带来体感不适&#xff0c;还会导致心情抑郁、烦燥、易疲倦...... 毕竟&#xff0c;与此强相关…
阅读更多...
Sentinel spring的全局异常处理器，导致熔断规则(异常数规则)失效解决方案

Sentinel spring的全局异常处理器，导致熔断规则(异常数规则)失效解决方案

最近在使用sentinel过程中发现&#xff0c;如果使用springboot的RestControllerAdvice全局异常捕获&#xff0c;那么设置sentinel的异常数熔断规则就会失效&#xff0c;去github上看sentinel的Issues发现已经有人提过这问题&#xff0c;官方也是没有正面回复 官方文档更不用说&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023