一、有向图的拓扑序列

• 有向图的拓扑序列就是图的广度优先遍历的一个应用。

1. 拓扑序列

• 若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑序列。（起点在终点的前面）
• 拓扑序列是针对有向图，无向图是没有拓扑序列的。
• 有向无环图一定是拓扑序列，有向有环图一定不是拓扑序列。
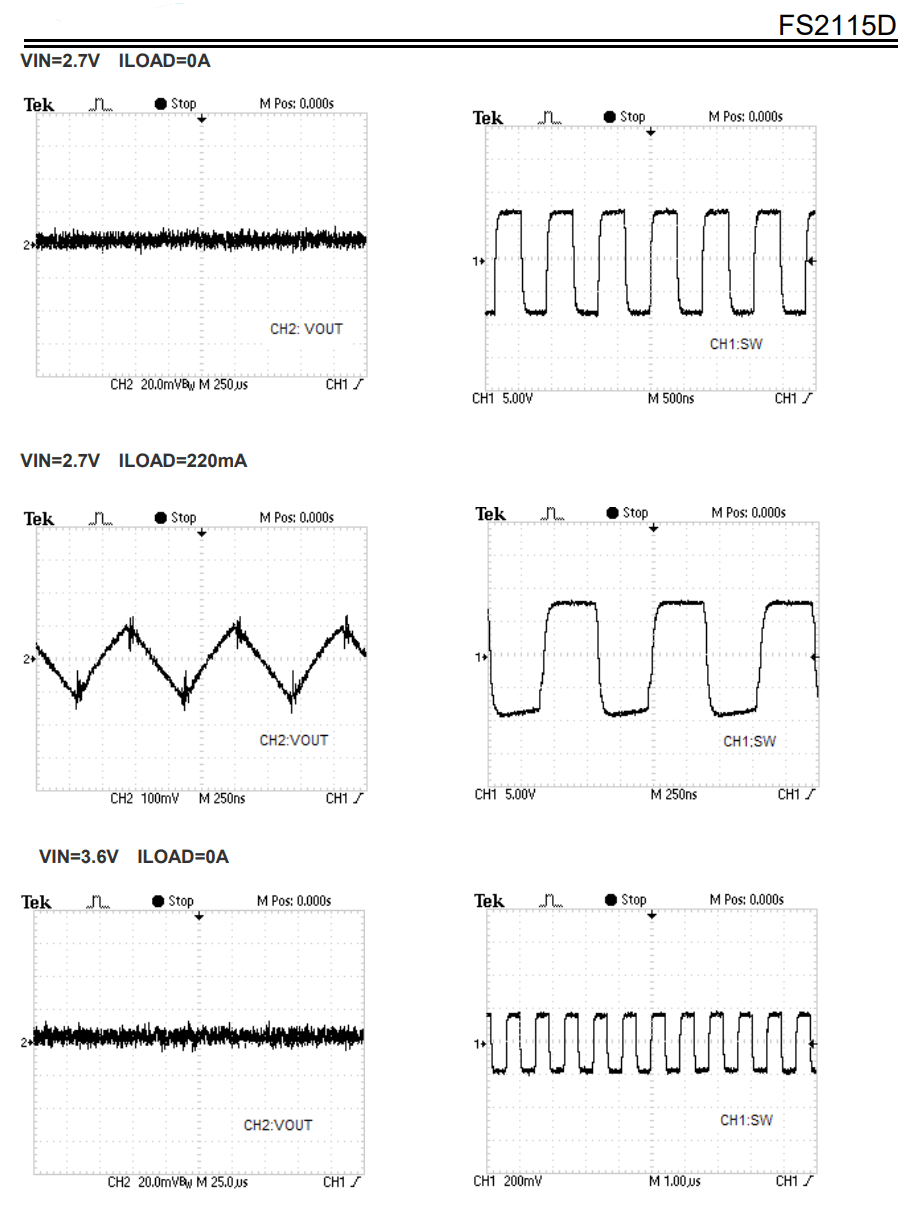
• 例如下图，由于 c 指向了 a ，所以该图不是拓扑序列。

• 同样的例子，由于 d 指向了 b ，所以该图也不是拓扑序列。

2. 拓扑排序

• 入度是指被其他点指向的数量。
• 出度是指指向其他点的数量。
• 举例说明：

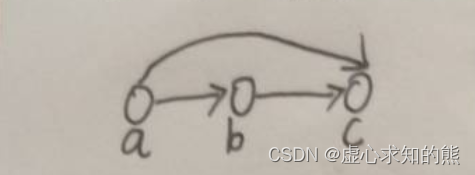
• 由上图可知，a 指向 b 和 c ，b 被 a 指向，并且指向 c ，c 被 a 和 b 指向。
• 因此，a、b、c 的入度和出度分别为：

节点	入度	出度
a	0	2
b	1	1
c	2	0

• 因此，所有入度为 0 的点都可以作为起点。

3. 如何进行拓扑排序

• 一个有向图，如果图中有入度为 0 的点，就把这个点删掉，同时也删掉这个点所连的边。
• 一直进行上面处理，如果所有点都能被删掉，则这个图可以进行拓扑排序。
• 一个拓扑序列可以有多种输出方式。
• 举例说明：

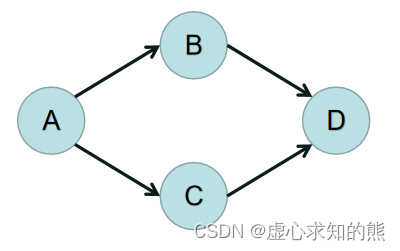
• 开始时，图是这样的状态，发现 A 的入度为 0，所以删除 A 和 A 上所连的边，结果如下图：

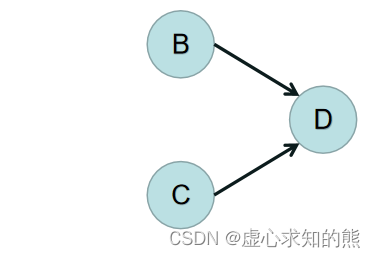
• 这时发现 B 的入度为 0，C 的入度为 0，所以删除 B 和 B 上所连的边、 C 和 C 上所连的边，结果如下图：

• 这时发现 D 的入度为 0，所以删除 D 和 D 上所连的边(如果有就删)，结果如下图：

• 这时整个图被删除干净，所有能进行拓扑排序。
• 对上述过程的实现，可以通过 queue 队列实现，入队的点的顺序就是拓扑序列。

4. 拓扑排序具体实现详见例题有向图的拓扑序列

二、有向图的拓扑序列例题——有向图的拓扑序列

题目描述

给定一个 n 个点 m 条边的有向图，点的编号是 1 到 n，图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列，如果拓扑序列不存在，则输出 −1。
若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑序列。

输入格式

第一行包含两个整数 n 和 m。
接下来 m 行，每行包含两个整数 x 和 y，表示存在一条从点 x 到点 y 的有向边 (x,y)。

输出格式

共一行，如果存在拓扑序列，则输出任意一个合法的拓扑序列即可。
否则输出 −1。

数据范围

1 ≤ n,m ≤ 1e5

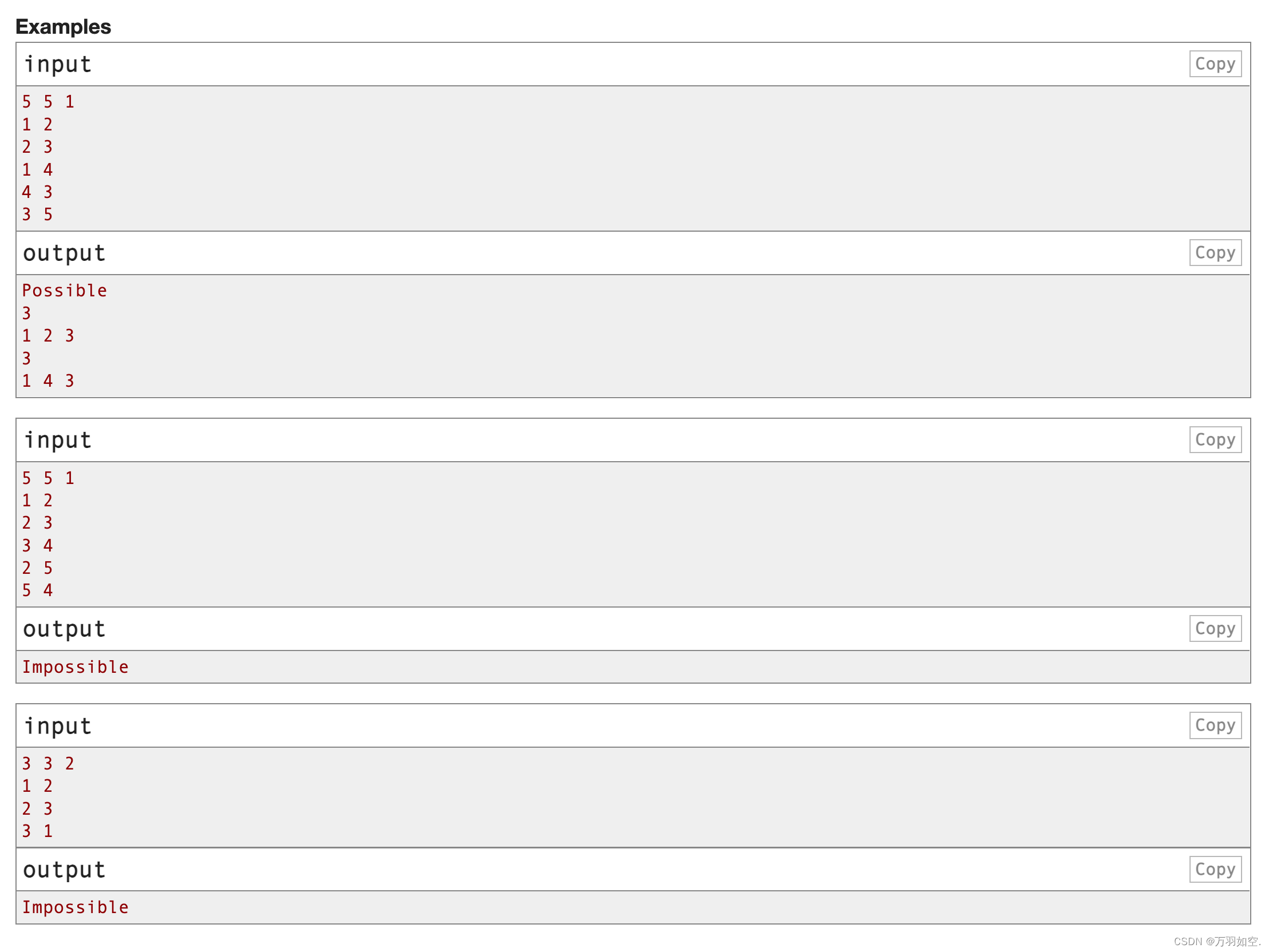
输入样例

3 3
1 2
2 3
1 3

输出样例

1 2 3

具体实现

1. 样例演示

• 输入 n=3 和 m=3 。表示一个有 3 个点，3 条边。
• 从 1 指向 2 。
• 从 2 指向 3 。
• 从 1 指向 3 。
• 如下图所示。
  

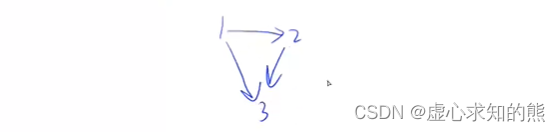
2. 实现思路

• 首先记录各个点的入度。
• 然后将入度为 0 的点放入队列。
• 将队列里的点依次出队列，然后找出所有出队列这个点发出的边，删除边，同时边的另一侧的点的入度 -1。
• 如果所有点都进过队列，则可以拓扑排序，输出所有顶点。否则输出 -1，代表不可以进行拓扑排序。

3. 代码注解

• int h[N], e[N], ne[N], idx；表示邻接表的存储方式。
• int d[N]；表示点的入度。
• int q[N]；表示队列。
• if(d[j]==0)；如果点 j 的入度为零了，就将点 j 入队。
• return tt==n-1；表示如果 n 个点都入队了话，那么该图为拓扑图，返回 true ，否则返回 false 。
• 其他注解在实现代码当中体现。

4. 实现代码

#include <bits/stdc++.h>
using namespace std;

const int N = 100010;

int n, m;
int h[N], e[N], ne[N], idx;  
int d[N];
int q[N];

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    idx ++;
}

//返回布尔序列是否存在， 若存在，则存储在q数组中
bool topsort()
{
    int hh = 0;
    int tt = -1;

    //遍历每一个节点, 入度为零则入队
    for (int i = 1; i <= n; i ++ )
    {
        if (!d[i])
        {
            tt ++;
            q[tt] = i;
        }
    }

    while (hh <= tt)
    {
        //队列不空，则取出头节点
        int t = q[hh];
        hh ++;

        //遍历头节点的每一个出边
        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (-- d[j] == 0)
            {
                tt ++; 
                q[tt] = j;
            }
        }
    }

    return tt == n - 1;
}

int main()
{
    cin >> n >> m;
    
    memset(h, -1, sizeof h);

    for (int i = 0; i < m; i ++ )
    {
        int a, b;
        cin >> a >> b;
        add(a, b);

        d[b] ++ ;
    }

    if (!topsort()) 
    {
        puts("-1");
    }
    else
    {
        for (int i = 0; i < n; i ++ )
        {
           cout << q[i] << " ";
        }
        puts("");
    }
    system("pause");
    return 0;
}