数据结构–顺序表的基本操作–插入

顺序表的插入操作

实现目标

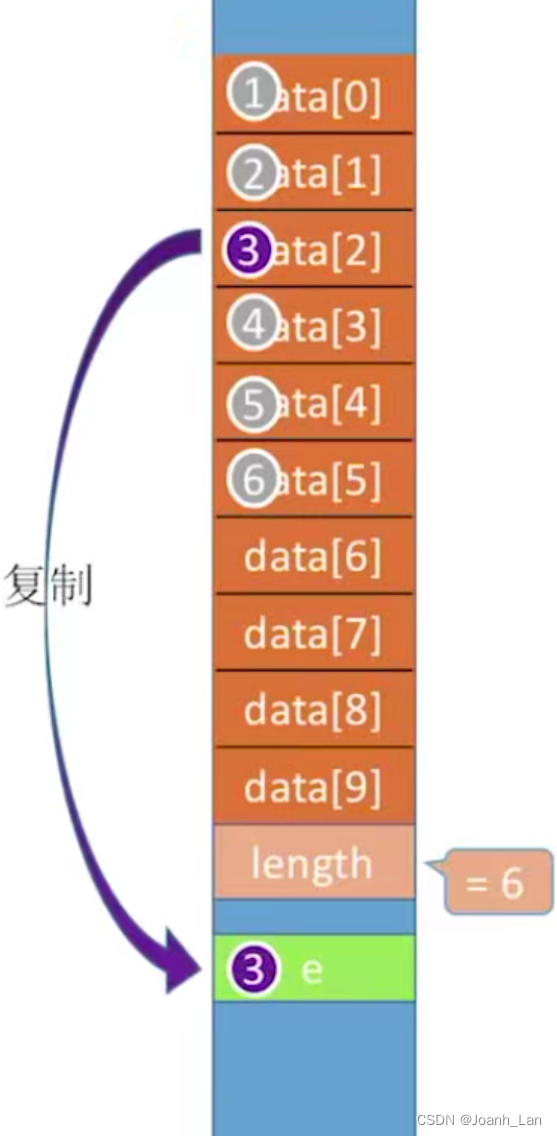
ListInsert(&L,i,e):插入操作。在表L中的第i个位置上插入指定元素e。

typedef struct
{
    int data[MaxSize];
    int len;
}Sqlist;

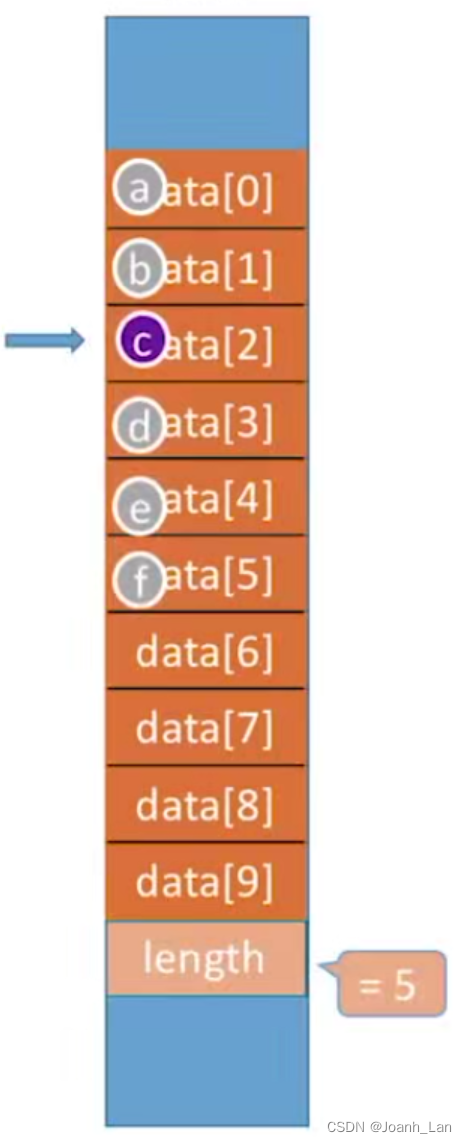
代码实现：

#include <stdio.h>
#include <stdlib.h>
#define MaxSize 10 //定于的最大长度

typedef struct
{
    int data[MaxSize];
    int len;
}Sqlist;
void InitList(Sqlist &L)
{
    L.len = 0;
}
bool ListInsert(Sqlist &L, int idx, int e)
{
    if (idx > L.len + 1 || idx < 1) //判断是否合法
        return false;
    if (L.len >= MaxSize)
        return false;

    for (int j = L.len; j >= idx; j--) //将第idx个元素及之后的元素后移
        L.data[j] = L.data[j - 1];  
    L.data[idx - 1] = e;    //在位置i处放入e
    L.len++;    //长度加1
    return true;
}
int main()
{
    Sqlist L;
    InitList(L);
    if (ListInsert(L, 1, 1))
        printf("Inserted successfully\n");
    if (ListInsert(L, 2, 2))
        printf("Inserted successfully\n");
    // 测试结果
    for (int i = 0; i < L.len; i++)
        printf("%d ", L.data[i]);
}

ps:
好的算法,应该具有“健壮性”能处理异常情况，并给使用者反馈。

时间复杂度

最好情况:新元素插入到表尾，不需要移动元素 idx = n+1，循环0次;
$最好时间复杂度$=O(1)
最坏情况:新元素插入到表头，需要将原有的n个元素全都向后移动 idx= 1，循环n次;
$最坏时间复杂度$= O(n);
平均情况:假设新元素插入到任何一个位置的概率相同，即idx= 1,2,3, … len+1的概率都是 $p=\frac{1}{n+1}$ idx = 1，循环n次;idx=2时，循环n-1次; idx=3，循环n-2次…idx=n+1时，循环0次
平均循环次数 = $np+(n-1)p+(n-2)p+...+1p=\frac{n(n+1)}{2}\times \frac{1}{n+1}=\frac{n}{2}$
$平均时间复杂度$ = O(n)

顺序表的删除操作

实现目标

ListDelete(&L,i,&e):删除操作。删除表L中第i个位置的元素，并用e返回删除元素的值。

代码实现

#include <stdio.h>
#include <stdlib.h>
#define MaxSize 10 //定于的最大长度

typedef struct
{
    int data[MaxSize];
    int len;
}Sqlist;
void InitList(Sqlist &L)
{
    L.len = 0;
}
bool ListInsert(Sqlist &L, int idx, int e)
{
    if (idx > L.len + 1 || idx < 1) //判断是否合法
        return false;
    if (L.len >= MaxSize)
        return false;

    for (int j = L.len; j >= idx; j--) //将第idx个元素及之后的元素后移
        L.data[j] = L.data[j - 1];  
    L.data[idx - 1] = e;    //在位置i处放入e
    L.len++;    //长度加1
    return true;
}
bool ListDelete(Sqlist &L, int idx, int &e)
{
    if (idx > L.len && idx < 1) //判断i的范围是否有效
        return false;
    e = L.data[idx - 1];    //将被删除的元素赋值给e
    for (int j = idx - 1; j < L.len; j++)   //将第i个位置后的元素前移
        L.data[j] = L.data[j + 1];
    L.len--;    //线性表长度减1
    return true;
}
int main()
{
    Sqlist L;
    InitList(L);
    if (ListInsert(L, 1, 1))
        printf("Inserted successfully\n");
    if (ListInsert(L, 2, 2))
        printf("Inserted successfully\n");
    int e = -1;
    if (ListDelete(L,1,e))
        printf("Deleted successfully\n");
    // 测试结果
    for (int i = 0; i < L.len; i++)
        printf("%d ", L.data[i]);
}

时间复杂度

最好情况:删除表尾元素，不需要移动其他元素 idx= n 循环0次;
$最好时间复杂度$=O(1)
最坏情况:删除表头元素，需要将后续的n-1个元素全都向前移动 idx= 1，循环 n-1 次;
$最坏时间复杂度$= O(n);
平均情况:假设删除任何一个元素的概率相同，即 idx= 1,2,3. … , len的概率都是 $p=\frac{1}{n}$
idx = 1，循环 n-1 次; idx=2 时，循环n-2次; idx=3，循环n-3 次… idx = n 时，循环 0 次
平均循环次数 = $(n-1)p+(n-2)p+......+1p=\frac{n(n-1)}{2}\times \frac{1}{n}=\frac{n-1}{2}$
$平均时间复杂度$ = O(n)

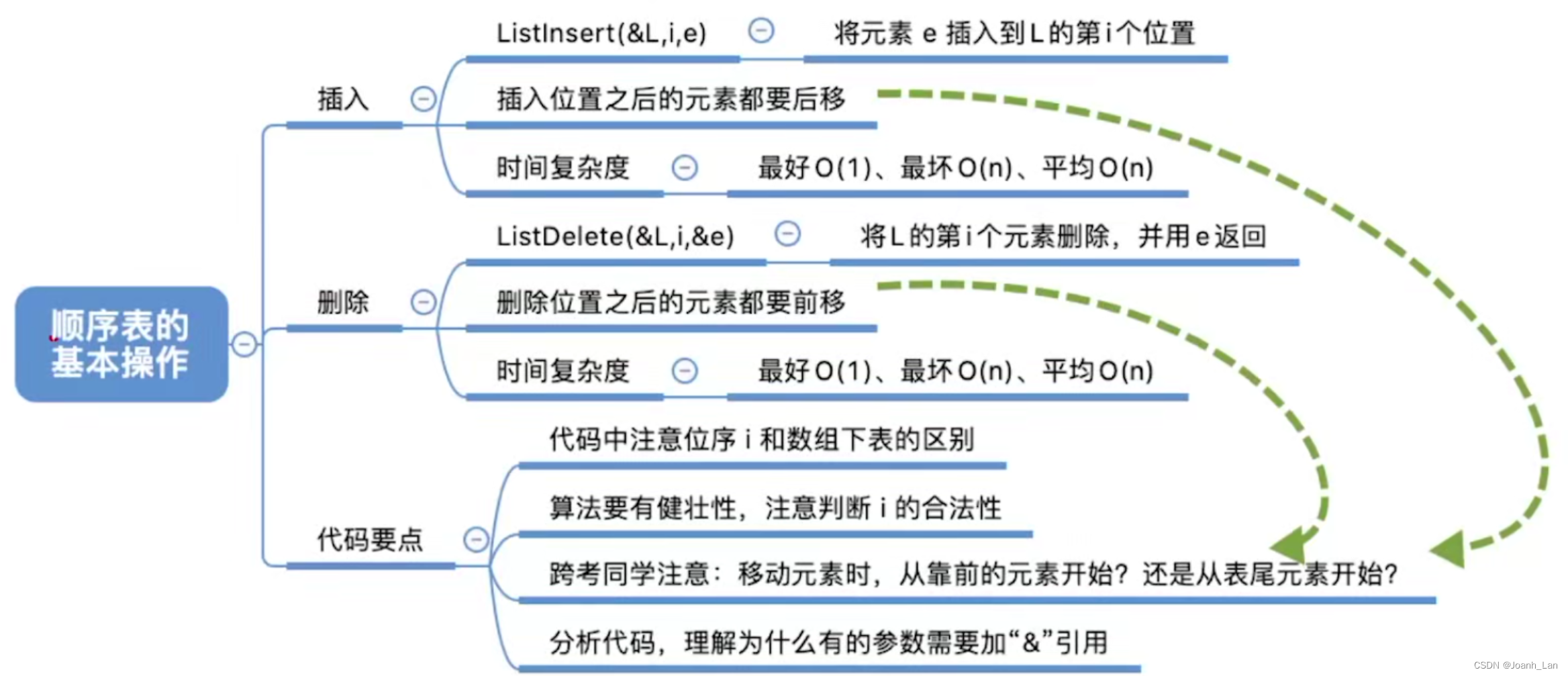
知识点回顾与重要考点