机器学习5：基于线性回归理解减少“损失”的方法

在上节《机器学习4：基本术语》中，笔者介绍了“损失（Loss）”的定义，在训练模型时，减少损失（Reducing Loss）是极为关键的，只有“损失”足够小的机器学习系统才有实用价值。

在本节中，笔者将基于线性回归（Linear Regression）来介绍减少损失的具体方法。

1.线性回归案例

2.减少损失：迭代法（An Iterative Approach）

3.减少损失：梯地下降（Gradient Descent）

4.减少损失：学习率（Learning Rate）

5.减少损失：优化学习率（Optimizing Learning Rate）

6.减少损失：随机梯度下降（Stochastic Gradient Descent）

7.参考文献

1.线性回归案例

蟋蟀（一种昆虫）在炎热的日子里会比在凉爽的日子里更频繁地鸣叫。几十年来，专业和业余科学家对蟋蟀每分钟鸣叫次数和温度的数据进行了统计，得到了一些数据，如图 1 所示。我们将这些数据绘制成图，可以方便寻找规律。

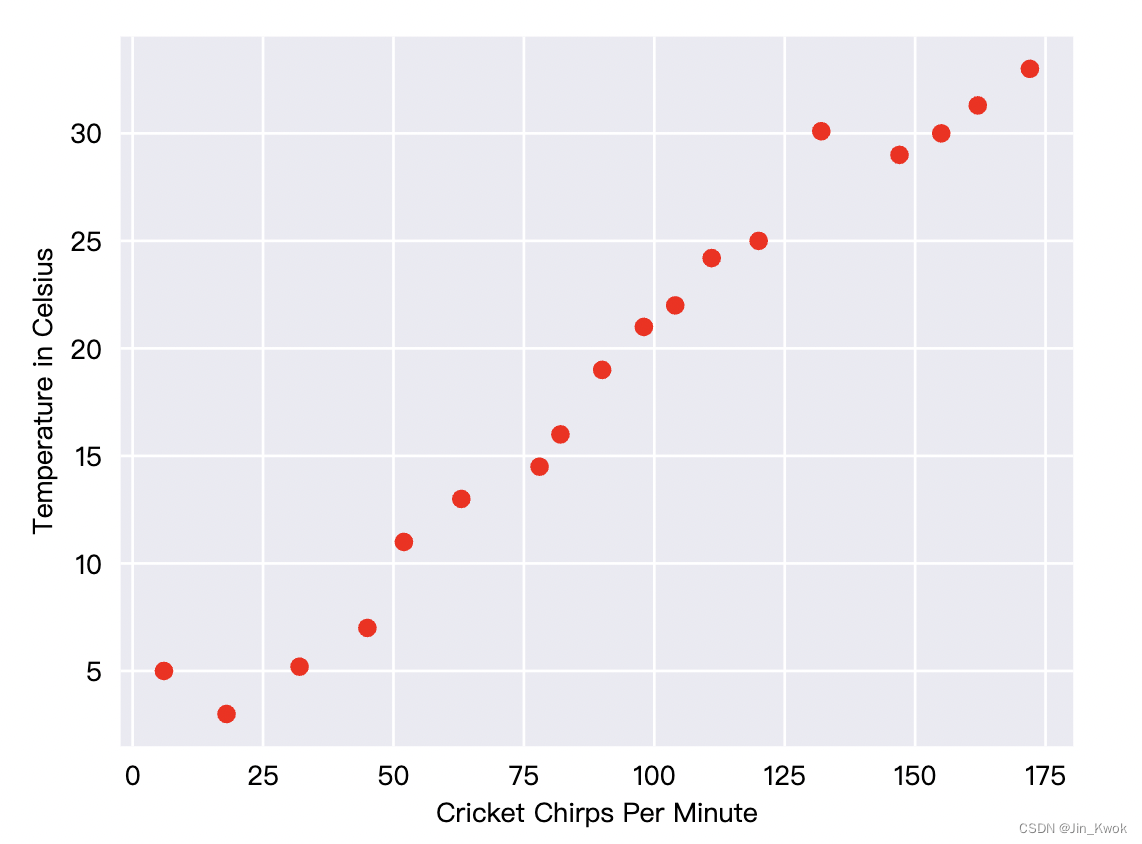
图 1 蟋蟀每分钟鸣叫声与摄氏温度的关系

很明显，图 1 显示，温度随着鸣叫次数的增加而上升。鸣叫次数和温度之间的关系是线性的吗？是的，我们可以画一条如图 2 所示的直线来近似这种关系：

图 2 线性关系

诚然，这条线并没有穿过每个点，但这条线确实清楚地显示了鸣叫次数和温度之间的关系。使用直线方程，可以将这种关系表示为：

$y=mx+b$

其中

$y$ 是以摄氏度为单位的温度——即我们试图预测的值。
$m$ 是直线的斜率。
$x$ 是每分钟的鸣叫次数——我们输入特征的值。
$b$ 是 $y$ 轴截距。

按照机器学习的惯例，我们将上述数学公式进一步形式化，从而编写如下模型方程：

$y'^{^{}}=b+w_{1}x_{1}$

在哪里：

$y^{'}$ 是预测的标签（期望的输出）。
$b$ 是偏差（ $y$ 轴截距），有时称为 $w_{0}$ 。
$w_{1}$ 是特征1（ $x_{1}$ ）的权重。权重与传统的直线方程中的“斜率”（ $m$ ）是同一概念。
$x_{1}$ 是一个特征（已知输入）。

当我们需要推断（预测）温度 $y^{'}$ 时，只需要获得蟋蟀每分钟鸣叫数值 $x_{1}$ ，并将 $x_{1}$ 的值到这个模型中，我们就可以计算出预测温度。

上述模型仅使用了一个特征，但在实际应用中，复杂的模型可能依赖于多个特征，每个特征都有单独的权重（如 $w_{1}, w_{2} ,w_{3},...$ 。）。例如，依赖三个特征的模型可能如下所示：

$y^{'} = b+w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}$

2.减少损失：迭代法（An Iterative Approach）

在上面的线性回归案例（ $y'^{^{}}=b+w_{1}x_{1}$ ）中，我们如何才能训练出模型呢？关键在于确定参数（ $b,w_{1}$ ）。通常我们很难直接确定最佳参数，而是需要不断尝试。

在寻找最佳参数的过程中，我们可以从一个疯狂的猜测开始（假设 $w_{1}$ 为 0），然后根据损失计算函数计算出损失。之后，我们可以尝试另一个猜测（假设 $w_{1}$ 为 0.5），然后再计算损失。如此往复，直到寻找出最佳参数。如图 3 所示，为机器学习算法用于训练模型的迭代试错过程：

图 3 训练模型的迭代方法

在实际应用中，“模型” 可能采用一个或多个特征作为输入并返回一个预测（ $y^{'}$ ）作为输出。为了简化，这里考虑采用一个特征并返回一个预测的模型：

$y'^{^{}}=b+w_{1}x_{1}$

上述模型中，我们应该为 $b$ 和 $w_{1}$ 设置什么初始值？对于线性回归问题，事实证明初始值并不重要。我们可以选择随机值，但我们只会采用以下简单值：

$b=0$
$w_{1}=0$

假设第一个特征值为 10。将该特征值代入预测函数会得到：

$0=0+0\ast 10$

图中的 “计算损失” 部分是模型将使用的损失函数。假设我们使用平方损失函数（MSE）。损失函数接受两个输入值：

$y^{'}$ ：模型基于特征 $x$ 作出的预测
$y$ ：特征 $x$ 对应的正确标签

之后，如图 3 所示，通过 “计算参数更新（compute parameter updates）” ，机器学习系统检查损失函数的值并生成新的值 $b$ 和 $w_{1}$ 。基于新的值，机器学习系统继续迭代，直到发现损失尽可能最低的模型参数。通常，随着迭代的进行，总体损失会停止变化或变化极其缓慢，当这种情况发生时，我们说模型已经收敛。

3.减少损失：梯地下降（Gradient Descent）

在迭代法一节中，计算参数更新（compute parameter updates）模块（图 3 所示）到底如何实现呢？我们并没有展开介绍，本节将介绍一种实用的参数更新方法——即梯度下降法。

假设我们有足够的时间和计算资源来尝试所有可能的 $w_{1}$ 值并计算损失。对于回归问题，我们可以得到 $w_{1}$ 与损失的关系图，如图 4 所示。

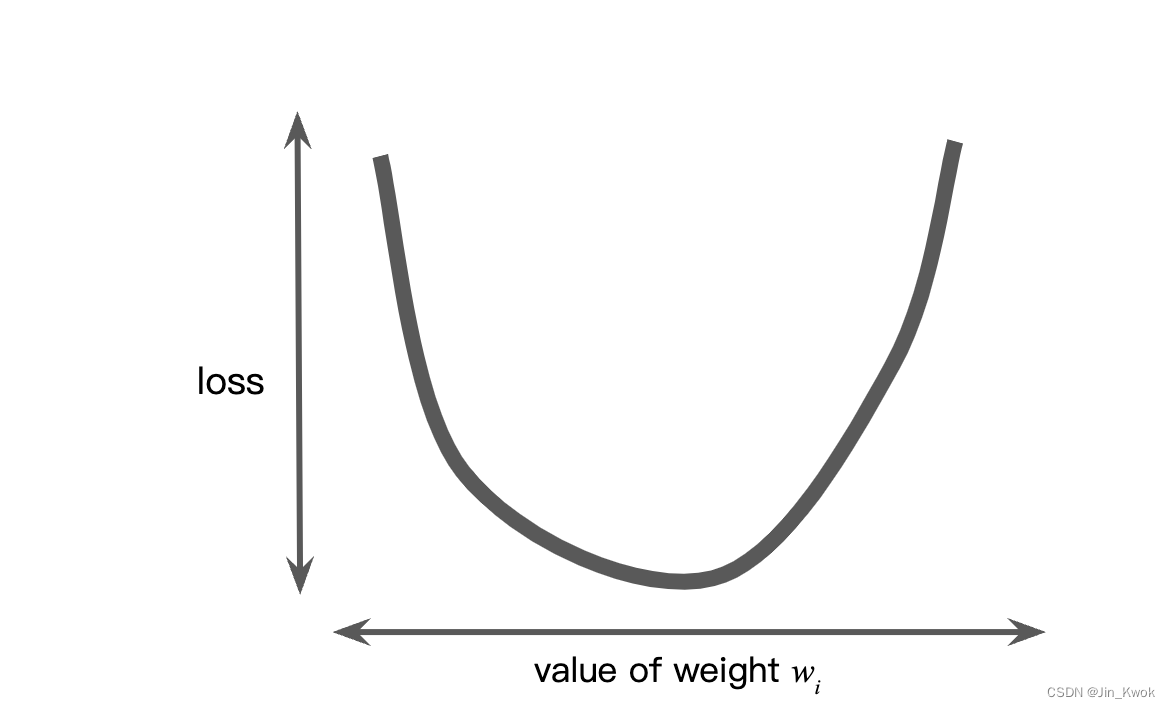
图 4 回归问题产生损失与权重关系图

图 4 所示本质上是一个凸问题（在欧氏空间中，对于集合中的任意两个点，连接它们的直线上的每个点也在该集合内，自行百度，不展开解读）。凸问题只有一个最小值，也就是说，只有一个地方斜率恰好为 0。该最小值是损失函数收敛的地方。

计算每个可能的 $w_{1}$ 值的损失函数值，从而在整个数据集上寻找收敛点。在实践中，我们可以采用一种高效的机制（在机器学习中非常流行），即梯度下降。

梯度下降的第一阶段是选择一个起始值（起点） $w_{1}$ 。出发点并不重要，重要的是更新方法。因此，很多算法只是简单地将 $w_{1}$ 设置为 0 或选择一个随机值。如图 5 所示，选择了一个略大于 0 的起点。

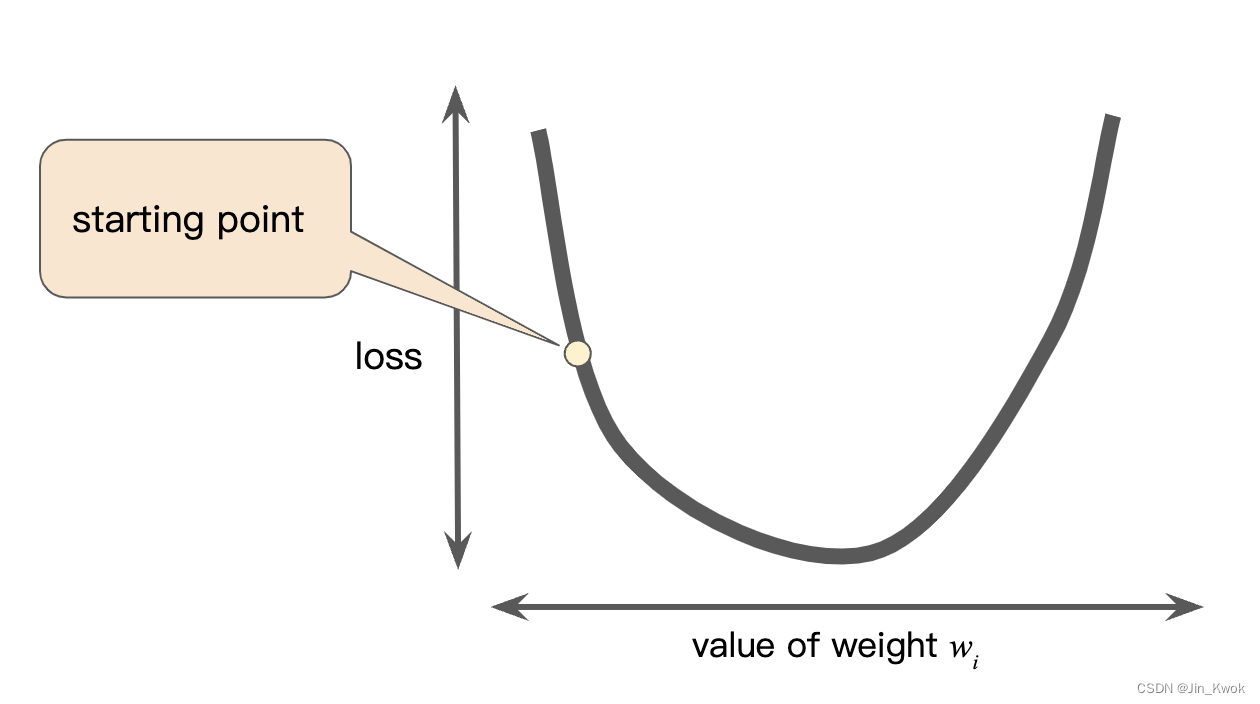
图 5 梯度下降的起点

然后，根据梯度下降算法计算损失曲线在起始点的梯度。在图 5 中，损失的梯度 = 曲线的斜率（导数），当存在多个权重时，梯度是关于权重的偏导数的向量。需要注意的是，梯度是一个向量，因此它具有以下两个特征：

一个方向
一个量级

梯度总是指向损失函数增长最快的方向。如图 6 所示，梯度下降算法向负梯度方向迈出一步，以尽快减少损失。

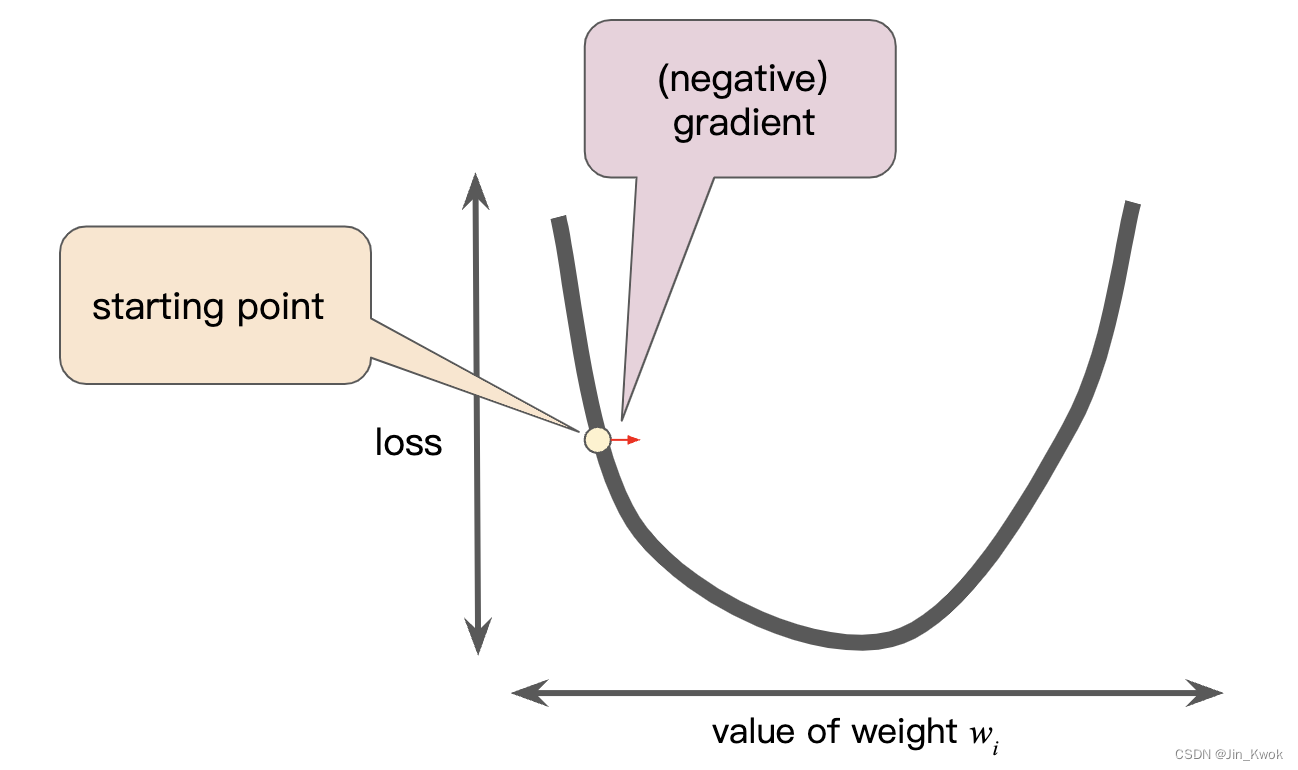
图 6 梯度下降依赖于负梯度

为了确定损失函数曲线上的下一个点，梯度下降算法将梯度大小的一部分添加到起点，如下图所示：

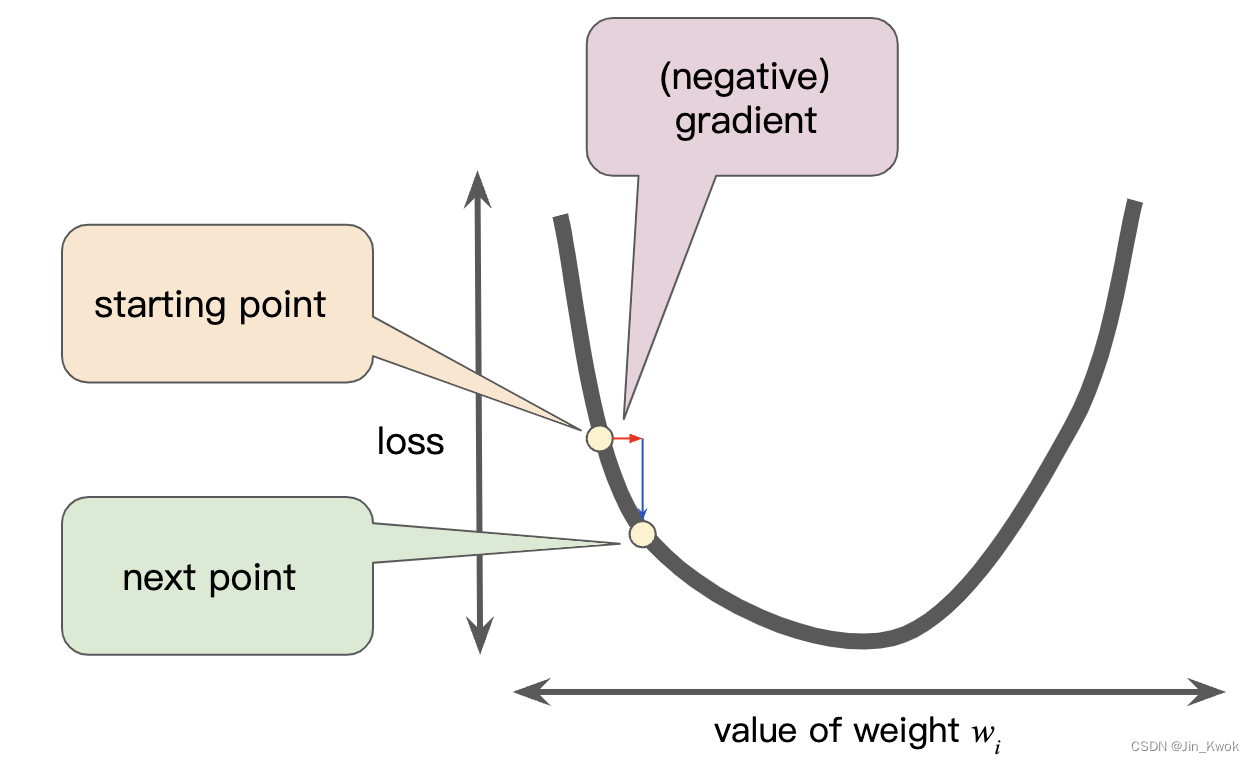
图 7 通过“梯度”可移动到损失曲线上的下一个点

然后梯度下降重复这个过程，逐渐接近最小值。

4.减少损失：学习率（Learning Rate）

如前所述，梯度向量具有方向和大小。梯度下降算法将梯度乘以一个被称为学习率（有时也称为步长-step size）的标量来确定下一个点。例如，如果梯度幅度为 2.5，学习率为 0.01，则梯度下降算法将选择距离前一个点 0.025 的下一个点。

超参数是工程师在机器学习算法中调整的旋钮。大多数机器学习工程师将花费大量时间来调整学习率。如果选择的学习率太小，学习花费的时间将会非常长，如图 8 所示。

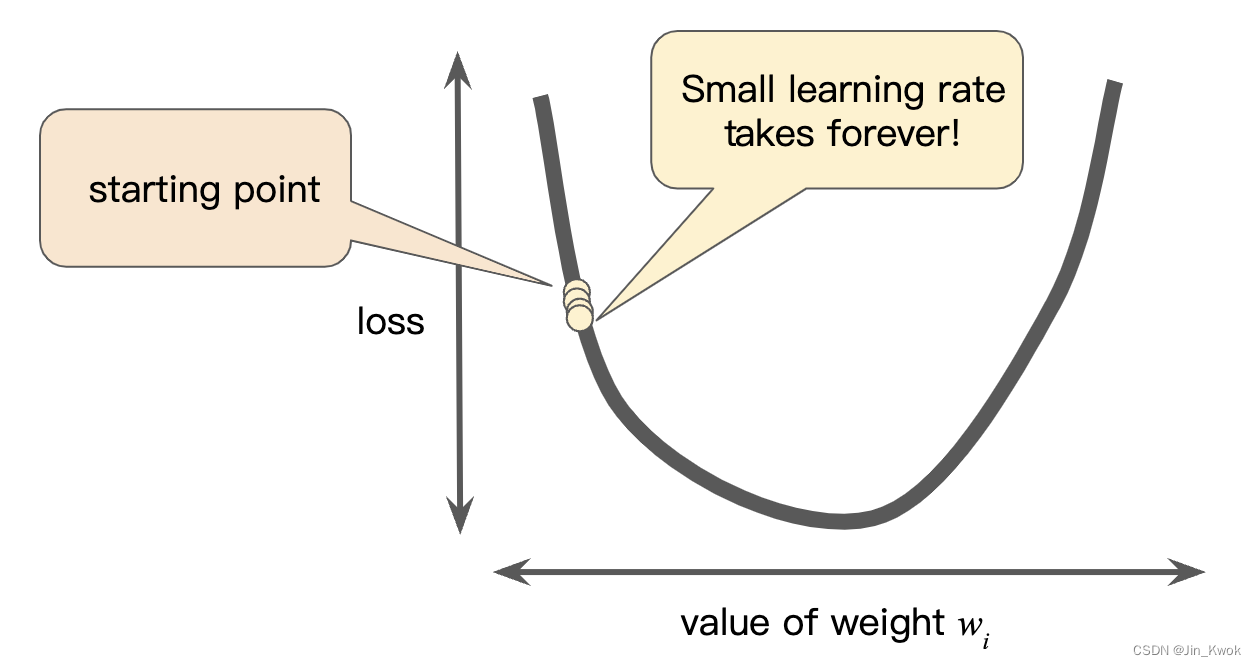
图 8 学习率太小

相反，如果指定的学习率太大，下一个点将永远在井底随意摆动，就像量子力学实验出了严重的错误，如图 9 所示，可能无法找到最优的点。

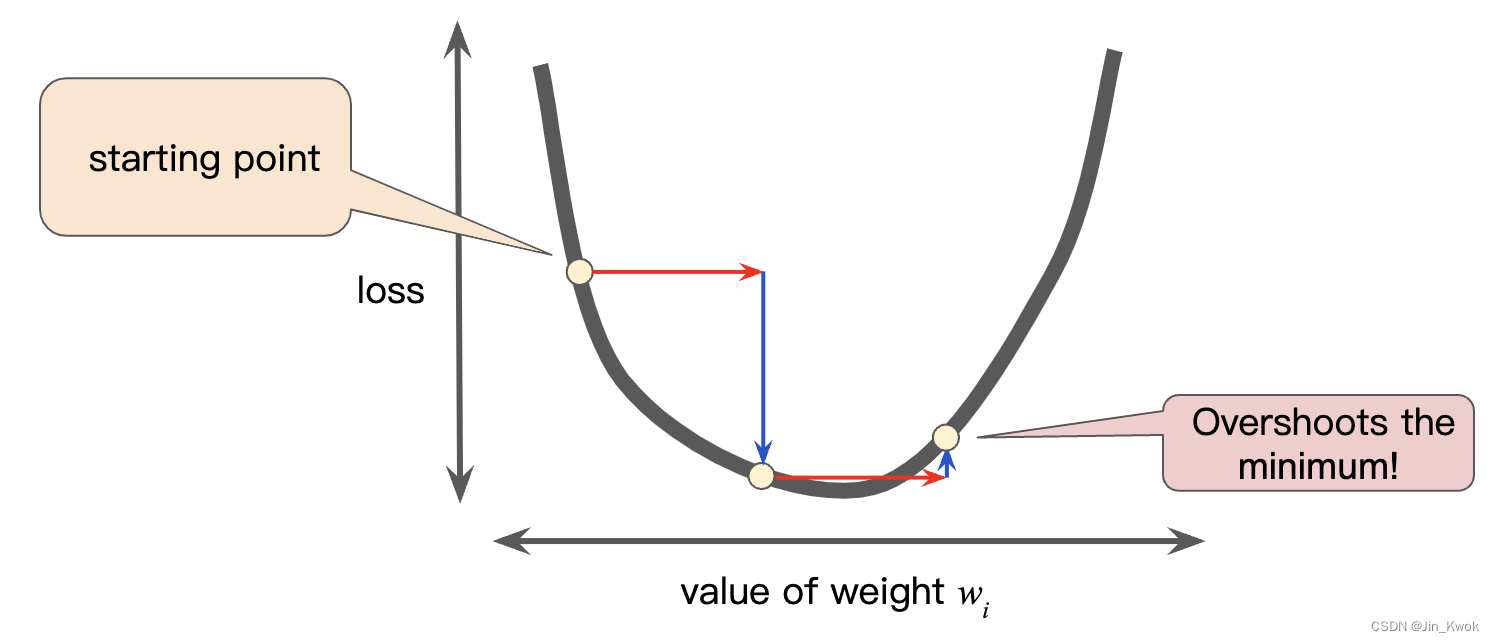
图 9 学习率太大

每个回归问题都有一个金发姑娘学习率（即最佳学习率）。最佳学习率与损失函数的平坦程度有关。如果你知道损失函数的梯度很小（函数曲线很“平坦”），那么就可以安全地尝试更大的学习率，这可以补偿小梯度并产生更大的步长。反之，如果损失函数的梯度很大（函数曲线很“陡峭”），那么应采用较小的学习率。

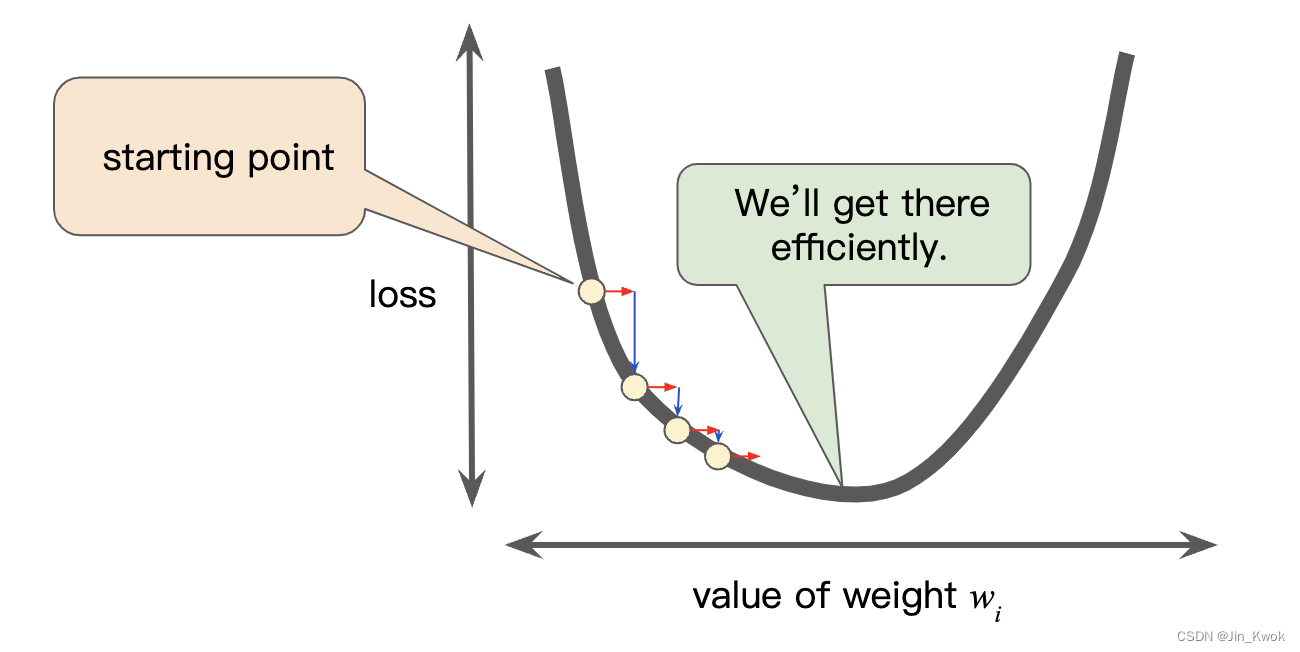
图 8 学习率恰到好处

5.减少损失：优化学习率（Optimizing Learning Rate）

本节，我们通过一个例子来尝试不同的学习速率，看看它们如何影响达到损失曲线最小值所需的步数。如图 9 所示

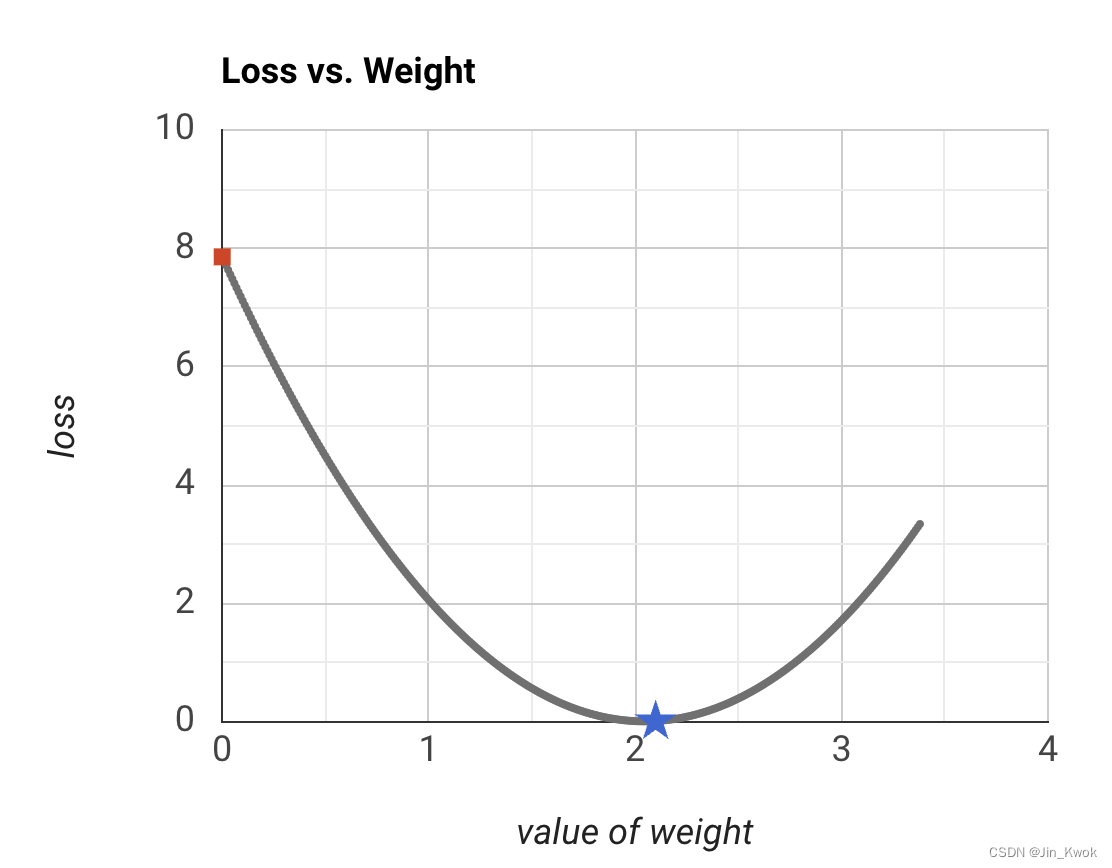
图 9 学习率案例

若设置学习率为 0.03，经过 40 步，梯度下降算法达到损失曲线的最低点。若设置学习率为 0.1，经过 11 步，梯度下降算法达到损失曲线的最低点（如图 10 所示）。若设置学习率为 1，梯度下降永远不会达到最小值。通过尝试，我们发现：该损失函数的最佳学习率介于 0.2 到 0.3 之间，三到四步后就会达到最小值。

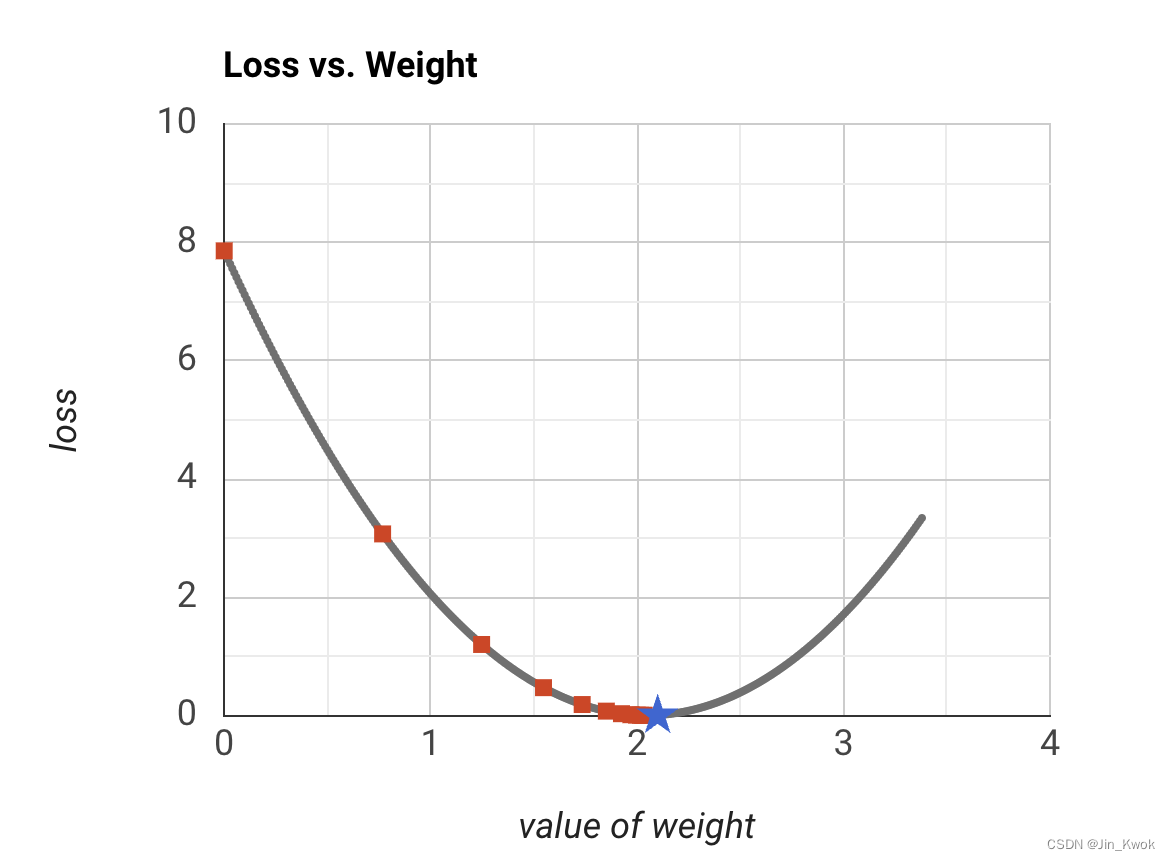
图 10 学习率=0.1

在实践中，找到“完美”（或接近完美）的学习率对于成功的模型训练并不重要。目标是找到一个足够大的学习率，使梯度下降有效收敛，但又不能大到永远不会收敛。

6.减少损失：随机梯度下降（Stochastic Gradient Descent）

在梯度下降中，批次是在单次迭代中用于计算梯度的示例总数。到目前为止，我们假设该批次是整个数据集。然而，在实际应用中，数据集通常包含数十亿甚至数千亿的示例，同时，数据集通常包含大量特征。因此，批量可能会很大。非常大的批次甚至可能导致单次迭代需要很长时间来计算，而这几乎是不可行的。

对大型数据集进行随机采样得到结果中可能包含冗余数据。事实上，随着批量大小的增加，冗余变得更有可能。虽然一些冗余对于消除噪声很有用，但过于巨大的批量也是不合适的。

在实践中，以更少的计算量来获得正确的梯度是我们所追求的。通过从数据集中随机选择示例，我们可以从较小的平均值中估计出较大的平均值（尽管是嘈杂的）。 随机梯度下降( SGD ) 将这一想法发挥到了极致——每次迭代仅使用一个示例（批量大小为 1）。如果有足够的迭代次数，SGD 可以工作，但噪音很大。术语 “随机” 表示随机选择包含每一批次的一个示例。

小批量随机梯度下降（小批量 SGD）是全批量迭代和 SGD 之间的折衷方案。小批量通常包含 10 到 1,000 个示例，是随机选择的。小批量 SGD 减少了 SGD 中的噪声量，但仍然比全批量更有效。