扯淡:
今天期末复习的时候发现一个算法很有意思,就是男女最大分配对象问题,几对男女最多能凑够几对对象。
根据社会主义核心价值观,我们最好整一夫一妻制,分配一人一对象,我辈义不容辞。
题目分析:
这题有一说一,网上的分析是匈牙利算法,我就此打住不谈,因为我。。也不太理解。要想深刻理解,请移步匈牙利算法的系统学习。
结合网友的分析,我对这道男女分配问题给出我自己的理解。
题目是尽可能多的给男女匹配,说通俗的话就是这么撮合,才能凑合最多的情侣。
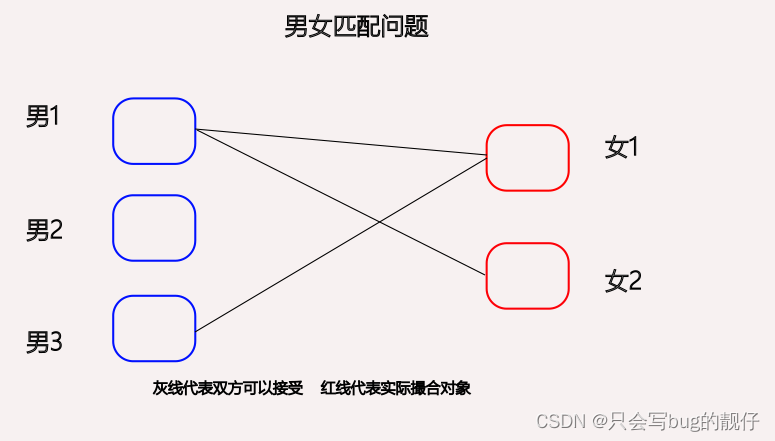
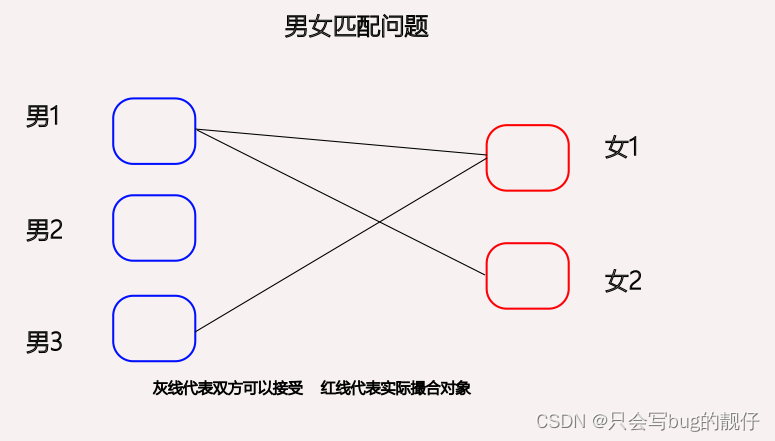
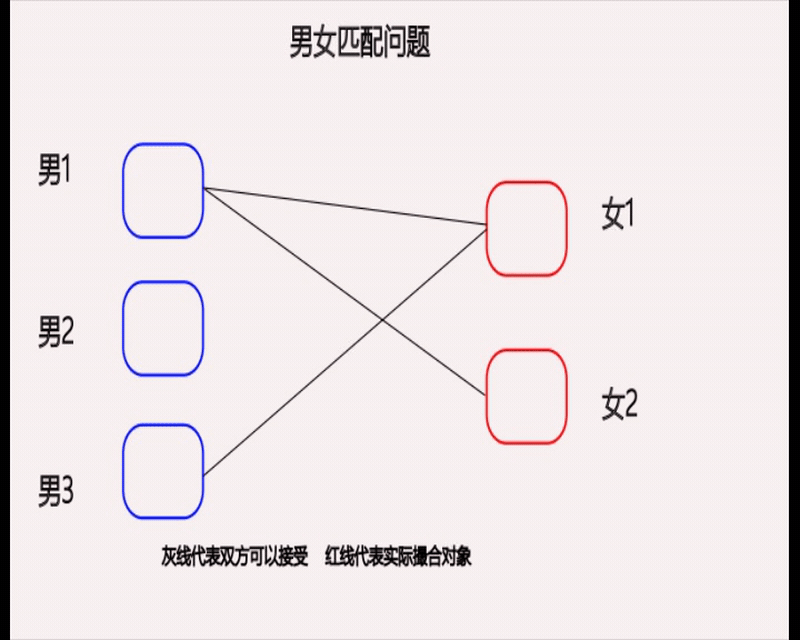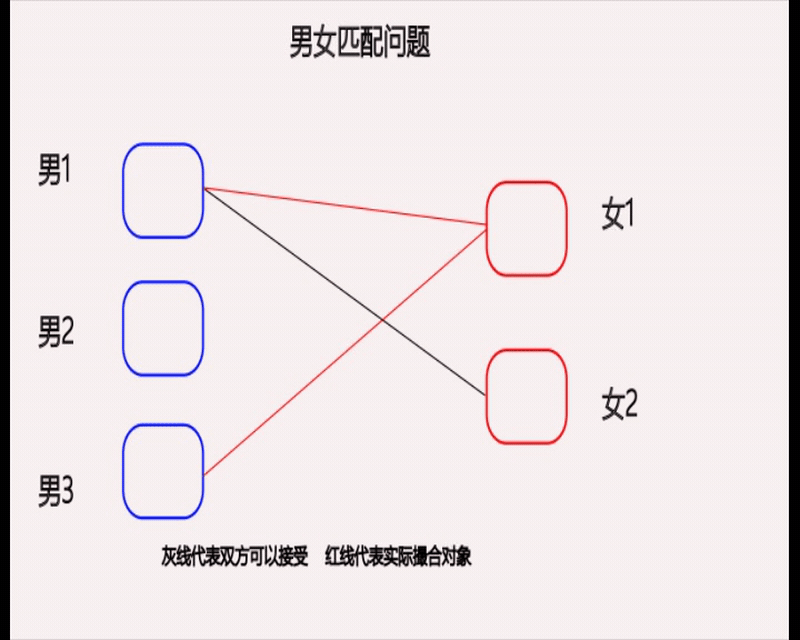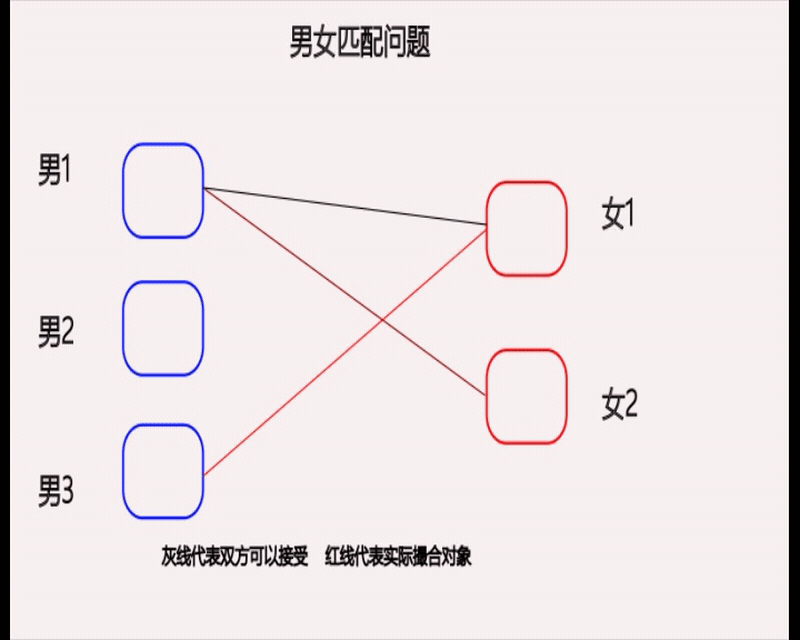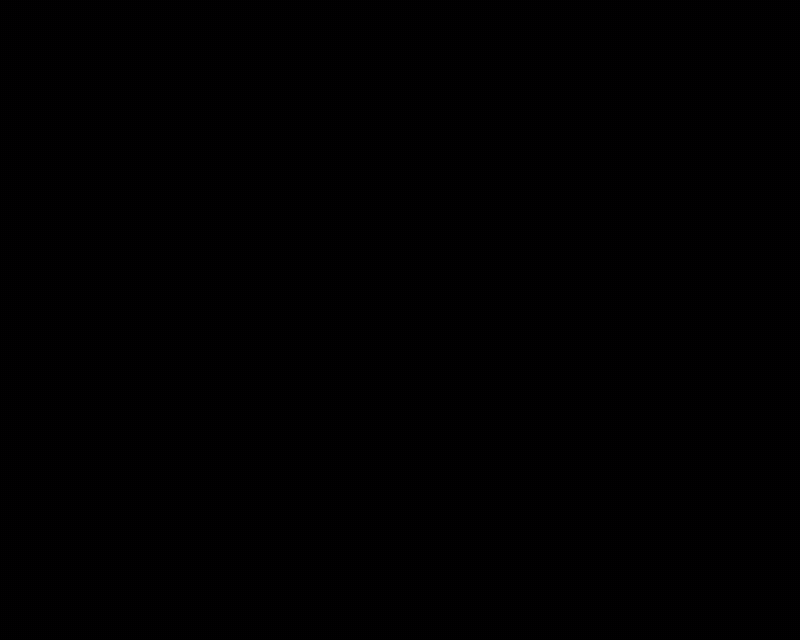
以该图为例,男1和女1和女2互相喜欢,男3又喜欢女1。
最好的撮合结果就是让男1和女2结合,男3和女1结合。这样可以组成两对,如果女1和女1进行结合的话只能凑合成1对
我们在撮合的过程中,有备胎的尽量给没备胎的让对象。这样就人人开心,独乐乐不如众乐乐。
我们可以这样进行解决:
- 从男1开始,轮流给男生找对象。
- 如果某个男生喜欢的对象已经配对完成的话,那么可以让那个配对的男同胞找一找有没有备胎,如果有的话,让已经配对的对象找备胎,把这个对象让给我。
emm,可能听起来有点绕,我就用上面的动图进行演示一下吧。
下面是宁大的一道相关题。
某大学组织 n 个学生去多家单位实习,如果所有单位总共可以提供 m 个实习岗位,实习生和实习单位经过洽谈后双方自愿进行,校方则希望能够达到实习人数最大化。假设双方彼此只有愿意和不愿意,没有优先程度考虑,试采用合适的二分图结构表示该过程,并设计合理的算法实现二分图的最大匹配,达到实习人数最大化。
和上面异曲同工。
public class MaxMatching {
private int n; // 学生数
private int m; // 实习岗位数
private boolean[][] graph; // 二分图的邻接矩阵
private int[] match; // 存储每个学生匹配的实习岗位编号
private boolean[] visited; // 存储每个学生是否已经被访问过
public MaxMatching(int n, int m, boolean[][] graph) {
this.n = n;
this.m = m;
this.graph = graph;
this.match = new int[m];
Arrays.fill(match, -1);
this.visited = new boolean[n];
}
public int getMaxMatching() {
int count = 0; // 记录匹配的学生数
for (int i = 0; i < n; i++) {
Arrays.fill(visited, false);
if (find(i)) {
count++;
}
}
return count;
}
private boolean find(int student) {
for (int i = 0; i < m; i++) {
if (graph[student][i] && !visited[i]) {
visited[i] = true;
if (match[i] == -1 || find(match[i])) {
match[i] = student;
return true;
}
}
}
return false;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
boolean[][] graph = new boolean[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
graph[i][j] = scanner.nextInt() == 1;
}
}
MaxMatching maxMatching = new MaxMatching(n, m, graph);
System.out.println(maxMatching.getMaxMatching());
}
}
结语:
漫漫算法路,太难了!呜呜呜呜!