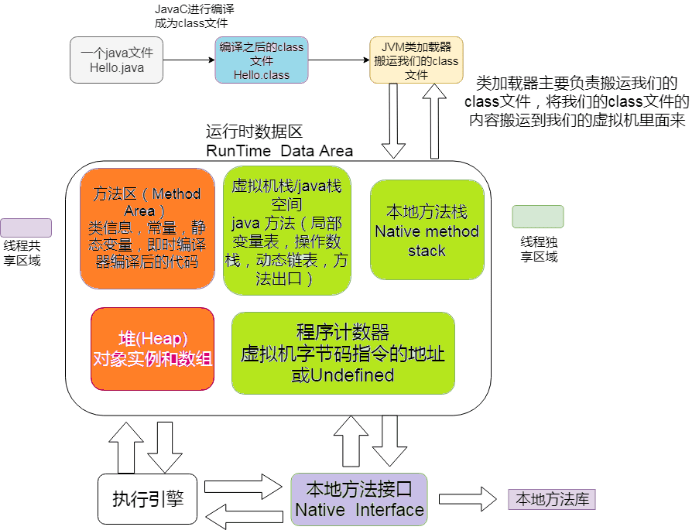
学会二叉树不知道干啥?二叉树的深度优先搜索和广度优先搜索,我要打十个乃至二十个(打开你的LeetCode撸起来)学练并举_二叉树广度优先搜索_小杰312的博客-CSDN博客

上述文章，初步介绍了搜索过程和关于二叉树中进行搜索的很多实例。将搜索的过程写的还是很详细的。很有套路性。学会可以很明了整个搜索的过程。但是对搜索算法的认知深度和层次还不够。还不够下细。很多细节之处的打磨还不够。所以今日，再次基础之上，希望可以将细节打磨的更加到位。加深自身对于搜索算法的认知。以及增强递归代码书写的可控性。

认知：

搜索算法题目 (广度, 深度, 记忆化)

搜索的本质是什么? 状态树展开遍历的过程中根据题意寻找目标结点.
搜索的过程总是从初始状态展开的过程.
从搜索过程中就形成了一棵以初始状态为根节点、包含所有可能到达目标状态的路径的状态树。

搜索的方式/策略多种多样. 但是本质正是一种遍历, 遍历的过程中排除不要的。寻求并且留下要的。

找到要的就可以开始返回。携带着题目要求信息返回.

注意1: 既然是遍历, 我们需要做到不重不漏.
注意2: 递归中传值暗含着回溯. 天然的可以回到之前的特性。但是切记, 传参时&引用可以打破这种天然的回溯 (递归的本质是深搜)
注意3: 递归调用的看待 (不要单纯看作一层函数, 而是看作一个套娃盲盒. 不知道多少层的盲盒)
注意4: 把握好递归函数的返回, 时机(返回条件) 和顺序, 位置缺一不可.

递归最难最难的是什么?

最难最难的其实不是做题. 而是不受掌控的做题.

初练递归题目的时候, 相信大家都会心生如此感受, 题目做出来了。但是感觉很模糊，
只是凭借着大量的肌肉记忆做出来了。我会做了。但是不是所有的递归题目我都有把握。
如果状态好可能就AC了，状态不好，可能就会一直卡在那里，知道大致思路，但是难以递归实现。

通过有思路, 有方向性的训练来培养对递归代码的掌控程度?

递归函数参数的设计性 (常规：当前状态, 目标状态, 引用&携带返回信息)
参数可以增加搜索的限制条件
返回值设计性：返回值也可携带返回信息.
终止条件的设计性. (返回的位置)
终止条件：success search ans and failure search ans.

从最天然的递归结构 --- 树（初步感受递归dfs(深度搜索)）

236. 二叉树的最近公共祖先

力扣

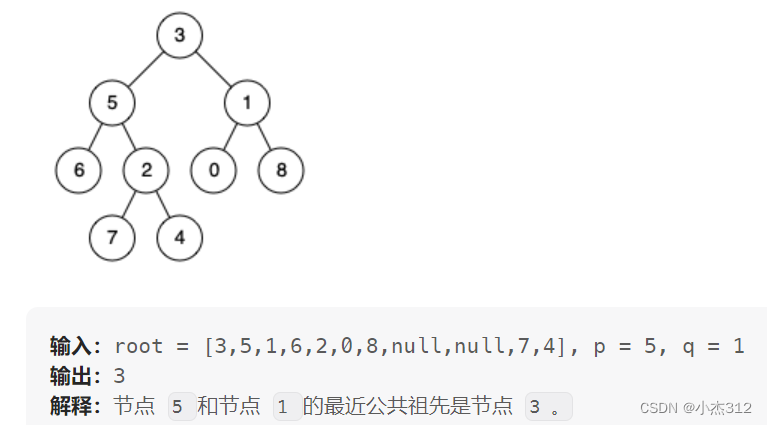
怎么做 ? 先用我们正常人是思想思考。如果我们都从下向上走。5 和 1分别向上上去之后第一个交汇点就是答案。

转换：思想很简单了。我们找到了两个目标结点之后，向上走。走到第一个交汇就是答案。

1. 怎么找到目标结点。（搜索）

2. 怎么知道已经找到目标结点。（判断。靠什么判断。回去的的时候带点东西来判断：记住。判断，没别的，如果是回溯的时候判断子树是否搜索到目标，用的就是返回值。最好用。参数虽然也可。但是麻烦。）

3. 怎么向上的. （回溯，递归回溯的时候天然的状态回退）

4. 怎么判断交汇. （左边通知上来一个目标，右路也通知上来一个目标）

5. 怎么将交汇时候的答案结点返回。（看如何设计了。究竟是全局？还是局部返回？还是参数带出？）

Coding 递归代码。最具精简，应该要非常体现每一步的可读性。简洁易懂，明了清晰。如果那一步的意图不清楚，说明这个题目的AC是运气，而非实力。

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == nullptr) return nullptr;
        // 找到q或者p 返回.
        if (root->val == p->val || root->val == q->val) return root;
        // 递归展开. 套娃深入. 并且用lchild rchild 拿到左右路回溯上来的结果
        TreeNode* lchild = lowestCommonAncestor(root->left, p, q);
        TreeNode* rchild = lowestCommonAncestor(root->right, p, q);
        //交汇点。ans所在处
        if (lchild && rchild) return root; 
        //交汇点之前和之后, 携带搜索目标和答案返回. so do this
        if (lchild || rchild) return lchild != nullptr ? lchild : rchild;
        return nullptr;//找不到
    }
};

上述代码获得了正确的答案。但是我的思路是存在问题的。是存在致命缺陷的。

我只考虑了从左右两路同时上来交汇于一处。但是我没有考虑一路上来。Waht? 什么意思？没错，就是存在一个结点即是题目要求结点本身。但是也是交汇结点的情况。

我携带着错误的思想写出的第一版错误代码：一直没有通过，卡在这里：错误代码如下：

class Solution {
    TreeNode* ans;
    bool dfs(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == nullptr) return 0;
        // 找到q或者p 返回.
        if (root->val == p->val || root->val == q->val) {
            return 1;
        }
        // 递归展开. 套娃深入. 并且用lchild rchild 拿到左右路回溯上来的结果
        bool lSearchAns = dfs(root->left, p, q);
        bool rSearchAns = dfs(root->right, p, q);
        //交汇点。ans所在处
        if (lSearchAns && rSearchAns) {
            ans = root;
            return 0;// 反正只有一组答案. 找到之后剩下的都不能是ans了.
        } 
        //将这一路的结果带回
        if (lSearchAns || rSearchAns) return 1;
        return 0;//找不到
    }

public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == nullptr) return nullptr;
        dfs(root, p, q);
        return ans;
    }
};

上述代码几乎完全就是最上面代码的翻版。但是很遗憾第二款代码是错误的。我很庆幸。写了第二版错误代码。发现了自己思维的缺陷。

其实就仅仅只是return ，还有一处return 或许是有问题的。那就是找到q或者p的返回。如果我在此处添加ans = root; 便可以如愿AC.

// 找到q或者p 返回. OR may be, return ans? what? p OR q maybe just equal ans. 哈哈哈。。。需要考虑。q 和 p本身就是交汇点。这是我初次做这个题目没有思考到的。虽然但是还是莫名其妙AC。但是这就是递归。

if (root->val == p->val || root->val == q->val) return root;

递归设计的艺术：我们需要整体的解决问题的一个格局。一个整体的流程。先从最简单的问题解决本身入手。思考需要些什么。需要的东西在那个阶段。处理的先后顺序。。。

处理逻辑（收集每一层最大值OR遍历收集特定结点...） + 处理阶段 (递归深入阶段) OR (递归回溯阶段) 回溯阶段。专门对应了一种算法。叫做回溯... 也是特别重要。特别适合路径收集.

答案收集的阶段性

力扣

124. 二叉树中的最大路径和

力扣

又是一道很经典的题目。题目很经典，难度就看看。不管难不难，我们学习算法嘛。最好深入思路。题目逻辑，细节考虑的难度。我们就慢慢积累。

分析： 路径就是连在一起的多个结点序列。然后结点不可重复。路径起点不一定是根部。然后找最大路径和。有意思。这个题目搞明白，深度优先搜索，递归过程理解，回溯阶段理解都可以更加深刻了.

这个路径，完全随意呀。只要是连着的几个结点，起点任意。不交叉重复就OK.

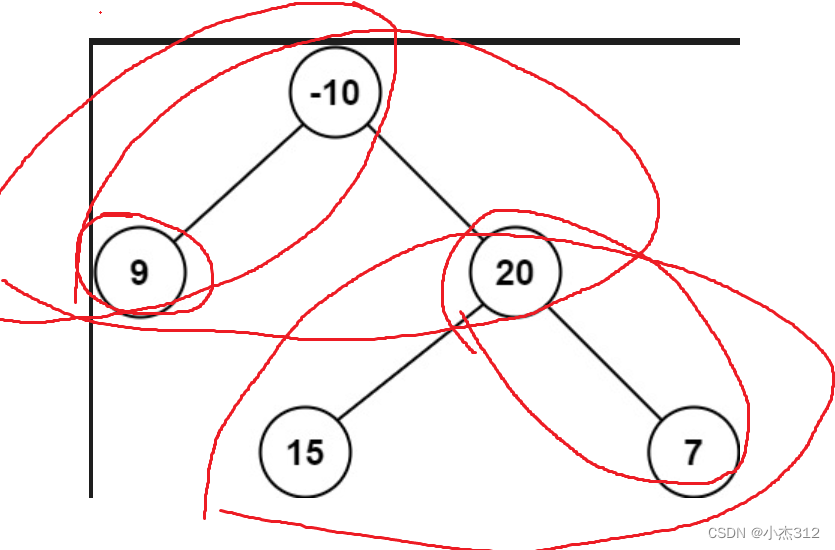
观察我画的这个图：什么意思。答案可能不一定在上边。答案可能就在下面。

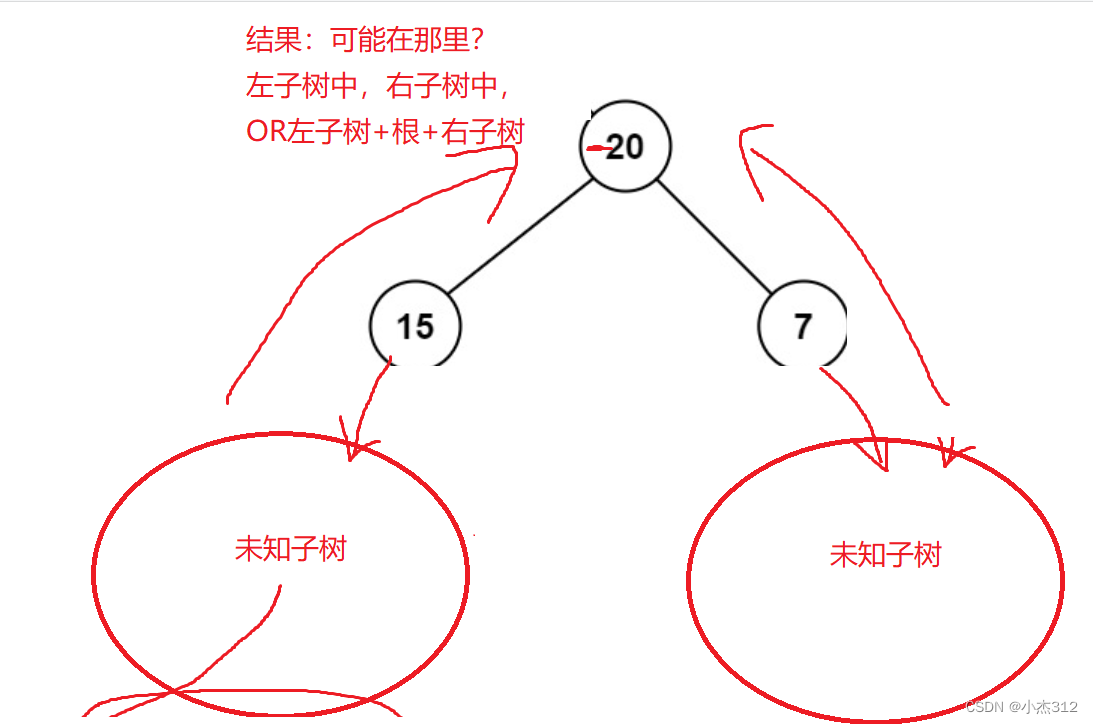
我们必须搞清楚的是：最大的路径结果，可能是左子树独立，右子树独立，又或者是左子树，根部，右子树，拼接在一起，左子树拼接根部，右子树拼接根部，均可能.

class Solution {
    int ans;    
    int dfs(TreeNode* root) {
        if (root == nullptr) return 0;
        //获取左右子树路径最大值. 可跟根部拼接的最值
        int lsum = dfs(root->left);
        int rsum = dfs(root->right);
        
        //可能的答案收集, 左子树+根部, 右子树+根部. 单独根部. 左子树+根部+右子树
        //因为选择是最优子路径, 所以左右子树不可舍弃. 绝对>0
        ans = max(ans, lsum+root->val);
        ans = max(ans, rsum+root->val);
        ans = max(ans, root->val);
        ans = max(ans, lsum+root->val+rsum);

        //选择和上面根部拼接的最优子路径
        int retval = max(lsum+root->val, rsum+root->val);
        retval = max(retval, 0);
        retval = max(retval, root->val);
        return retval;
        
    }
public:
    int maxPathSum(TreeNode* root) {
        ans = INT_MIN;
        dfs(root);
        return ans;
    }
};

此题难点在于细节多，思路思考清楚之后就是一些细节处理了。思路就是左子树，右子树，左右子树根部何在一块，都有可能产生答案.

递归参数设计性

力扣

分析题目：啥叫作堂兄弟，这是我们需要抓住的重点，证明是堂兄弟需要哪些关键信息. 深度相同，说明是同一辈的，老爹不同，说明是堂兄弟.

咋做捏？两个办法？深度相同，其实也就是同一层嘛，可以用广度搜索。广度搜索就是那种一面面，一层层，一圈圈的处理。我的感觉就是一种原点扩散。一个原点向外一圈一圈，一层一层的展开。这个就是广度嘛。因为是按照一定的距离，或者权重绕着起点扩散搜索的。所以距离是慢慢扩大的。同一层距离最开始的位置都是一个间距。我靠。说开了。这么一说。其实层序后面的理论都说完了。

不过这个题目，我还是想用深搜去做。不论别的，提高递归参数，返回值。。。设计能力。我最开始的适合说过，参数其实是用于携带条件信息的。或者做传出参数，相当于返回值。当然，此处的爹爹必须携带。不然，我们咋晓得是不是一个爹？自然深度相同，我们还需要携带回来深度。深度可以用返回值带回来。

OK. 开搞，这个自然是需要搜索两次了。非常的明显，一次搜索可能应该我是没办法实现的。此处的parent因为传入的是& 所以，每次在递归调用之前，需要我们手动进行parent的设置.

class Solution {
    int dfs(TreeNode* root, int x, TreeNode*& parent) {
        if (root == nullptr) return -1; //null深度设置为-1, 没找到
        if (root->val == x) return 0;//找到了返回
        parent = root;//设置parent
        int ldeep = dfs(root->left, x, parent);
        if (ldeep != -1) return ldeep+1;
        parent = root;//回溯, 设置parent
        int rdeep = dfs(root->right, x, parent);
        if (rdeep != -1) return rdeep+1;
        return -1;
    }

public:
    bool isCousins(TreeNode* root, int x, int y) {
        if ( root == nullptr) return false;
        TreeNode* parentx = nullptr, *parenty = nullptr;
        int deepx = dfs(root, x, parentx);
        int deepy = dfs(root, y, parenty);
        return parentx != parenty && deepx == deepy;
    }
};

int ldeep = dfs(root->left, x, parent);
if (ldeep != -1) return ldeep+1;
parent = root;//回溯, 设置parent
int rdeep = dfs(root->right, x, parent);
if (rdeep != -1) return rdeep+1;

我有一个疑问：上述代码，可否改成如下：

int ldeep = dfs(root->left, x, parent);
parent = root;//回溯, 设置parent
int rdeep = dfs(root->right, x, parent);

if (ldeep != -1) return ldeep+1;
if (rdeep != -1) return rdeep+1;

完全不能，错误，绝对的错误，我第一次就是这样错的，属于什么错误? 返回位置，返回时机控制出现问题。ldeep判断了之后，应该立刻。马上返回。我都傻逼了。不晓得自己咋会写成下面那个傻逼代码。。。

注意：已经找到目标值之后。回溯阶段parent不做任何修改。

再来一道参数设计的题目：用三种方式设计参数解决它。让大家再次感受下递归函数参数的设计性.

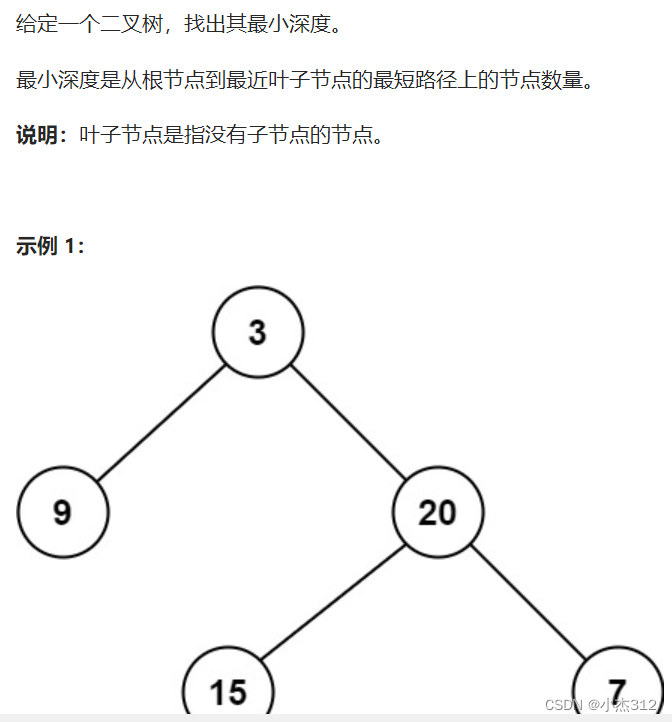
力扣

思路：我知道，这道题最合适的就是广搜。为啥？最低？最小？广搜适合解决最短路径，一切具备最小的距离的那种搜索问题。

但是老实讲。广搜太具有模板性了。所以这个题目我们用深搜来做岂不锻炼自己.

/**
 * 二叉树的最小深度。很明显最简单的方式就是层序了
 * 一层层向下，出现没有孩子结点的结点自然就是最小深度层的叶子结点
 * 
 * 解法 a. 采取的方式是利用无参深度优先搜索
 class Solution {
    int ans = INT_MAX;//记录结果
    void dfs(TreeNode* root, int deep) {
        if (root == nullptr) return;
        if (root->left == nullptr && root->right == nullptr) {//maybe ans
            ans = min(deep, ans);
            return;
        }
        dfs(root->left, deep+1);
        dfs(root->right, deep+1);
        return;
    }

public:
    int minDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        dfs(root, 1);
        return ans;
    }
};
 * 
 *
 * 体现递归函数参数返回值设计性的时候来了.
class Solution {
    //利用返回值获取结果.
    int dfs(TreeNode* root, int deep) {
        if (root == nullptr) return INT_MAX;//说明不是结果.
        if (root->left == nullptr && root->right == nullptr) {
            return deep;//maybe ans;
        }
        int ldeep = dfs(root->left, deep+1);
        int rdeep = dfs(root->right, deep+1);
        return min(ldeep, rdeep);
    }

public:
    int minDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        return dfs(root, 1);
    }
}; 
 * 
 *递归函数参数的设计。有些时候就是区分是真的学懂递归过程的时候.
 * class Solution {
    //利用入参返回结果.
    void dfs(TreeNode* root, int deep, int& ans) {
        if (root == nullptr) return;
        if (root->left == nullptr && root->right == nullptr) {
            ans = min(ans, deep);
            return;
        }
        dfs(root->left, deep+1, ans);
        dfs(root->right, deep+1, ans);
        return;
    }

public:
    int minDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        int ans = INT_MAX;
        dfs(root, 1, ans);
        return ans;
    }
};
*/

三种版本的代码放在这里了。经过上面个的题目打磨。这题，要解决小case.

广度优先搜索 --- 最自然的搜索策略

广度搜索就是那种一面面，一层层，一圈圈的处理。我的感觉就是一种原点扩散。一个原点向外一圈一圈，一层一层的展开。这个就是广度嘛。因为是按照一定的距离，或者权重绕着起点扩散搜索的。所以距离是慢慢扩大的。同一层距离最开始的位置都是一个间距。我靠。说开了。这么一说。其实层序后面的理论都说完了。

广度优先搜索的理论特别的简单。但是他确实一种特别实用的搜索策略。或者遍历策略。最短路径从策略。如果我的感觉没有错误。他跟Dijkstra算法有那么一点异曲同工之妙。只不过Dijkstra算的是权重不是1. 所以不能简单的使用队列来维护这个顺序。需要用到heap堆结构。或者说带权重的队列。优先队列来维护这些结点的搜索，最短路径展开。

Dijkstra理论：

Dijkstra算法根据当前已知的最短路径长度来选择下一个要探索的节点，该选择基于贪心策略：每次选择当前距离起始节点最近的未探索节点。

与BFS相比，Dijkstra算法在以下方面应用了广度优先搜索的思想：

探索顺序：Dijkstra算法按照节点到起始节点的距离递增的顺序进行探索，这与BFS按层级顺序探索的思想相似。
路径更新：在Dijkstra算法中，如果找到了更短的路径来到达某个节点，它会更新该节点的最短路径长度。这类似于BFS在发现更短路径时更新节点的距离。

总之吧：Dijskra和广度优先搜索算法联合起来学习。这个确实可以理解的更为轻松方便。两者有着异曲同工，给我的感觉都是有点贪心的意思。贪心的觉得目的地就应该在自己附近。最近的位置上。区别：

然而，Dijkstra算法与BFS也存在一些关键的区别：

优先级队列：Dijkstra算法使用优先级队列（通常使用最小堆）来选择下一个要探索的节点。这使得它能够根据节点到起始节点的距离进行有效的选择。而BFS则使用FIFO队列，只按照节点的到达顺序进行探索。
权重边：Dijkstra算法考虑了图中边的权重，它通过不断更新节点的最短路径长度来找到最短路径。而BFS通常用于无权图或每条边权重相同的情况。

题目：

力扣

102. 二叉树的层序遍历（算法很单纯，一道足够了）

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> ans;
        if (root == nullptr) return ans;
        queue<TreeNode*> que;
        TreeNode* p = nullptr;
        que.push(root);//入0层结点
        //每一层结点都放进去, 全部放进去
        int deep = 0;
        while (!que.empty()) {
            ans.push_back(vector<int>());//给一层盖房子
            int n = que.size();
            for (int i = 0; i < n; i++) {
                p = que.front(); que.pop();
                ans[deep].push_back(p->val);
                if (p->left) que.push(p->left);
                if (p->right) que.push(p->right);
            }
            deep += 1;//下一层
        }
        return ans;
    }
};

经典的回溯

学习方向：别的不说。一张纸，一支笔，一个空数组，1，2，3.按照不同的情况往里面放置一次，感受感受。这不比直接撸代码强。代码录得再多，终究会忘记。回溯最重视过程。请大家拿起笔和纸，充当人型递归机器。走一步。这特别对于排列组合，回溯问题的解决比啥都强。因为它们都是路径问题呀。这个路径咋走的。我们需要做到心中有数。

46. 全排列
https://leetcode.cn/problems/permutations/description/

77. 组合
https://leetcode.cn/problems/combinations/description/

47. 全排列 II
https://leetcode.cn/problems/permutations-ii/description/

39. 组合总和
https://leetcode.cn/problems/combination-sum/description/

78. 子集
https://leetcode.cn/problems/subsets/description/

90. 子集 II
https://leetcode.cn/problems/subsets-ii/description/

二维矩阵中的广搜与深搜

学习方向：本质还是回溯问题。所以上面的那些题目做完之后，心中对于回溯已经有所认知了。有所认知的基础之下，实践。再认知，再实践。算法。数据结构的学习要有迭代性。

细节点注意：有些适合题目里面有坑，需要提前做个预处理啥的。比如把边上的陆地变成海水呀。啥的。总之，注意细节。方法绝对就那两种搜索。重要的是细节的处理。

经典的二维矩阵的深度搜索

200. 岛屿数量
https://leetcode.cn/problems/number-of-islands/

1020. 飞地的数量
https://leetcode.cn/problems/number-of-enclaves/description/

695. 岛屿的最大面积
https://leetcode.cn/problems/max-area-of-island/description/

37. 解数独
https://leetcode.cn/problems/sudoku-solver/description/

52. N 皇后 II
https://leetcode.cn/problems/n-queens-ii/description/

22. 括号生成
https://leetcode.cn/problems/generate-parentheses/#/description

二维矩阵的广度优先搜索典型例题：

934. 最短的桥
https://leetcode.cn/problems/shortest-bridge/description/

搜索算法的核心就在于在遍历搜索空间所有状态的过程收集特定的路径或者状态的过程。几乎无数算法的基础。如果是一道大家都没有做过的题目，我想大家拿到手上的第一个想法应该都是思考遍历。穷举。在穷举的过程中发现可以利用某一算法思想或是某一快速查找的数据结构对时间复杂度进行降阶。比如单纯的搜索 + 记忆化 + 状态积累。（动态规划）单纯的线性查找 + hash表或者红黑树可以实现 O(1) 或者是 O(logN) 的查找时间复杂度降阶..... 种种迹象，无一不在重复着搜索算法以及穷举思想的重要性.

最好，跟兄弟们建个议，您读了我的文章就是个缘分。哈哈哈。小杰不喜欢被规矩卡死的，天马行空学习的大学生活。但是也不能荒废。学计算机嘛。积累积累积累大过一切。一切东西，当我们的基础深度足够的适合都变得轻松易懂了起来。

算法数据结构学习小心得：会忘，且很快，解决办法，就把自己的一些总结当作数学公式，反复。反复的是那个思路，不是那段代码。最好，祝看见这篇文章的兄弟工作的升职加薪，身体健康，学习的学业进步，保研高校。拜拜。咯，算法，暂时这一阶段就到这里了。哈哈哈，下一步，希望可以学习一些工程项目能力，对C++的各种语法糖做一些应用，写一些小框架，小轮子，为未来做打算，做沉淀。 ----