目录
经典SVM
软间隔SVM
核SVM
SVM分类器应用于人脸识别
SVM优点
SVM缺点
经典SVM
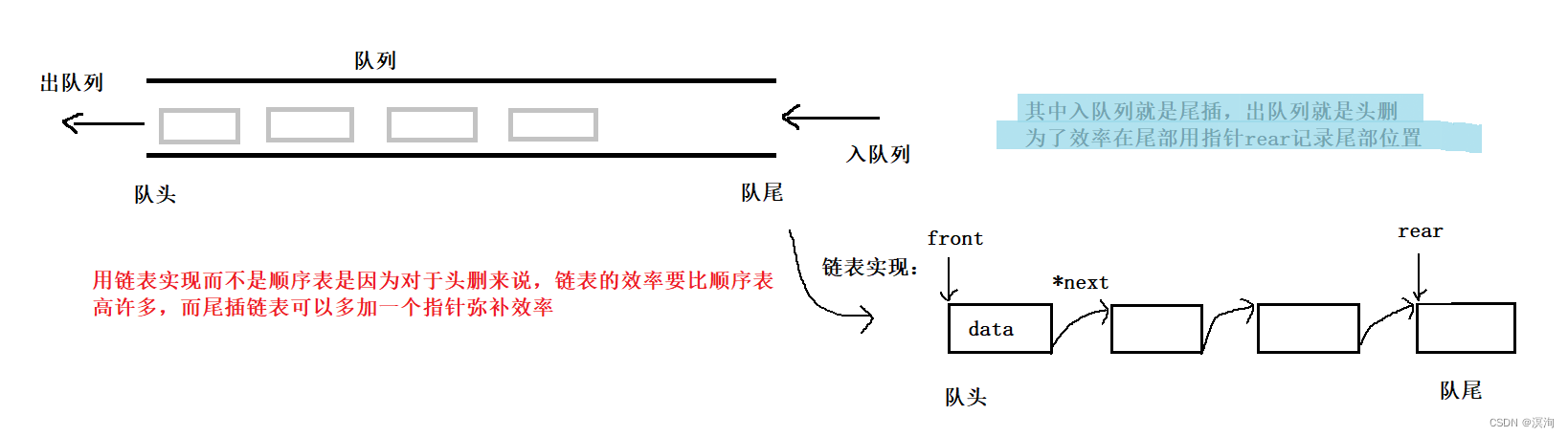
支持向量机(Support Vector Machine,SVM)是一种二分类模型,其基本思想是在特征空间中找到一个最优的超平面,使得正负样本点到该超平面的距离最大化,从而实现对样本的分类。


软间隔SVM

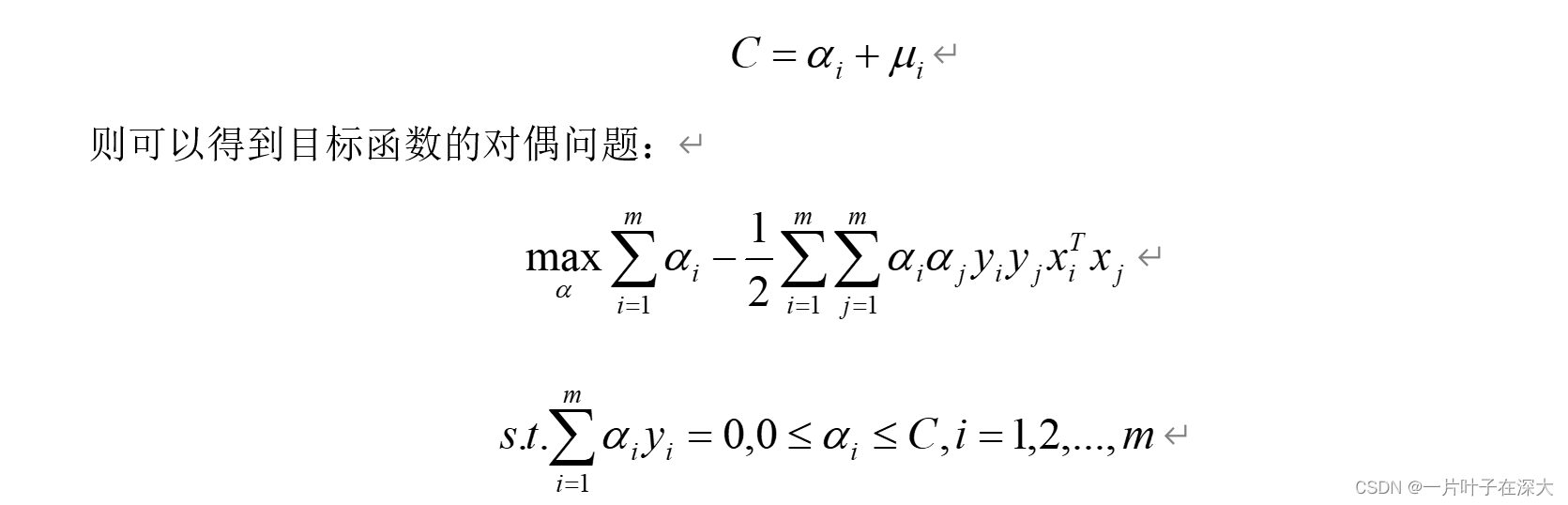
核SVM


SVM分类器应用于人脸识别
经典SVM为二分类模型,对于多分类模型,可以通过以下两种方法实现:
①One-vs-One(OVO):将每个类别之间的所有可能组合都训练一个二元分类器,然后通过投票或者加权投票来决定最终的分类结果。
②One-vs-All(OVA):将一个类别作为正例,其余所有类别作为负例,训练一个二元分类器,然后重复这个过程,直到每个类别都有一个分类器。最后通过投票或者加权投票来决定最终的分类结果。
对于人脸识别,SVM是用来分类的,我们可以使用像PCA、LDA、LPP、NPE等降维算法先进行数据降维再分类。
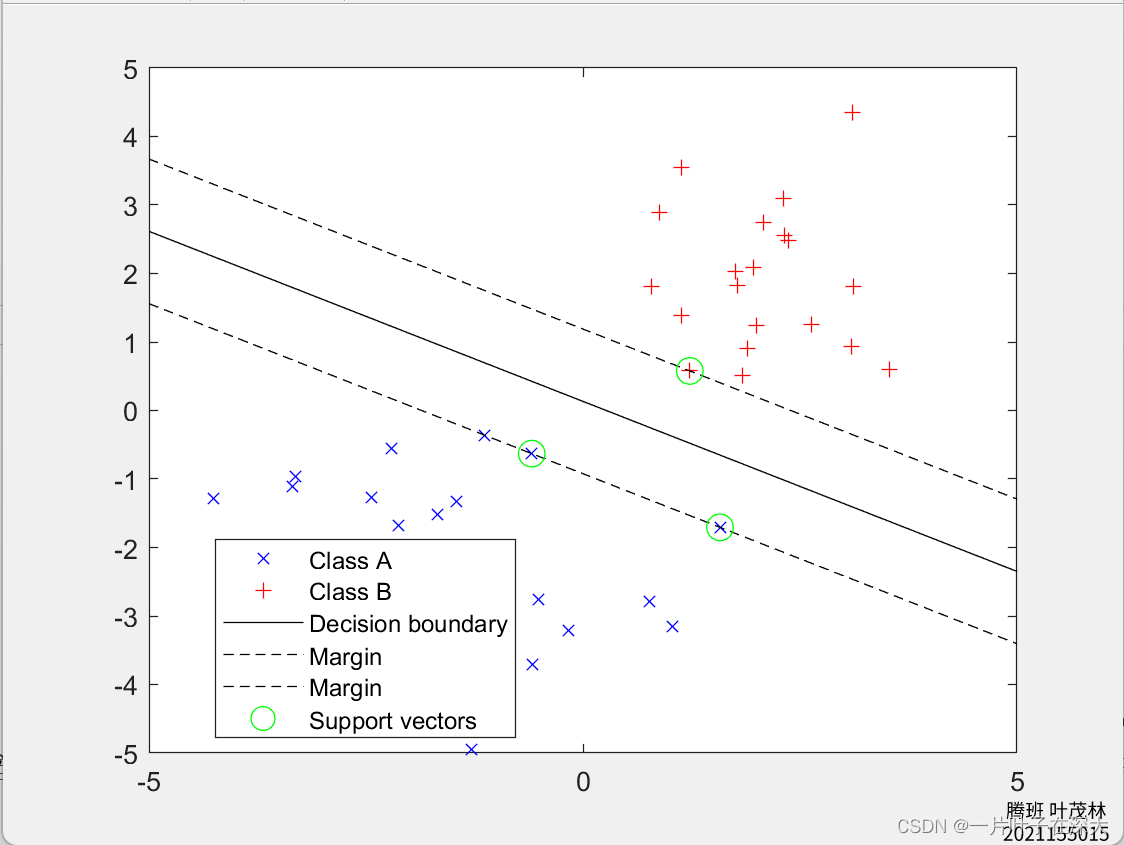
SVM二分类代码,即文章开头的图片示例matlab代码:
% 生成随机数据
X = [randn(20,2)-2; randn(20,2)+2]; % 生成20个标签为-1的点和20个标签为1的点,分别在(-4,-4)和(4,4)的区域内
Y = [-1*ones(20,1); ones(20,1)]; % 将标签存入列向量y中
% 拟合SVM模型
svmModel = fitcsvm(X,Y); % 拟合线性SVM模型
% 绘制决策边界
w = svmModel.Beta; % 获取模型的权重向量w
b = svmModel.Bias; % 获取模型的偏置项b
a = -w(1)/w(2); % 计算决策边界的斜率
xx = linspace(-5,5); % 生成x坐标
yy = a*xx - b/w(2); % 计算决策边界的y坐标
margin = 1/sqrt(sum(w.^2)); % 计算间隔边界的宽度
yy_down = yy - sqrt(1+a^2)*margin; % 计算下界的y坐标
yy_up = yy + sqrt(1+a^2)*margin; % 计算上界的y坐标
% 绘制数据点和支持向量
figure; % 创建新的图形窗口
gscatter(X(:,1),X(:,2),Y,'br','x+'); % 绘制数据点,标签为-1的点用蓝色表示,标签为1的点用红色表示
hold on; % 将图形保持在当前状态,以便绘制其他图形
plot(xx,yy,'k-'); % 绘制决策边界
plot(xx,yy_down,'k--'); % 绘制间隔边界下界
plot(xx,yy_up,'k--'); % 绘制间隔边界上界
plot(svmModel.SupportVectors(:,1),svmModel.SupportVectors(:,2),'go','MarkerSize',10); % 绘制支持向量,用黑色圆点表示
axis([-5 5 -5 5]); % 设置坐标轴范围
legend('Class A','Class B','Decision boundary','Margin','Margin','Support vectors'); % 设置图例
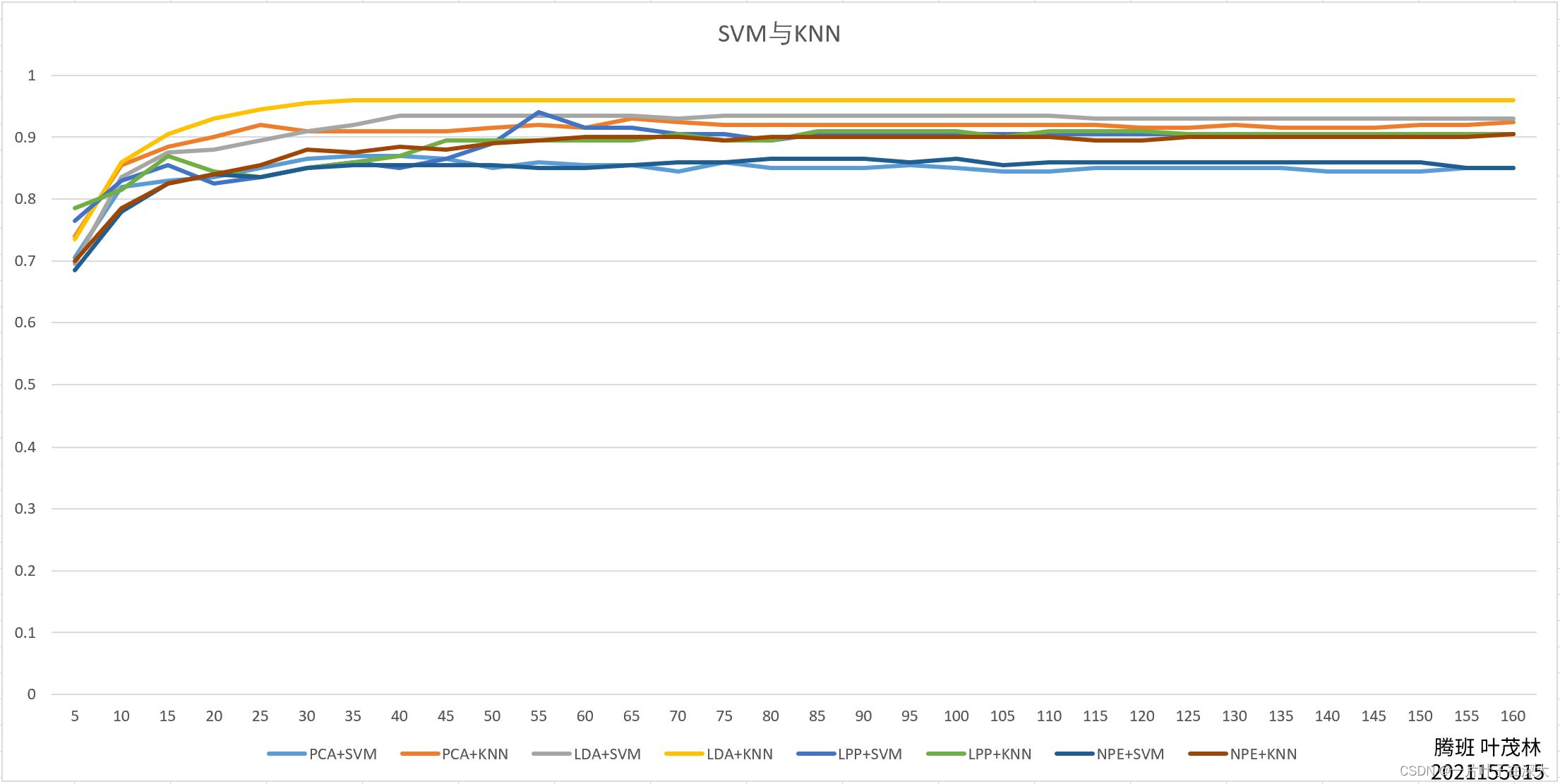
hold off; % 关闭当前图形的保持状态,以便绘制其他图形人脸识别多分类,使用OVO模式训练SVM模型,构建标签矩阵后进行模型训练,然后将数据写入excel表格,我这里的代码例子是先用PCA进行降维的,所以写入PCA.xlsx文件中。
halfDataNumber=pictureNumber/2;
Y=zeros(halfDataNumber,1);
for i=1:halfDataNumber
Y(i)=floor((i-1)/testNumber)+1;
end
for dimension=5:5:160
egienvector=egienvectors(:,1:dimension);
trainDataTemp=egienvector'*trainData;
testDataTemp=egienvector'*testData;
right=0;
model=fitcecoc(trainDataTemp',Y);
YPredicted=predict(model,testDataTemp');
for i=1:halfDataNumber
if Y(i)==YPredicted(i)
right=right+1;
end
end
rate=right/halfDataNumber;
SVMresult=[SVMresult,rate];
end
X=5:5:160;
plot(X,SVMresult);
writematrix(SVMresult,'PCA.xlsx');SVM优点
优点:
- 高效性:SVM在处理高维度数据和样本数量较少的情况下表现出色,因为它只关注支持向量,而不受非支持向量的影响。
- 可解释性:SVM提供了对分类结果的良好解释能力。支持向量可以帮助我们了解决策边界及分类结果的原因。
- 鲁棒性:SVM对于处理输入空间中的噪音和异常值具有较好的鲁棒性。由于它的决策函数只依赖于支持向量,所以局部的扰动并不会对整体模型产生很大影响。
- 泛化能力:SVM通过最大化间隔来选择最优决策边界,从而提高了模型的泛化能力。这种特性使得SVM在处理未见过的数据时表现较好。
SVM缺点
缺点:
- 参数调优困难:SVM中的核函数和正则化参数需要事先进行合理设置,而且对于不同的问题,最优的参数往往是不同的,因此调优可能需要耗费大量的时间和计算资源。
- 计算复杂度高:当样本量很大时,SVM的计算复杂度会显著增加,尤其是在使用非线性核函数时。这可能导致训练时间较长,并且在大规模数据集上的应用受到限制。
- 对缺失数据敏感:SVM对于缺失数据较为敏感,因为它主要依赖于支持向量,如果包含缺失值的样本成为支持向量,则可能会影响模型的性能。
- 难以处理多分类问题:原始的SVM算法是二分类算法,要将其扩展到多类别问题,通常需要借助一些技巧,如一对多(One-vs-Rest)或一对一(One-vs-One)策略。