假设我们有一个关于餐厅顾客的数据集，其中包括9个样本，每个样本有3个属性：天气、是否有预订和是否是周末，以及一个类别标签，表示该顾客是否会来餐厅（是或否)。

数据集如下：

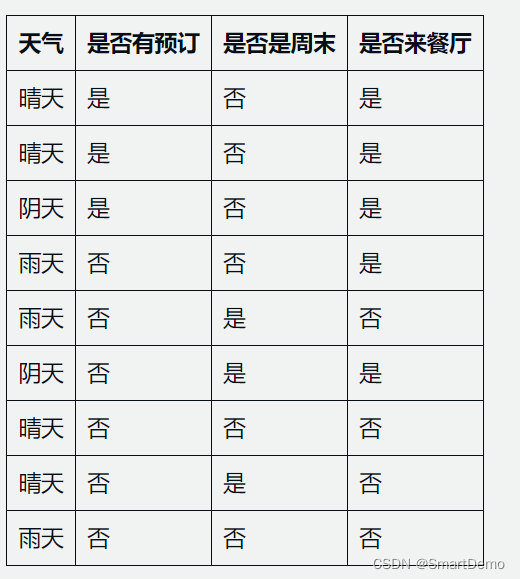
使用C4.5算法来构建决策树。

1、首先，计算整个数据集的信息熵，公式为：

 

其中， 表示类别的个数，表示样本属于第  个类别的概率。

在本例中:

因此，整个数据集的信息熵为：

2、接下来，计算每个属性的信息增益比。

以天气为例，计算其信息增益比的公式为：

其中

 ：表示属性

： 表示属性  的信息增益

 ：表示属性  的固有值

计算公式为：

其中：

 ：表示属性  的取值个数

 ：表示选出属性  取值等于  的样本集合

在本例中，天气有三个取值，即晴天、阴天和雨天，因此 

我们可以根据数据集中天气的取值，将数据集划分为三个子集：

• 子集1：天气=晴天。该子集有5个样本，其中2个会来餐厅，3个不会来。
• 子集2：天气=阴天。该子集有2个样本，其中2个会来餐厅
• 子集3：天气=雨天。该子集有2个样本，其中1个会来餐厅，1个不会来。

计算子集1、子集2和子集3的信息熵：

计算天气的信息增益和固有值：

因此，天气的信息增益比为：

同样地，我们可以计算出其他属性的信息增益比，结果如下：

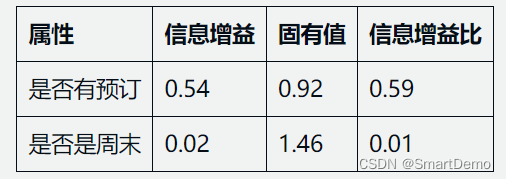
由于是否有预订的信息增益比最大，因此我们选择是否有预订作为划分属性，将数据集划分为有预订和无预订两个子集。

对于有预订的子集，其中所有样本都会来餐厅，因此我们可以将其转换为一个叶子节点，并赋予类别标签“是”；

对于无预订的子集，需要继续递归地执行上述步骤，直到所有子集都被转换为叶子节点。

最终的决策树如下：

是否有预订 = 是: 是
是否有预订 = 否:
|   天气 = 晴天: 否
|   天气 = 阴天: 是
|   天气 = 雨天: .....