算法之动态规划系列（基础篇）

一、前置基础
二、题目-- 爬楼梯
- 2.1、思路
- 2.2 代码实现
三、题目--杨辉三角
- 3.1、思路
- 3.2、代码实现
四、题目--买卖股票的最佳时机
- 4.1、思路
- 4.2、代码实现
- 4.3、优化
五、比特位计数
- 5.1、思路
- 5.2、代码实现（最高有效位法）
- 5.3、代码实现（最低有效位法）：
总结

一、前置基础

动态规划，需要清楚如下：

dp数组的含义以及dp下标的含义。
递推公式。
dp数组如何初始化。
遍历顺序，如果是两个for循环，清晰先循环哪一个。
如果算法执行有问题，打印dp数组分析。

以下题目来源：力扣（LeetCode）

二、题目-- 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1）1 阶 + 1 阶
2）2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1） 1 阶 + 1 阶 + 1 阶
2） 1 阶 + 2 阶
3） 2 阶 + 1 阶

2.1、思路

像这种求多少种可能性的题目一般都有递推性质，即f(n)和f(n-1)…f(1)之间是有联系的： f(n)=f(n-1)+f(n-2)。可转化为求斐波那契数列第n项的值，唯一的不同在于起始数字不同。

用动态规划：

建立一维数组dp[2]，下标分别对应的前一个的值。
递推公式：f(n)=f(n-1)+f(n-2)；其中f(0)=1,f(1)=1。
dp初始化：dp[0]=1，dp[1]=1。
只需要一个循环体。

2.2 代码实现

class Solution {
public:
    int climbStairs(int n) {
        if(n<2)
            return 1;
        int dp[2];
        dp[0]=1;
        dp[1]=1;
        int tmp;
        for(int i=2;i<=n;i++)
        {
            tmp=dp[0];
            dp[0]=dp[1];
            dp[1]=dp[0]+tmp;
        }
        return dp[1];
    }
};

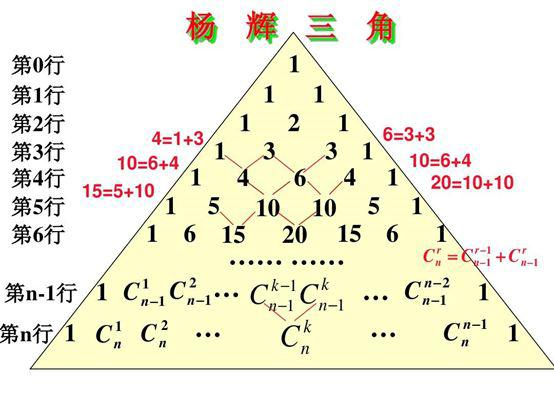
三、题目–杨辉三角

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:

输入: numRows = 1
输出: [[1]]

3.1、思路

杨辉三角具有以下性质：

每行数字左右对称，由 1 开始逐渐变大再变小，并最终回到 1。
第 n 行（从 0 开始编号）的数字有 n+1 项，前 n 行共有 $\frac{n(n+1)}{2}$ 个数。
第 n 行的第 m 个数（从 0 开始编号）可以被表示为组合数 C(n,m) ，记作 $\mathcal{C}_n^m$ 或 $\binom{n}{m}$ ，即从 n 个不同元素中取 m 个元素的组合数。可以用公式来表示它： $\mathcal{C}_n^m=\dfrac{n!}{m!\times (n-m)!}$ 。
每个数字等于上一行的左右两个数字之和，可用此性质写出整个杨辉三角。即第 n 行的第 i 个数等于第 n-1行的第 i-1个数和第 i 个数之和。这也是组合数的性质之一，即 $\mathcal{C}_n^i=\mathcal{C}_{n-1}^i+\mathcal{C}_{n-1}^{i-1}$ 。
$a+b)^n$ 的展开式（二项式展开）中的各项系数依次对应杨辉三角的第 n 行中的每一项。

根据性质，可以进行动态规划设计：

建立二维数组，用来存储杨辉三角的每一行数字，下标是杨辉三角的具体数字。
递推公式可以解释为：dp[i][j]=dp[i-1][j-1]+dp[i-1][j]；即前一项的数组前一项的相加。
数组初始化，杨辉三角的性质是当前行的第一项和最后一项都是1，因此dp[i][0]=dp[i][max]=1。
需要两个循环体，先遍历行，再遍历列；在遍历列时，相当于一维数组的动态规划。

3.2、代码实现

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> res;//动态规划的二维数组
        
        for(int i=0;i<numRows;i++)
        {
            vector<int> tmp(i+1);
            // 初始化
            tmp[0]=1;
            tmp[i]=1;
            for(int j=1;j<i;j++)
            {
                tmp[j]=res[i-1][j-1]+res[i-1][j];
            }
            res.emplace_back(tmp);
        }
        return res;
    }
};

四、题目–买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择某一天买入这只股票，并选择在未来的某一个不同的日子卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

4.1、思路

题目只问最大利润，没有问这几天具体哪一天买、哪一天卖，因此可以考虑使用动态规划的方法来解决。

买卖股票有约束，根据题目意思，有以下两个约束条件：

条件 1：你不能在买入股票前卖出股票；
条件 2：最多只允许完成一笔交易。

因此当天是否持股是一个很重要的因素，而当前是否持股和昨天是否持股有关系，为此我们需要把是否持股设计到状态数组中。

状态定义：dp[i][j]是下标为 i 这一天结束的时候，手上持股状态为 j 时，我们持有的现金数。也就是说dp[i][j] 表示天数 [0, i] 区间里，下标 i 这一天状态为 j 的时候能够获得的最大利润。其中：

j = 0，表示当前不持股；
j = 1，表示当前持股。

推导状态转移方程：

dp[i][0]：规定了今天不持股，有以下两种情况：

昨天不持股，今天什么都不做；
昨天持股，今天卖出股票（现金数增加），

dp[i][1]：规定了今天持股，有以下两种情况：

昨天持股，今天什么都不做（现金数与昨天一样）；
昨天不持股，今天买入股票（注意：只允许交易一次，因此手上的现金数就是当天的股价的相反数）。

4.2、代码实现

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n=prices.size();
        if(n<2)
            return 0;
        vector<vector<int>> dp(n,vector<int>(2));
        // dp[i][0] 下标为 i 这天结束的时候，不持股，手上拥有的现金数
        // dp[i][1] 下标为 i 这天结束的时候，持股，手上拥有的现金数
        dp[0][0]=0;
        dp[0][1]=-prices[0];
        for(int i=1;i<n;i++)
        {
            dp[i][0]=max(dp[i-1][0],prices[i]+dp[i-1][1]);
            dp[i][1]=max(dp[i-1][1],-prices[i]);
        }
        return dp[n-1][0];
        

    }
};

4.3、优化

空间优化只看状态转移方程。

状态转移方程里下标为 i 的行只参考下标为 i - 1 的行（即只参考上一行），并且：

下标为 i 的行并且状态为 0 的行参考了上一行状态为 0 和 1 的行；
下标为 i 的行并且状态为 1 的行只参考了上一行状态为 1 的行。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n=prices.size();
        if(n<2)
            return 0;
        int dp[2];
        dp[0]=0;
        dp[1]=-prices[0];
        for(int i=1;i<n;i++)
        {
            dp[0]=max(dp[0],prices[i]+dp[1]);
            dp[1]=max(dp[1],-prices[i]);
        }
        return dp[0];
    }
};

五、比特位计数

给一个整数 n ，对于 0 <= i <= n 中的每个 i ，计算其二进制表示中 1 的个数，返回一个长度为 n + 1 的数组 ans 作为答案。

示例 1：

输入：n = 2
输出：[0,1,1]
解释：
0 --> 0
1 --> 1
2 --> 10

示例 2：

输入：n = 5
输出：[0,1,1,2,1,2]
解释：
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101

5.1、思路

第一种：最高有效位法。在区间[0,i]中找到一个数y，y ≤ i，且y的最高位为1而其他位都为0（y&(y-1)==0），那么就可以计算bit[i]=bit[i-y]+1。

第二种：最低有效位。第一种方法需要实时维护最高有效位，当遍历到的数是2的整数次幂时，需要更新最高有效位。对于正整数 xx，将其二进制表示右移一位，等价于将其二进制表示的最低位去掉，得到的数是
。如果 $\textit{bits}\big[\lfloor \frac{x}{2} \rfloor\big]$ 的值已知，则可以得到 $\textit{bits}[x]$ 的值：bits[x]= $\textit{bits}\big[\lfloor \frac{x}{2} \rfloor\big]$ +(x&1)。

第三种：最低设置位。推导公式：bits[x]=bits[x&(x−1)]+1。

5.2、代码实现（最高有效位法）

class Solution {
public:
    vector<int> countBits(int n) {
        vector<int> ans(n+1);
        ans[0]=0;
        int hightbit=0;//维护最高有效位
        for(int i=1;i<=n;i++)
        {
            if((i&(i-1))==0)
                hightbit=i;
            ans[i]=ans[i-hightbit]+1;
        }
        return ans;
    }
};

5.3、代码实现（最低有效位法）：

class Solution {
public:
    vector<int> countBits(int n) {
        vector<int> ans(n+1);
        ans[0]=0;
        for(int i=1;i<=n;i++)
        {
            ans[i]=ans[i/2]+(i&1);
        }
        return ans;
    }
};