💥💥💥💞💞💞欢迎来到本博客❤️❤️❤️💥💥💥

📋📋📋本文目录如下:⛳️⛳️⛳️
目录
1 概述
2 电力系统潮流计算概述
2.1 电力潮流发展进程
2.2牛顿拉夫逊法潮流计算
4 讲解
4.1 高斯-赛德尔法
4.2 牛顿-拉夫逊法
4.3 快速解耦法
5 Matlab代码实现
1 概述
最初,电力系统潮流计算是通过人工手算的。后来为了适应电力系统日益发展的需要,计算机网络已经形成,为了电力系统的潮流计算提供了物质基础。电力系统潮流计算是电力系统分析计算中最基本的内容,也是的电力系统运行及设计中必不可少的工具。根据系统给定的运行条件、网络接线及元件参数,通过潮流计算可以确定各母线电压的幅值及相角、各元件中流过的功率、整个系统的功率损耗等。
在电力系统规划的设计和现有电力系统运行方式的研究中,都需要利用潮流计算来定量的分析比较供电方案或运行方式的合理性、可靠性和经济性。此外,电力系统的潮流计算也是计算机系统动态稳定和静态稳定的基础,所以潮流计算是研究电力系统的一种很重要和基础的计算。它的发展主要围绕这样几个方面:计算方法的收敛性、可靠性;计算速度的快速性;对计算机存储容量的要求以及计算的方便、灵活等。
本文通过介绍基于牛顿拉夫逊法、高斯赛德尔法及快速解耦法的潮流计算,在MATLAB中进行仿真计算。
2 电力系统潮流计算概述
2.1 电力潮流发展进程
最初,电力系统潮流计算是通过人工计算的。后来为了适应电力系统日益发展的需要,采用了交流计算台。随着电子数字计算机的出现,1956 年 Ward 等人编制了实际可行的计算机潮流计算程序。这样,就为日趋复杂的大规模电力系统提供了极其有力的计算手段。经过几十年的发展,电力系统潮流计算已经十分成熟。电力系统潮流计算形式分为离线计算和在线计算两种。前者主要用于电力系统规划设计、安排系统的运行方式;后者则用于正在运行系统的实时监视和实时控制。在计算原理上离线和在线潮流计算是相同的,都要求满足:(1)计算方法可靠,收敛性好;(2)占用较少的计算机内存;(3)计算速度高;(4)用于界面良好,方便使用。
2.2牛顿拉夫逊法潮流计算
2.2.1节点电压方程
电力网络方程是指将网络的有关参数和变量及其相互关系归纳起来所组成的,可反映网络性能的数学方程式组。不难想象,符合这种方程的有节点电压方程,回路电流方程,割集电压方程等。但由于割集电压方程不常用于电力系统计算,故一般采用节点电压方程或者回路电流方程,但在系统中电流的参量往往比较难以测量和采集,且由于电力系统的等值网络中有较多接地支路,节点电压方程的方程数较少,网络结构改变或变压器变比改变时修改系数也比较方便,故节点电压方程具有其明显的优势。
2.2.2节点导纳矩阵
节点导纳矩阵与节点阻抗矩阵都是方阵,其阶数就等于网络中除参考节点之外的节点数n。但是我们在潮流计算中多采用节点导纳矩阵的原因在于,节点导纳矩阵是稀疏矩阵,其各行非零非对角元数就等于与该行相对节点所连接的不接地支路数。因为节点i 、j 之间无支路直接相连时等于0,这种情况在实际电力系统中非常普遍,所以采用节点导纳矩阵有利于对系统结构进行修改。
对于变压器的等值电路模型,有型等值电路、T型等值变压器模型。但是前两者并不能体现变压器实际具有的电压变换功能,必须将网络中所有参数和变量归算至同一电压等级。但是,等值变压器型模型可等值地体现变压器电压变换功能,也是运用计算机进行电力系统分析时采用的变压器模型,虽然运用这种模型时并不排斥手算。
首先,如图3-2-3(a)所示,变压器的导纳或励磁支路可略去,双绕组变压器可用阻抗与一个理想变压器串联的电路表示。理想变压器只是一个参数,那就是变比。现在变压器阻抗按实际变比归算到低压侧为例,推导出变压器型等值电路。
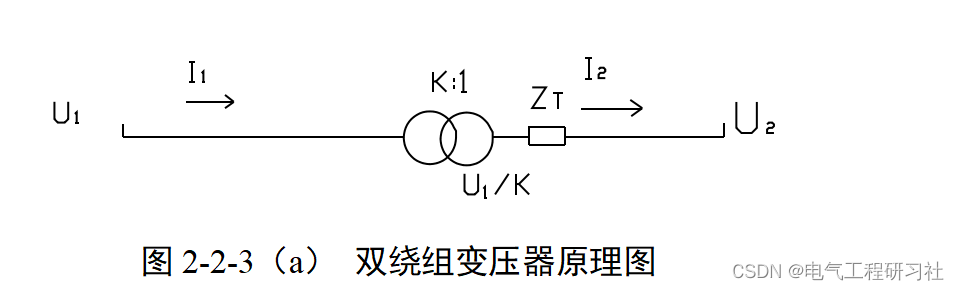
变压器阻抗归算到低压侧等值模型流入和流出理想变压器的功率相等:
其余详细文章见第五部分:

4 讲解

4.1 高斯-赛德尔法

4.2 牛顿-拉夫逊法
4.3 快速解耦法
对于变压器的等值电路模型,有型等值电路、T型等值变压器模型。但是前两者并不能体现变压器实际具有的电压变换功能,必须将网络中所有参数和变量归算至同一电压等级。但是,等值变压器型模型可等值地体现变压器电压变换功能,也是运用计算机进行电力系统分析时采用的变压器模型,虽然运用这种模型时并不排斥手算。