1 二分法

二分法（Binary Search）是一种在有序数组中查找特定元素的搜索算法。它的基本思想是将数组从中间分割，然后判断目标元素与中间元素的大小关系，以确定目标元素在左半部分还是右半部分。然后再在相应的子数组中继续进行同样的操作，直到找到目标元素或确定目标元素不存在。

具体步骤如下：

将数组的左边界设为 left，右边界设为 right。
计算中间位置 mid，即 mid = (left + right) / 2。
比较目标元素与中间元素的大小关系：
如果目标元素等于中间元素，则找到目标元素，返回其索引。
如果目标元素小于中间元素，则更新右边界 right = mid - 1，并继续在左半部分进行二分查找。
如果目标元素大于中间元素，则更新左边界 left = mid + 1，并继续在右半部分进行二分查找。
重复步骤 2 和步骤 3，直到找到目标元素或左边界大于右边界。

时间复杂度O(logN)，其中 n 是数组的长度。由于每次都将搜索范围减半，因此算法的效率非常高。但要求数组是有序的，否则无法应用二分法进行查找。

1.1 在`有序`数组中查找特定元素

基本思想是通过比较中间元素与目标元素的大小关系，将查找范围缩小一半，直到找到目标元素或查找范围为空为止。

因为比如说数组个数为N=16, 最差的情况要分 4 次 $\to [4|4] \to [2|2] \to [1|1] )$ ，而 $4 = log_216$ 。即时间复杂度为 $O (l o g N)$

/* 注意：题目保证数组不为空，且 n 大于等于 1 ，以下问题默认相同 */
int binarySearch(std::vector<int>& arr, int value)
{
    int left = 0;
    int right = arr.size() - 1;
    // 如果这里是 int right = arr.size() 的话，那么下面有两处地方需要修改，以保证一一对应：
    // 1、下面循环的条件则是 while(left < right)
    // 2、循环内当 array[middle] > value 的时候，right = middle

    while (left <= right)
    {
        int middle = left + ((right - left) >> 1);  // 不用right+left，避免int溢出，且更快
        if (array[middle] > value)
            right = middle - 1;
        else if (array[middle] < value)
            left = middle + 1;
        else
            return middle;
        // 可能会有读者认为刚开始时就要判断相等，但毕竟数组中不相等的情况更多
        // 如果每次循环都判断一下是否相等，将耗费时间
    }
    return -1;
}

留意 left + ((right - left) >> 1) 结果等用于(right + left) / 2，但更快，且不会int溢出

1.2 在一个有序数组中查找>=某个数的最左侧的位置

思路依然是二分法，不同于查找某个值找到目标值就停止二分，找最左/右侧位置问题一定是二分到底


int nearLeftSearch(const std::vector<int>& arr, int target)
{
	int left = 0;
	int right = arr.size() - 1;
	int result = -1;
	
	while (left <= right)
	{
		int mid = left + ((right - left) >> 1);
		if (target <= arr[mid]){ // 目标值小于等于mid，就要往左继续找
			result = mid;// 暂时记录下这个位置，因为左边可能全都比目标值小了，就已经找到了
			right = mid - 1;
		} else{		// target > arr[mid]
			left = mid + 1;
		}
	}
	return result;
}

1.3 在一个有序数组中查找<=某个数最右侧位置

如果中间元素大于目标值，说明目标值应该在左半部分，因此我们将搜索范围缩小到左半部分，将 right 更新为 mid - 1。
如果中间元素小于或等于目标值，说明目标值应该在右半部分或就是当前位置，因此我们更新 result 为当前中间索引 mid，以便记录找到的最右侧位置，并将搜索范围缩小到右半部分，将 left 更新为 mid + 1。

int nearRightSearch(const std::vector<int>& arr, int target) 
{
    int left = 0;
    int right = arr.size() - 1;
    int result = -1;

    while (left <= right) {
        int mid = left + (right - left) / 2;

        if (target < arr[mid]) {
            right = mid - 1;
        } else {	// target >= arr[mid]
            result = mid;
            left = mid + 1;
        }
    }

    return result;
}

1.4 局部最小值问题（无序数组使用二分法的案例）

数组arr无序，任意相邻的两个数不等，求一个局部最小的位置（极小值），要求时间复杂度优于O(N)

无序也能二分，只要目标问题在某一边必有解，另一边无所谓，就能够使用二分

1.先判断数组两个边界

如果左边界arr[0] < arr[1]，已找到
如果有边界arr[n-1] < arr[n-2]，已找到
如果两个边界都不是局部最小，又因为任意相邻的两个数不等，则左边界局部单调递减，右边界处局部单调递增。所以在数组内，必然有极小值点

2.进行二分，判断mid与相邻位置的关系，分为3种情况：（提醒：数组中相邻两个元素是不相等的！）
在这里插入图片描述
3.重复过程2直到找到极小值

int LocalMinimumSearch(const std::vector<int>& arr) 
{
    int n = arr.size();
    // 先判断元素个数为0，1的情况，如果题目给出最少元素个>1数则不需要判断
    if (n == 0) return -1;
    if (n == 1) return 0; // 只有一个元素，则是局部最小值
	
	if (arr[0] < arr[1]) return 0;
	
	int left = 0;
    int right = n - 1;
	// 再次提醒，数组中相邻两个元素是不相等的！
    while (left < right) 
    {
        int mid = left + ((right - left) >> 1);

        if (arr[mid] < arr[mid - 1] && arr[mid] < arr[mid + 1]) {
            return mid;  // 找到局部最小值的位置
        } else if (arr[mid - 1] < arr[mid]) {
            right = mid - 1;  // 局部最小值可能在左侧
        } else {
            left = mid + 1;  // 局部最小值可能在右侧
        }
    }

    // 数组中只有一个元素，将其视为局部最小值
    return left;
}

2 简单的递归思想

来自左哥P4开头部分，属于归并排序的前置知识。这里也用到二分法。主要是理解执行过程

例题：在数组的指定范围上求最大值，利用递归实现

#incldue <vector>
#include <algorithm>
int process(const std::vector<int>& arr, int L, int R)
{
	if (L == R) return arr[L]; 
	
	int mid = L + ((R - L) >> 1);	// 求中点,右移1位相当于除以2
	int leftMax = process(arr, L, mid);
	int rightMax = process(arr, mid + 1, R);
	return std::max(leftMax, rightMax);
}

当调用 process(arr, L, R) 函数时，它会执行以下操作：

首先，检查递归终止条件。如果 L 和 R 相等，表示递归到了数组的最小区间，只有一个元素。这时直接返回该元素 arr[L]。
如果没有满足终止条件，说明需要继续进行递归。首先，计算中点 mid，将区间 [L, R] 平分为两个子区间 [L, mid] 和 [mid+1, R]。
然后，递归调用 process(arr, L, mid)，处理左子区间。这一步会将当前函数压栈，进入一个新的递归层级。
在新的递归层级中，再次执行步骤 1-3，直到满足终止条件，返回左子区间的最大值 leftMax。
接着，递归调用 process(arr, mid+1, R)，处理右子区间。同样地，这一步会将当前函数压栈，进入另一个新的递归层级。
在新的递归层级中，再次执行步骤 1-3，直到满足终止条件，返回右子区间的最大值 rightMax。
最后，将左右子区间的最大值 leftMax 和 rightMax 比较，取其中较大的值作为整个区间 [L, R]
的最大值，并将其作为结果返回。
当递归返回到上一层时，将得到的最大值传递给上一层，直到返回到最初的调用点，得到整个数组的最大值。

递归的过程中，每一次递归调用都会创建一个新的函数栈帧，保存函数的局部变量和参数。当满足终止条件时，递归开始回溯，逐层返回最终结果，同时每层的局部变量和参数也被销毁，函数栈帧依次出栈。

依赖关系图

假设目标数组是[3, 2, 5, 6, 7, 4]，调用process(0,5)找最大值，形参arr省略不写了
红色数字为process的执行流程，其中省略了std::max的比较并返回的过程

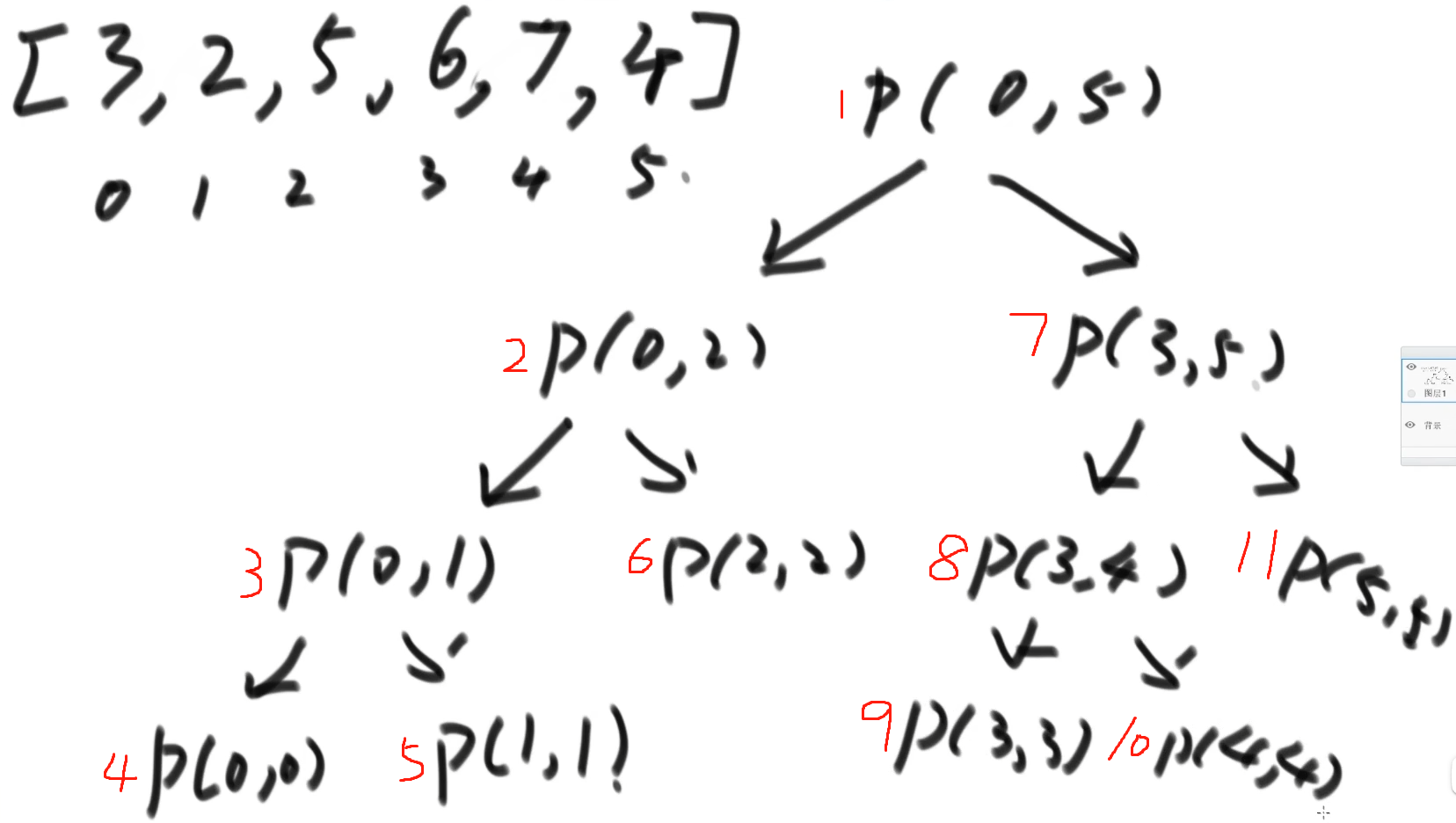
说人话描述这个过程：要想得到数组的返回值，即第1步的返回值，首先要得到2的最大值，而它的最大值根据代码来看要先执行3，同样3又要先执行4，等二分到4这个步骤时，只有一个元素了 L==R，看代码该元素即为当前(0,0)区间的最大值了，返回给3，3拿到leftMax后，还需要右边部分最大值，就执行5，拿到rightMax，最后对左右区间的最大值做比较，拿到(0,1)区间的最大值，又返回给2，2还需要6，6返回后，2比较后得到(0,2)的最大值，返回给1。然后执行右边的。。。。后面就省略了