显然各字符串对 间匹配的先后顺序不影响最大匹配数目, 可以从后往前遍历数组, 判断前面是否有和当前末尾构成匹配的.

class Solution {
public:
    int maximumNumberOfStringPairs(vector<string> &words) {
        int res = 0;        
        while (words.size() > 1) {
            auto &s = words.back();
            reverse(s.begin(), s.end());
            for (int i = words.size() - 2; i >= 0; i--)
                if (s == words[i]) {
                    res++;
                    break;
                }
            words.pop_back();
        }
        return res;
    }
};

记忆化搜索: 定义状态$p_{aa,bb,ab,last}$为剩余三种字符串分别为aa、bb、ab个, 且上一位为last(1代表’A’, 2代表’B’)情况下, 后面可以生成的最长字符串的长度, 枚举可用的三种字符串即可.

class Solution {
public:
    int longestString(int x, int y, int z) {
        int p[x + 1][y + 1][z + 1][3];
        memset(p, -1, sizeof(p));
        function<int(int, int, int, int)> get = [&](int aa, int bb, int ab, int last) {//last: 1->A  2->B
            if (p[aa][bb][ab][last] != -1)
                return p[aa][bb][ab][last];
            p[aa][bb][ab][last] = 0;
            if (aa && last != 1)
                p[aa][bb][ab][last] = max(p[aa][bb][ab][last], 2 + get(aa - 1, bb, ab, 1));
            if (bb && last != 2)
                p[aa][bb][ab][last] = max(p[aa][bb][ab][last], 2 + get(aa, bb - 1, ab, 2));
            if (ab && last != 1)
                p[aa][bb][ab][last] = max(p[aa][bb][ab][last], 2 + get(aa, bb, ab - 1, 2));
            return p[aa][bb][ab][last];
        };
        return get(x, y, z, 0);// last!=1,2 (初始情况没有上一位)
    }
};

动态规划: 定义$p_{i,front,back}$为生成的首位为$front$末位为$back$的$st{r}_i$的最长长度, 若$p_{i,front,back}$状态是可达的, 有两种方式对$p_{i+1,fon{t}^{\prime },bac{k}^{\prime }}$进行更新(对应题中两种操作).

class Solution {
public:
    int minimizeConcatenatedLength(vector<string> &li) {
        int n = li.size();
        int p[n][26][26];//i,front,back
        for (int i = 0; i < n; i++)
            for (int j = 0; j < 26; j++)
                for (int k = 0; k < 26; k++)
                    p[i][j][k] = INT32_MAX;// 标志状态不可达
        p[0][li[0][0] - 'a'][li[0].back() - 'a'] = li[0].size();
        for (int i = 1; i <= n - 1; i++) {
            for (int front = 0; front < 26; front++) {
                for (int back = 0; back < 26; back++)
                    if (p[i - 1][front][back] != INT32_MAX) {
                        p[i][front][li[i].back() - 'a'] = min(p[i][front][li[i].back() - 'a'], p[i - 1][front][back] + (int) (li[i][0] - 'a' == back ? li[i].size() - 1 : li[i].size()));// join(str_(i-1) , li[i])
                        p[i][li[i][0] - 'a'][back] = min(p[i][li[i][0] - 'a'][back], p[i - 1][front][back] + (int) (li[i].back() - 'a' == front ? li[i].size() - 1 : li[i].size())); //join(li[i], str_(i-1))
                    }
            }
        }
        int res = INT32_MAX;
        for (int front = 0; front < 26; front++)
            for (int back = 0; back < 26; back++)
                res = min(res, p[n - 1][front][back]);
        return res;
    }
};

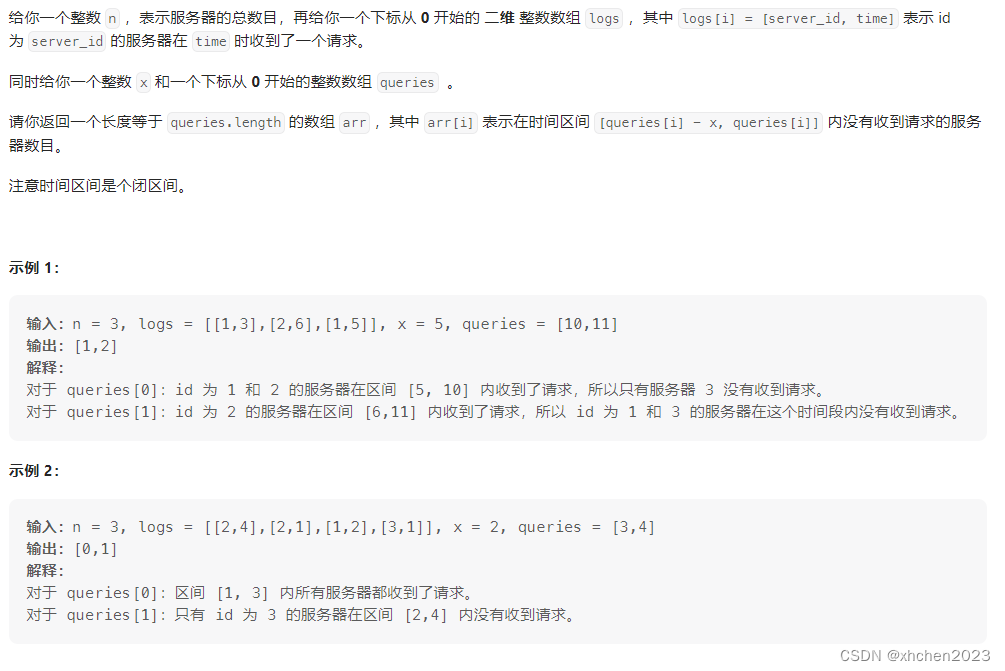
离线查询+双指针: 把日志和查询放在一个有序表$li$中, 并按时间非降序排序, 同时保证相同时间的日志在查询之前. 之后用双指针的方法维护$li$中一段时间差最大为x的区间, 及该区间上不同的服务器个数为$cnt$, 每次移动右指针遇到是查询时, 更新左指针, 对应查询的答案即为$n-cnt$.

class Solution {
public:
    vector<int> countServers(int n, vector<vector<int>> &logs, int x, vector<int> &queries) {
        vector<tuple<int, int, int>> li;// time, type(0:log ,1: query), server_id/query_index
        for (auto &i: logs)
            li.emplace_back(i[1], 0, i[0]);// time, type, server_id
        int m = queries.size();
        for (int i = 0; i < m; i++)
            li.emplace_back(queries[i], 1, i);// time, type, query_index
        sort(li.begin(), li.end());
        unordered_map<int, int> cnt_server;//cnt_server[i] 服务器i当前出现次数
        int cnt = 0;
        vector<int> res(m);
        for (int l = 0, r = 0; r < li.size(); r++) {//遍历li[r]
            if (get<1>(li[r]) == 0) {//log
                int server_id = get<2>(li[r]);
                if (cnt_server[server_id]++ == 0)
                    cnt++;
            } else {//query
                int time_cur = get<0>(li[r]), query_index = get<2>(li[r]);
                for (; get<0>(li[l]) < time_cur - x; l++) {//更新l
                    if (get<1>(li[l]) == 0) {//log
                        if (--cnt_server[get<2>(li[l])] == 0)// 维护cnt_server
                            cnt--;
                    }
                }
                res[query_index] = n - cnt;
            }
        }
        return res;
    }
};