目录
LDA算法
LDA目标
LDA原理推导
LDA除法模型
LDA减法模型
LDA除法正则模型
LDA减法正则模型
证明:St=Sw+Sb
LDA算法流程
LDA优点
LDA缺点
基于LDA的人脸识别
LDA算法
线性判别分析(linear discriminant analysis,LDA),是一种经典的线性学习方法,其原理是:给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近,异类样例的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的直线上,再根据投影点的位置来确定新样本的类别。
LDA作为一种经典的机器学习算法,具有较好的降维效果和分类能力,同时对噪声具有一定的抗干扰能力。然而,LDA也有其局限性,适用于满足其假设条件的线性可分问题。在实际应用中,需要根据具体情况选择合适的算法和方法。
LDA目标
LDA的目标:最小化类内协方差,即让同类投影点尽可能的接近;最大化类间协方差,即让异类投影点尽可能远离。
LDA原理推导
二分类优化

多分类优化
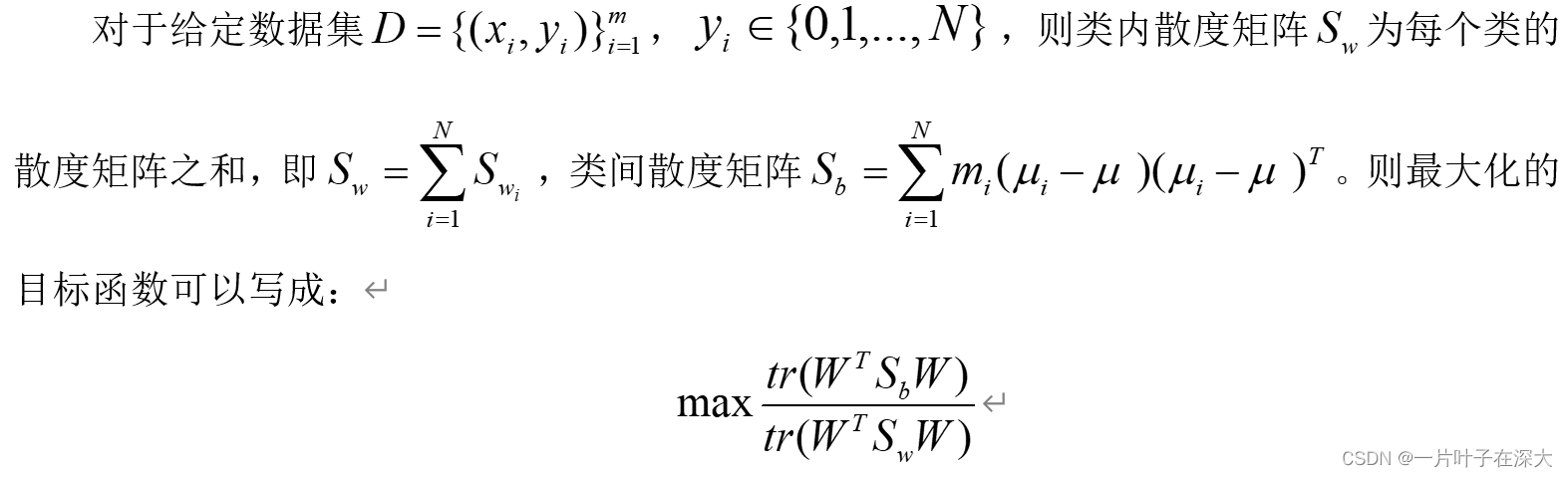

LDA除法模型
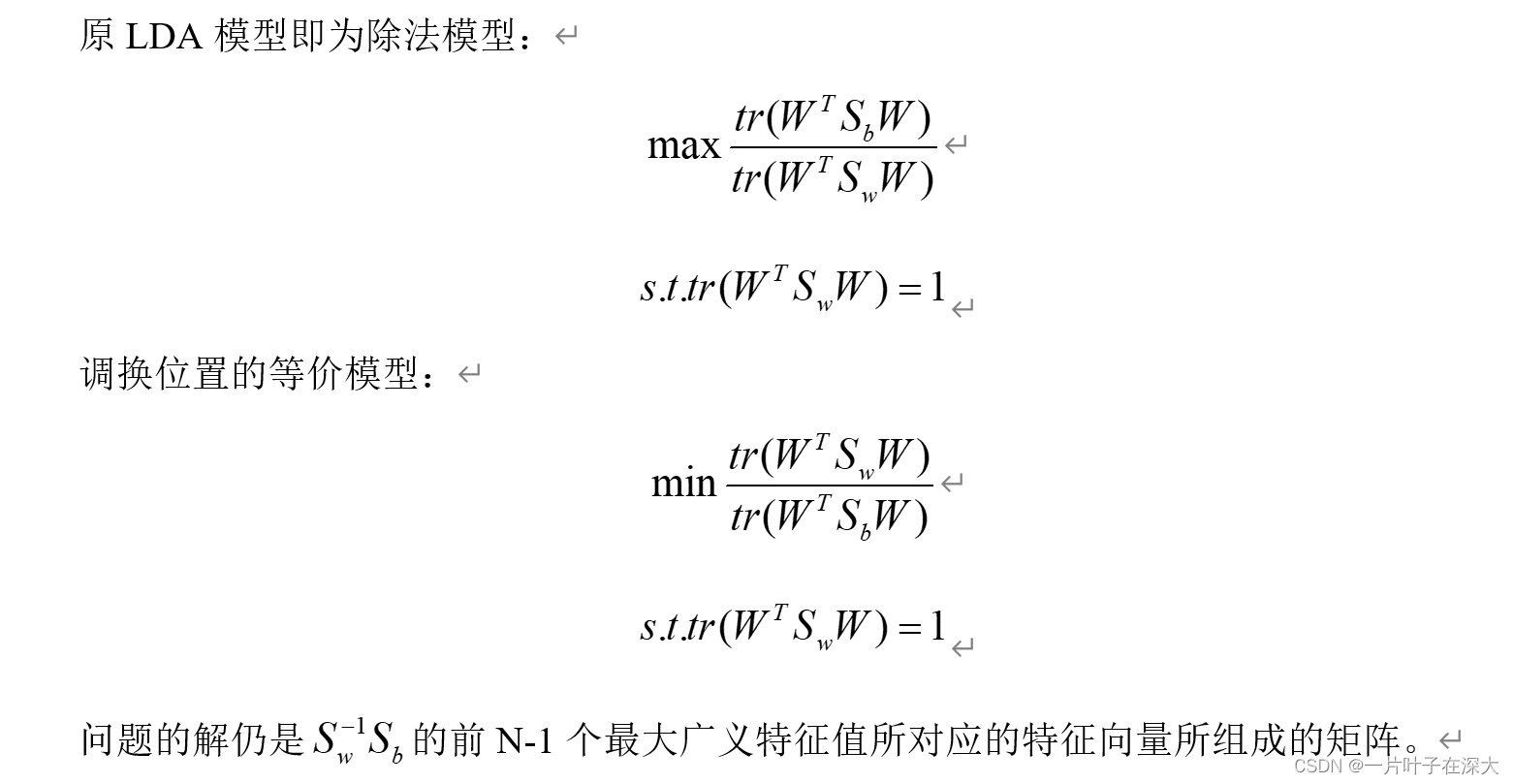
LDA减法模型

LDA除法正则模型

LDA减法正则模型

证明:St=Sw+Sb
证明:
考虑多分类情况,二分类为多分类的一个特例。
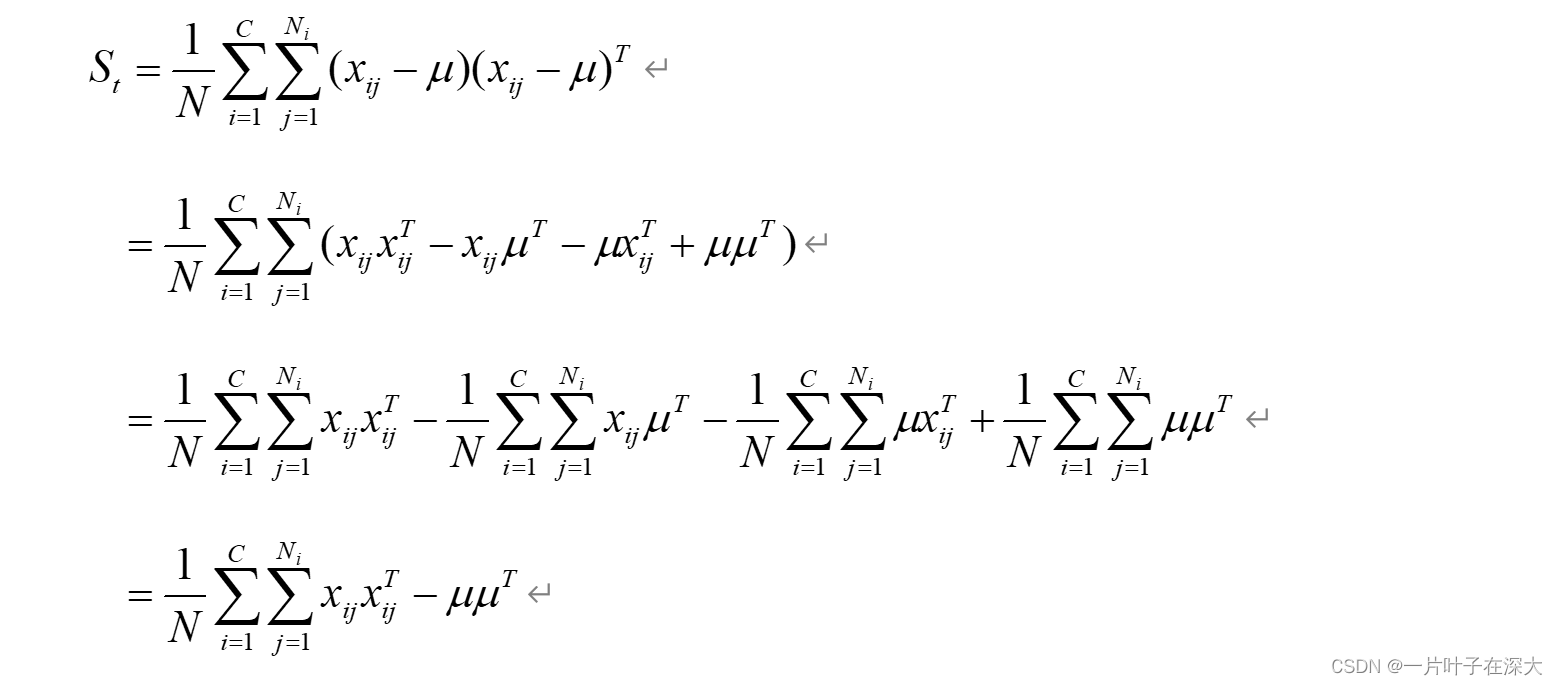
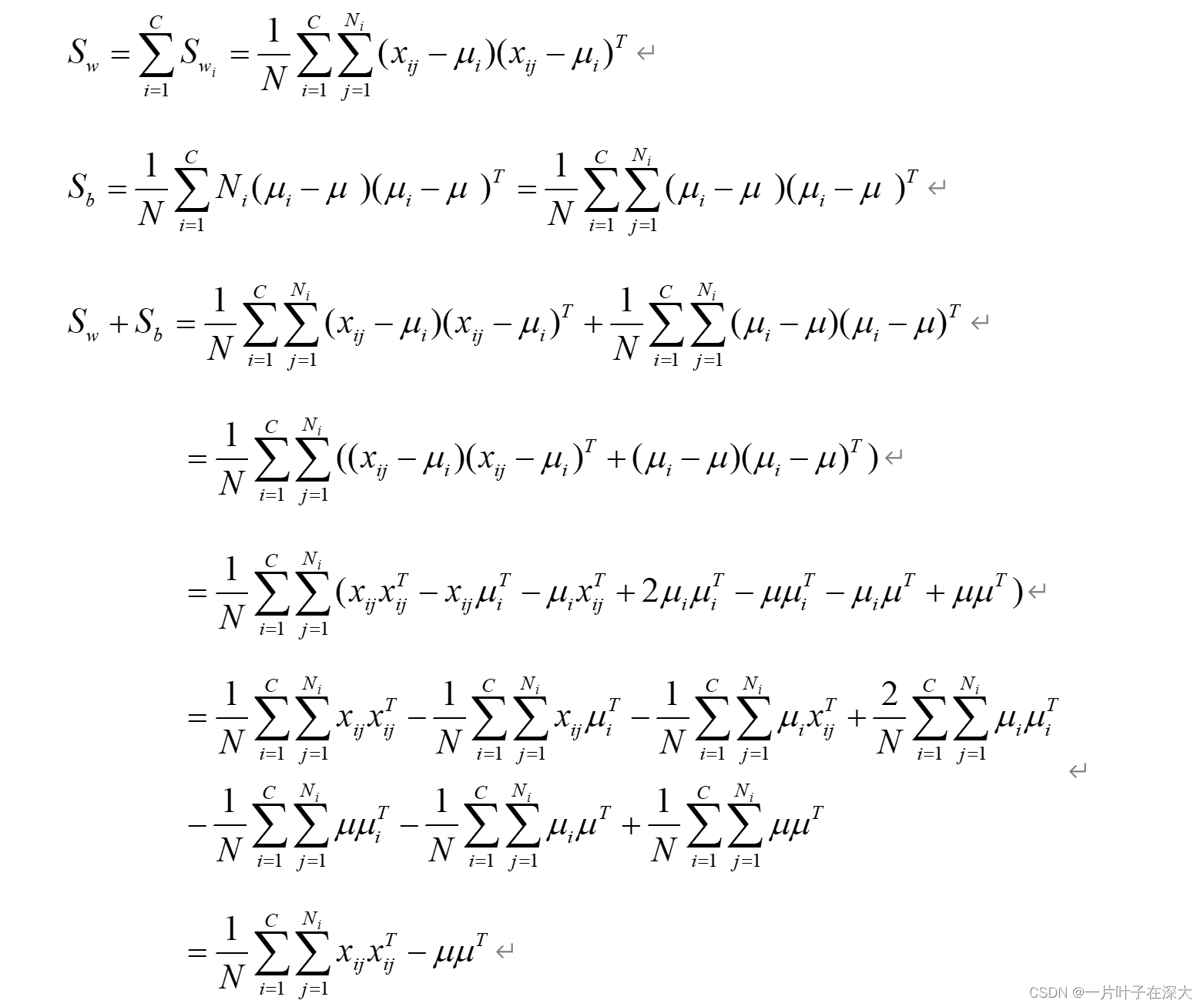
即St=Sw+Sb。
LDA算法流程
下面将逐步介绍LDA步骤:
-
数据准备: 假设我们有N个样本,每个样本有d个特征。同时,这些样本被标记为K个不同的类别。我们将所有样本构成一个矩阵X,其中每一行表示一个样本,第j列表示该样本的第j个特征。对应的类别标签构成向量y。
-
计算类别均值向量: 针对每个类别k,计算其均值向量μ_k。μ_k的第j个元素表示在第j个特征上属于类别k的样本的平均值。
-
计算类内散度矩阵: 类内散度矩阵S_w可以通过计算每个类别内各样本的散布程度来得到。具体地,对于第k个类别,计算其散度矩阵S_k。S_k可以通过将所有属于该类别的样本进行中心化,然后计算协方差矩阵得到。最后,将所有类别的散度矩阵相加,即可得到总的类内散度矩阵S_w。
-
计算类间散度矩阵: 类间散度矩阵S_b用于衡量不同类别之间的距离。公式为S_b = Σ(N_k * (μ_k - μ) * (μ_k - μ)^T),其中N_k表示属于第k个类别的样本数量,μ为所有样本的均值向量。
-
计算特征向量: 通过求解广义特征值问题,可以得到投影矩阵W。该矩阵的每一列对应一个特征向量,这些特征向量对应于数据在低维空间中的线性判别。具体地,我们可以选择前k个最大的特征值所对应的特征向量作为投影矩阵W。
-
降维: 将数据矩阵X乘以投影矩阵W,即可将高维数据映射到低维空间。降维后的数据矩阵Y = X * W。
通过以上步骤,我们就可以得到LDA算法的最终结果,即将高维数据映射到低维空间,并保留了最大程度的类别信息。
LDA优点
优点:
-
降维效果好:LDA通过学习类别之间的差异来选择合适的投影方向,使得同一类别样本之间的距离尽可能小,不同类别样本之间的距离尽可能大。这种特性使得LDA在降低数据维度的同时,尽可能保留了样本的类别信息。
-
解决分类问题:除了作为降维技术,LDA也可以应用于分类任务。通过选取适当的阈值,将降维后的样本进行分类。LDA在多类别分类问题上表现良好。
-
抗噪性强:LDA在处理受到一定噪声干扰的数据时,对异常值的影响相对较小。它通过学习类别之间的差异来确定投影方向,能够部分抵抗数据中的噪声。
-
简化模型:LDA可以将高维数据映射到低维空间,从而减少特征数量。这样做可以降低模型的复杂度,并且可以避免因维度灾难而导致的过拟合问题。
LDA缺点
缺点:
-
假设限制:LDA对数据的假设较为严格,例如假设数据符合正态分布、各个类别样本的协方差矩阵相等等。如果数据不满足这些假设,LDA的性能可能会下降。
-
过度拟合问题:当特征数量明显大于样本数量时,LDA的性能可能会受到影响。此时,计算类内散度矩阵的逆可能不稳定,从而导致过度拟合。
-
无法处理非线性问题:LDA是一种线性方法,只能学习线性投影来最大程度地保持类别信息。对于非线性问题,LDA的表现可能有限。
-
类别不平衡问题:当样本中某些类别的样本数量远远大于其他类别时,LDA可能会受到影响,因为它倾向于将投影方向选在样本数量较多的类别上。
基于LDA的人脸识别
机器学习之基于LDA的人脸识别_一片叶子在深大的博客-CSDN博客