一、二分查找

1.从数组中找到target的索引

 注意：while条件是<=  O（logn）

二分查找并非适用于所有情况，原因如下：

• 二分查找仅适用于有序数据。若输入数据无序，为了使用二分查找而专门进行排序，得不偿失。因为排序算法的时间复杂度通常为 \(O(n \log n)\) ，比线性查找和二分查找都更高。对于频繁插入元素的场景，为保持数组有序性，需要将元素插入到特定位置，时间复杂度为 \(O(n)\) ，也是非常昂贵的。
• 二分查找仅适用于数组。二分查找需要跳跃式（非连续地）访问元素，而在链表中执行跳跃式访问的效率较低，因此不适合应用在链表或基于链表实现的数据结构。
• 小数据量下，线性查找性能更佳。在线性查找中，每轮只需要 1 次判断操作；而在二分查找中，需要 1 次加法、1 次除法、1 ~ 3 次判断操作、1 次加法（减法），共 4 ~ 6 个单元操作；因此，当数据量 \(n\) 较小时，线性查找反而比二分查找更快。

2.二分查找边界

如果目标元素在数组中多次出现，上述介绍的方法只能保证返回其中一个目标元素的索引，而无法确定该索引的左边和右边还有多少目标元素。

如果要找到数组中第一个＝target的值的索引：

即使找到了nums[m] == target，也要让j到m-1的位置上，继续找到满足条件的更小的位置索引m。二分查找完成后，i 指向最左边的 target ，j 指向首个小于 target 的元素，因此返回索引 i 即可。

这里return的是i，如果m在第len(nums)-1的位置，那么i可能超过数组长度；以及这里并不是nums[i] == target触发return条件；所以又倒数第三行return -1的条件

 

如果要找到数组中最后一个＝target的值的索引：

 完成二分后，i指向首个大于 target 的元素，j 指向最右边的 target ，因此返回索引 j 即可。

不懂j为什么会越界？ 不加j == len(nums)是不是也可以呢？

二、哈希优化策略

我们常通过将线性查找替换为哈希查找来降低算法的时间复杂度。

目标：给定一个整数数组 nums 和一个目标元素 target ，请在数组中搜索“和”为 target 的两个元素，并返回它们的数组索引。返回任意一个解即可。

比线性搜索(O(n^2))的时间复杂度低，只需要O（n） 

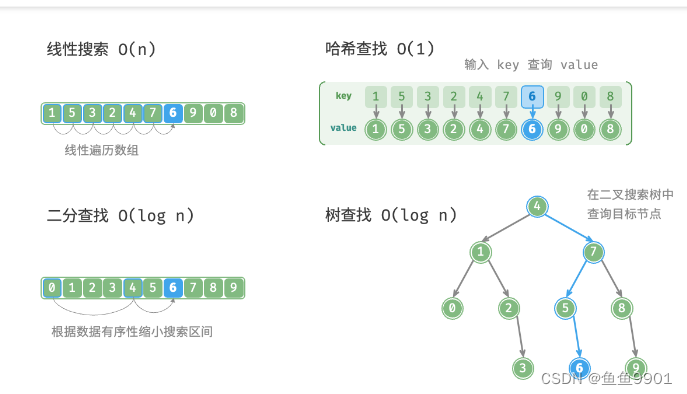
三、系统总结搜索算法

根据实现思路，搜索算法总体可分为两种：

• 通过遍历数据结构来定位目标元素，例如数组、链表、树和图的遍历等。
• 利用数据组织结构或数据包含的先验信息，实现高效元素查找，例如二分查找、哈希查找和二叉搜索树查找等。

1.暴力搜索：线性搜索（用于数组和链表等线性数据结构）；BFS、DFS（用于图和树）。O（n）

2.自适应搜索（查找算法）：利用数据的特有属性（例如有序性）来优化搜索过程，从而更高效地定位目标元素。二分查找、哈希查找、树查找。O（logn）甚至O（1）

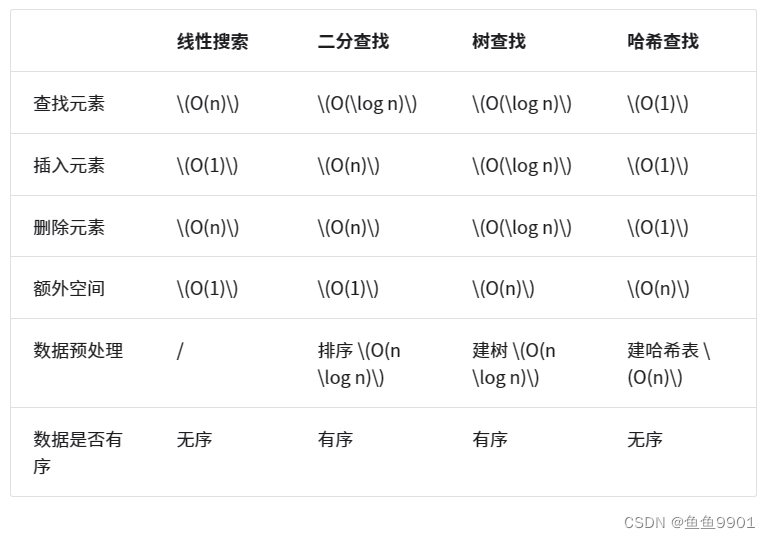
搜索方法选取：