在前一节中，我们介绍了扩展卡尔曼滤波算法EKF在目标跟踪中的应用，其原理是

将非线性函数局部线性化，舍弃高阶泰勒项，只保留一次项

，这就不可避免地会影响结果的准确性，除此以外，实际中要计算雅各比矩阵也不是特别的容易，因此有必要研究其他的滤波算法。

无迹卡尔曼滤波UKF与EKF不同，UKF不对非线性函数进行线性化，而是

仍采用传统的Kalman滤波算法框架，对于其中的一步预测方程，使用无迹变换来处理参数的非线性传递问题

由于其不是对非线性函数线性化，也无需求雅各比矩阵，因此，在精度上较EKF更加优秀。
好了，话不多少，直接开整！！！！

UKF原理

UKF滤波算法的关键之处就在于无迹变换，而所谓的无迹变换就是：

在估计点附近确定采样点，用这些样本点表示的高斯密度近似状态的概率密度函数

那么UT变换（无迹变换）具体如何实现呢，下面将进行介绍。

UT变换实现方法

无迹变换通常按以下步骤进行：

• 在原状态分布中按某一规则选取一些采样点，其中要注意：这些采样点的均值和协方差要等于原状态分布的均值和协方差；
• 将这些点代入非线性函数中，将会得到非线性函数值点集，
• 通过这些点集求取变换后的均值和协方差。

通过无迹变换，最终得到的非线性变换后的均值和协方差精度最少具有2阶精度(Taylor序列展开)，在高斯分布的条件下，精度更是可以达到三阶精度。

UT变换采样点的选择

上述提到了无迹变换需要按照一定的规则选取采样点，一般遵循以下原则：

基于先验均值和先验协方差矩阵的平方根的相关列实现的

非线性变换见的对比

我们将之前学过的EKF和今天的UKF进行对比，可见下图:

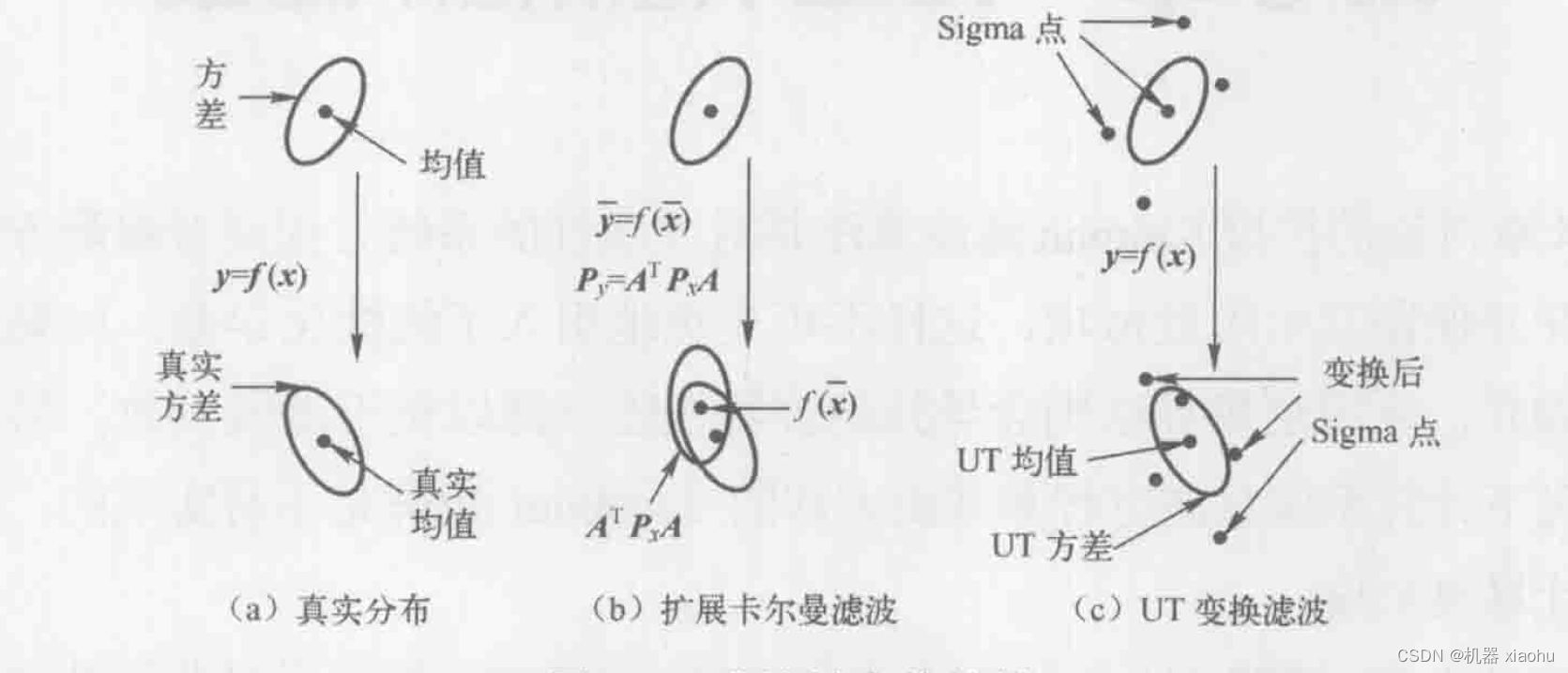
从上述的图，我们也可以看到，经过无迹变换（UT）变换后的分布，相比于EKF，更加贴近真实的分布，那么自然滤波的精度要比EKF要高一些。

UT变换的基本原理

下面我们将以对称分布采样作为例子，对于无迹变换的原理进行阐述。
此时，假设存在某非线性变换$y=f(x)$,状态向量有n维，且已知其均值$\overline{x}$和协方差P,此时就可以通过UT变换得到2n+1个Sigma点（采样点）X和相应的权值$\omega$，进而计算y的统计特性：

• 首先，计算2n+1个Sigma点，其中的n为状态量的维数，
  $$\begin{array}{rl}& X^{\left(0\right)}=\overline{X},i=0\\ & X^{(i)}=\overline{X}+{\left(\sqrt{\left(n+\lambda \right)P}\right)}_i,i=1\sim n\\ & X^{\left(i\right)}=\overline{X}-{\left(\sqrt{\left(n+\lambda \right)P}\right)}_i,i=n+1\sim 2n\end{array}$$
  上式中的${\left(\sqrt{P}\right)}^T\left(\sqrt{P}\right)=P,{\left(\sqrt{P}\right)}_i是矩阵方根的第i列$
• 然后计算这些采样点的权值，
  $$\begin{array}{rl}& {\omega }_m^{\left(0\right)}=\frac{\lambda }{n+\lambda }\\ & {\omega }_c^{(0)}=\frac{\lambda }{n+\lambda }+\left(1-a^2+\beta \right)\\ & {\omega }_m^{\left(i\right)}={\omega }_c^{\left(i\right)}=\frac{\lambda }{2\left(n+\lambda \right)},i=1\sim 2n\end{array}$$
  上述式中的下标m为均值，c为协方差，上标为第几个采样点，参数$\lambda ={\alpha }^2\left(n+k\right)-n$是一个缩放比例参数，用来降低总的预测误差，

α的选取控制了采样点的分布状态；

k为待选参数，其具体取值虽然没有界限，但通常应确保矩阵$(n+\lambda )P$为半正定矩
阵。待选参数$\beta$≥0是一个非负的权系数，它可以合并方程中高阶项的动差，这样就可以把高阶项的影响包括在内。

上述内容即使今天的全部内容了，感谢大家的观看，下次内容将进行具体的仿真验证。

如果方便，辛苦大家点个赞和关注哦！
您的点赞或评论或关注是对我最大的肯定，谢谢大家！！！

ref：卡尔曼滤波原理及应用MATLAB仿真–黄小平