目录
PCA算法
PCA目标
PCA原理推导
基于最大可分性推导
基于最近重构误差推导
PCA算法流程
PCA优点
PCA缺点
基于PCA的人脸识别
PCA算法
PCA,即主成分分析(Principal Component Analysis),是一种常用的降维技术,用于从高维数据中提取最重要的特征。
在机器学习中,我们通常面临的问题是,数据集包含大量特征,而这些特征之间可能存在冗余或相关性。这导致了两个问题:一是难以可视化和理解数据,二是可能会影响模型的性能和效率。PCA的目标就是通过线性变换将高维数据映射到低维空间,同时保持数据的主要信息。
PCA的主要应用有:
- 数据可视化:通过将高维数据投影到二维或三维空间,实现可视化展示。
- 去除冗余特征:通过降维,减少特征维度,去除冗余信息。
- 数据压缩:将数据表示为较低维度的形式,节省存储空间并加快计算速度。
- 噪声滤波:通过PCA分析噪声和信号之间的关系,减少噪声对数据的干扰。
总结一下,PCA是一种常用的降维技术,通过线性变换将高维数据映射到低维空间,保留了主要信息,同时去除了冗余和相关性。这使得数据更易于理解和分析,并可以提高机器学习模型的性能和效率。
PCA目标
最小重构误差:求重构误差最小的投影方向,即让样本点到投影超平面的距离都足够近。
最大可分性:求散度最大的投影方向,即让样本点到投影超平面的投影尽可能的分开。
PCA原理推导
基于最近重构误差和最大可分性有两种等价推导。
基于最大可分性推导



基于最近重构误差推导

即等价于最大化方差:
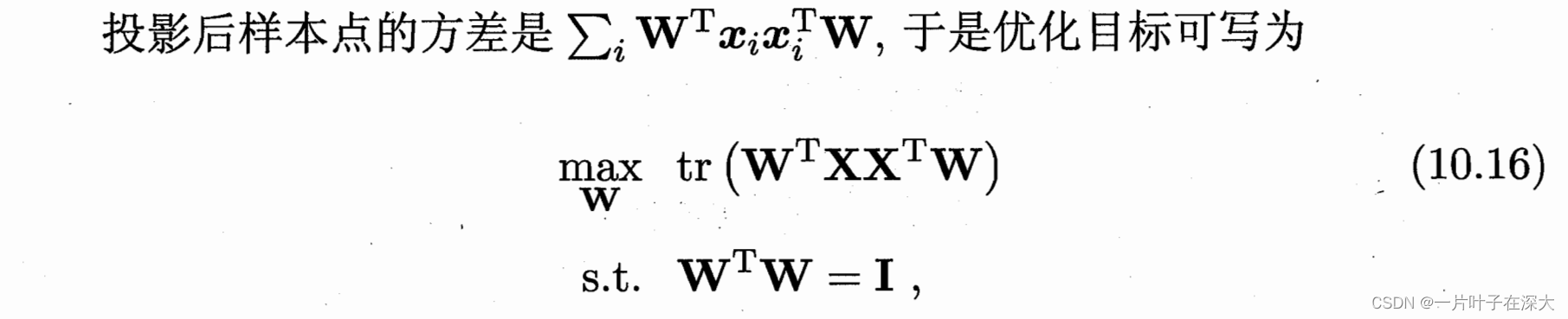
PCA算法流程
-
数据预处理:
- 标准化:对每个特征进行零均值化,即将每个特征的平均值减去整个特征列的平均值,并除以标准差。
- 可选:如果数据中存在缺失值,可以使用插补方法进行填充。
-
计算协方差矩阵:
- 协方差描述了两个变量之间的线性关系强度和方向。
- 对于一个具有n个特征的数据集,协方差矩阵是一个n×n的对称矩阵,其中每个元素表示两个特征之间的协方差。
-
特征值分解:
- 对协方差矩阵进行特征值分解,得到特征值和对应的特征向量。
- 特征向量代表了数据中的主成分,每个特征向量与一个特征值相对应。
-
特征向量选择:
- 选择最大的k个特征值对应的特征向量作为主成分,从而实现降维。
-
数据转换:
- 使用所选的k个特征向量构造转换矩阵,将原始数据映射到新的低维空间。
- 矩阵乘法操作将原始数据点映射到主成分上,得到降维后的数据。
PCA优点
PCA的优点包括:
-
降低维度:PCA可以将高维数据映射到较低维度的空间,从而减少特征的数量。这有助于去除冗余信息,提高计算效率,并且可以更好地可视化和理解数据。
-
去相关性:PCA通过线性变换将原始特征转换为一组无关的主成分。这是通过选择具有最大方差的主成分实现的,从而减少特征之间的相关性。这使得数据更易于处理和分析,提高了模型的性能和可靠性。
-
数据解释性:PCA选择的主成分对应于数据中的最大方差,因此它们包含了最重要的信息。这使得我们能够通过分析主成分来理解数据的结构和模式,以及不同特征之间的关系。
-
数据压缩:PCA将高维数据映射到较低维度,从而实现了数据的压缩。这可以减少存储空间的需求,并且在处理大规模数据时提高计算效率。
PCA缺点
PCA的缺点包括:
-
数据预处理:PCA对数据的预处理要求较高。标准化是必要的,因为PCA是基于特征之间的协方差矩阵进行计算的。如果数据不经过合适的预处理,可能会导致结果不准确或不可靠。
-
特征解释性:PCA虽然能够保留最重要的信息,但在降维的过程中也可能丢失一些较低方差的特征。这些特征可能对于特定任务的解释和理解是有意义的,但在降维过程中被忽略了。
-
非线性问题:PCA是一种线性降维方法,它假设数据是线性可分的。对于非线性问题,PCA可能无法捕捉到数据的复杂结构。针对非线性问题,可以使用核PCA或其他非线性降维方法。
-
主成分选择:确定要保留的主成分数量是一个挑战。选择较少的主成分可以实现较高的压缩率,但可能会丢失一些重要信息。而选择较多的主成分可能会保留过多的冗余信息。因此,在选择主成分的数量时需要权衡。
基于PCA的人脸识别
机器学习之基于PCA的人脸识别_一片叶子在深大的博客-CSDN博客