文章目录

说明
day69-70 矩阵分界
- 1.基于矩阵分解的推荐系统（Funk-SVD算法）
- 2.随机梯度下降（SGD）
- - 2.1 导数
  - 2.2 偏导数
  - 2.3 方向导数
  - 2.4 梯度
  - 2.5 随机梯度下降，与损失函数之间的关系
- 3.代码理解
- - 3.1 train() 方法
  - 3.2 mae方法（平均绝对误差）
  - 3.3 rsme方法（均方根误差）

说明

闵老师的文章链接：日撸 Java 三百行（总述）_minfanphd的博客-CSDN博客
自己也把手敲的代码放在了github上维护：https://github.com/fulisha-ok/sampledata

day69-70 矩阵分界

（如有问题，欢迎指正~）

1.基于矩阵分解的推荐系统（Funk-SVD算法）

基于矩阵分解的推荐系统的算法有许多，如SVD,Funk-SVD，NMF等，而结合今天的文章主要学习的是Funk-SVD算法（一种基于随机梯度下降的简化的SVD算法，通过学习用户特征和项目特征来预测评分）

基于用户-项目评分矩阵，捕捉用户和项目之间的隐含关系，通过将矩阵分解用户特征矩阵和项目特征矩阵的乘积来进行预测，如：矩阵 $m * n$ 可以分解为： $m * k 与 k * n$
例如下,假设我们特征隐含因子k就选2:

用户	电影1	电影2	电影3	电影4
user1	5	4	-	2
user2	-	2	4	-
user3	3	-	-	1
user4	-	5	2	3

我们的用户项目评分矩阵为4*4的矩阵
$\left[ \begin{array}{cc} 5 & 4& -& 2 \\ - & 2 & 4& - \\ 3 & - & -& 1 \\ - & 5 & 2& 3\\ \end{array} \right]$
我们就可以分解为U矩阵 $（ 4 * 2 ）$ 和项目矩阵 $（ 2 * 4 ）$
$\left[ \begin{array}{cc} u1-feature1 & u1-feature2 \\ u2-feature1 & u2-feature2 \\ u3-feature1 & u3-feature2 \\ u4-feature1 & u4-feature2 \\ \end{array} \right] * \left[ \begin{array}{cccc} i1-feature1 & i2-feature1 & i3-feature1 & i4-feature1 \\ i1-feature2 & i2-feature2 & i3-feature2 & i4-feature2\\ \end{array} \right]$
所以我们对原始矩阵进行分解后，假设user1对move1进行评分，那我们可以这样计算(矩阵乘法)：
$(u 1 - f e a t u re 1) * (i 1 - f e a t u re 1) + (u 1 - f e a t u re 2) * (i 1 - f e a t u re 2)$

所以呀，我们将矩阵进行分解，从中提取出用户和项目的隐藏特征，并利用这些特征进行推荐。分解为两个矩阵：用户特征矩阵表示用户在隐藏特征空间中的偏好，而项目特征矩阵表示项目在隐藏特征空间中的属性。原始矩阵： $m * n$ , 用户矩阵： $m * k$ ; 项目特征矩阵: $n * k$ （做了转置）
例如：
下面有4个用户对4部电影评分，其中满分为5分，-表示未进行评分，

用户	电影1	电影2	电影3	电影4
user1	5	4	-	2
user2	-	2	4	-
user3	3	-	-	1
user4	-	5	2	3

我们通过分解，分界为两个矩阵：用户特征矩阵和项目特征矩阵。

用户特征矩阵

用户	特征1	特征2
user1	0.8	0.6
user2	0.4	0.9
user3	0.6	0.3
user4	0.7	0.5

项目特征矩阵

项目	特征1	特征2
电影1	0.9	0.5
电影2	0.3	0.8
电影3	0.6	0.2
电影4	0.7	0.6

user1在特征1上得分较高，而user2在特征2 上得分较高。电影1在特征1上得分较高，而电影2在特征2上得分较高。现在，假设我们要向user1进行电影推荐。我们可以通过user1的特征向量与每部电影的特征向量之间进行计算来比较用户更可能喜欢那部电影，进而进行推荐。其实我们计算下来看发现我们猜用户更喜欢电影1（当然，你看我们算出评分才1.02分好像有点低所以我们还要进行不断训练来获得一个合理的分数。）
电影1: 0.80.9 + 0.6 * 0.5 = 1.02
电影2: 0.80.3 + 0.6 * 0.8 = 0.72
电影3: 0.80.6 + 0.6 * 0.2 = 0.6
电影4: 0.80.7 + 0.6 * 0.6 = 0.92

而在这个例子中，隐藏的特征值的个数如何选择？感觉是比较不好界定的，需要不断的进行调优，如果维度低了可能会丢失一些重要信息，而纬度高一些可能会增加计算复杂度和噪音等，所以需要根据具体问题和数据集的特点进行选择。
而在这个过程中，我们就会思考一个问题，这个用户矩阵和项目矩阵的特征值是怎么来的？
答：如果采用本文的算法，我们的用户特征矩阵和项目特征矩阵在最开始是赋的随机值，然后再根据随机梯度下降算法不断的去迭代更新用户和项目特征矩阵的特征值，让起预测结果更接近真实值。

2.随机梯度下降（SGD）

通过一些基础知识的回顾去理解什么是随机梯度下降，导数 -> 偏导数 -> 方向导数 -> 梯度->** 随机梯度下降**

2.1 导数

函数在这一点附近的变化率，切线的斜率，函数 $y = f (x)$ 在点 $x_{0}$ 处的导数: $\lim_{\Delta x \to 0}\frac{\Delta x}{\Delta y}=\lim_{\Delta x \to 0}\frac{f(x_{0} +\Delta x) - f(x_{0})}{\Delta x}$
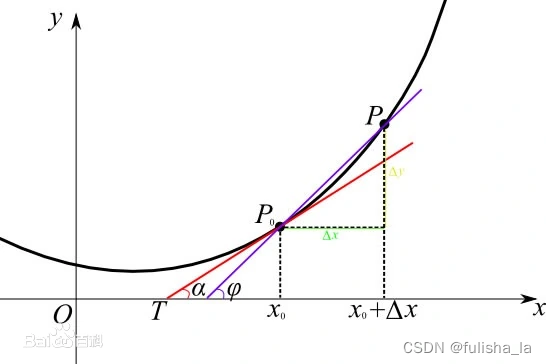
在这里插入图片描述

2.2 偏导数

一个多变量的函数的偏导数，就是它关于其中一个变量的导数而保持其他变量恒定。基于坐标轴方向的变化率
假设有二元函数 $z = f (x, y)$ ，点 $x_{0},y_{0})$ 是其定义域D 内一点。把 y 固定在 $y_{0}$ 而让 x 在 $x_{0}$ 有增量 $\Delta x$ ，相应地函数 $z = f (x, y)$ 有增量（称为对 x 的偏增量） $\Delta z=f(x_{0}+\Delta x,y_{0})-f(x_{0},y_{0})$ 函数在y方向不变，函数值沿着x轴方向的变化率
$f_{x}(x_{0}, y_{0})=\lim_{\Delta x \to 0}\frac{f(x_{0} +\Delta x, y_{0}) - f(x_{0}, y_{0})}{\Delta x}$
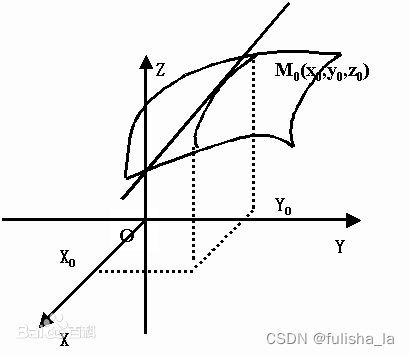
在这里插入图片描述

2.3 方向导数

在函数定义域的内点对某一方向求导得到的导数，一般为二元函数和三元函数的方向导数。方向导数可分为沿直线方向和沿曲线方向的方向导数。相比于偏导数，他能沿任意方向（函数沿着某个特定方向的变化速率） $\cos \alpha, \cos \beta$ 为L方向余弦
$\frac{\partial f}{\partial l}|(x_{0}, y_{0})=f_{x}(x_{0}, y_{0})\cos \alpha + f_{y}(x_{0}, y_{0})\cos \beta$
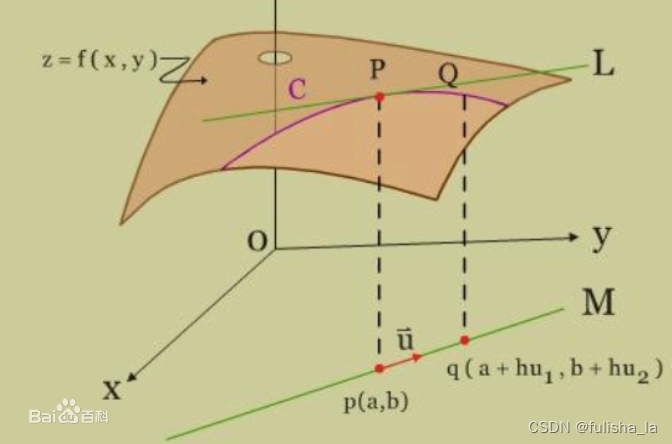
在这里插入图片描述

2.4 梯度

是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）
$gradf(x,y)=\begin{Bmatrix} \frac{\partial f}{\partial x} , \frac{\partial f}{\partial y} \end{Bmatrix}=f_{x}(x_{0},y_{0})\vec{i}+f_{y}(x_{0},y_{0})\vec{j}$

在这里插入图片描述
$\frac{\partial f}{\partial l}|(x_{0}, y_{0})=f_{x}(x_{0}, y_{0})\cos \alpha + f_{y}(x_{0}, y_{0})\cos \beta =gradf(x_{0},y_{0})\vec{e_{i}}=|gradf(x_{0}, y_{0}) |\cos\theta$

2.5 随机梯度下降，与损失函数之间的关系

在机器学习中随机梯度是指在计算梯度时，仅使用一个样本或一小批样本的数据来估计梯度。
损失函数用来衡量模型的预测输出与实际观测值之间的误差，在训练过程中我们希望最小化损失函数来使预测值接近实际值，随机梯度下降算法是优化损失函数的一种算法。文章参考

总结：

导数：函数在某点附近的变化率，是一个数值。
偏导数：函数某点沿一个某一个维度的变化率，是一个数值。
方向导数：函数某点沿一个某一个方向的变化率，是一个数值.
梯度：函数某点变化率最大的方向，是一个向量
梯度下降
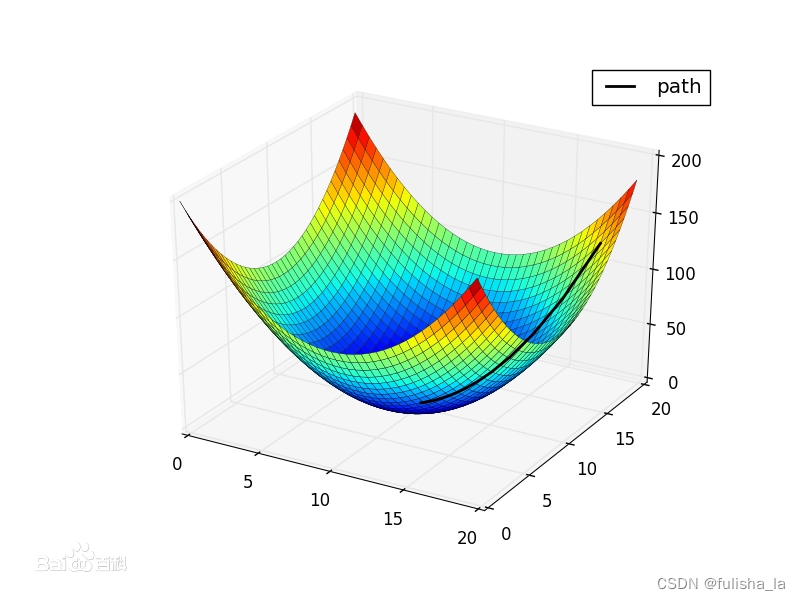
沿着梯度下降的方向求解极小值，（梯度上升：沿着梯度上升的方向可以求得极大值）梯度下降的基本思想是通过迭代的方式逐步更新模型的参数，使损失函数的值逐渐减小，最终达到局部最优或全局最优的参数值。其中随机梯度下降每次迭代只使用一个样本或一小批样本来计算梯度，并根据该梯度来更新参数（与批量梯度下降有所区别）

3.代码理解

我觉得整体的一个代码还是算比较好理解的。
从main函数出发：

 /**
     * @param args
     */
    public static void main(String args[]) {
        testTrainingTesting("C:/Users/fls/Desktop/Desktopmovielens-943u1682m (2).txt", 943, 1682, 10000, 1, 5, 2000);
    }// Of main

其中

 /**
     * Compute the MAE.
     * @return MAE of the current factorization.
     */
    public static void testTrainingTesting(String paraFilename, int paraNumUsers, int paraNumItems,
                                           int paraNumRatings, double paraRatingLowerBound, double paraRatingUpperBound,
                                           int paraRounds) {
        try {
            // Step 1. read the training and testing data
            MatrixFactorization tempMF = new MatrixFactorization(paraFilename, paraNumUsers,
                    paraNumItems, paraNumRatings, paraRatingLowerBound, paraRatingUpperBound);

            tempMF.setParameters(5, 0.0001, 0.005);

            // Step 3. update and predict
            System.out.println("Begin Training ! ! !");
            tempMF.train(paraRounds);

            double tempMAE = tempMF.mae();
            double tempRSME = tempMF.rsme();
            System.out.println("Finally, MAE = " + tempMAE + ", RSME = " + tempRSME);
        } catch (Exception e) {
            e.printStackTrace();
        }
    }

其中构造函数，setter,getter函数主要就是赋初值。

3.1 train() 方法

/**
     * Train.
     * @param paraRounds The number of rounds.
     */
    public void train(int paraRounds) {
        initializeSubspaces();

        for (int i = 0; i < paraRounds; i++) {
            updateNoRegular();
            if (i % 50 == 0) {
                // Show the process
                System.out.println("Round " + i);
                System.out.println("MAE: " + mae());
            }
        }
    }

在这个方法中主要有以下几个调用方法：

initializeSubspaces()方法

随机初始化用户矩阵和项目矩阵，而用户矩阵userSubspace和项目矩阵itemSubspace的空间大小:其中numUsers是参与评分的用户数量，numItems是参与评分的项目数量，rank就是低秩数量(隐含特征值个数，低秩的取值应小于原始矩阵的行数和列数)

userSubspace = new double[numUsers][rank];
itemSubspace = new double[numItems][rank];

迭代更新用户矩阵和物品矩阵（updateNoRegular方法）
通过随机梯度下降算法更新用户矩阵和项目矩阵使其逼近原始评分矩阵。更新的过程中，使用残差（预测评分与真实评分之间的差异）来调整梯度方向，从而逐步优化模型的拟合能力。（这里未加入正则项，）

  /**
     * Update sub-spaces using the training data.
     */
    public void updateNoRegular() {
        for (int i = 0; i < numRatings; i++) {
            int tempUserId = dataset[i].user;
            int tempItemId = dataset[i].item;
            double tempRate = dataset[i].rating;

            //残差：表示了模型对于给定数据的拟合程度，或者说模型预测与实际观测之间的偏差
            double tempResidual = tempRate - predict(tempUserId, tempItemId); // Residual

            // Update user subspace
            double tempValue = 0;
            for (int j = 0; j < rank; j++) {
                tempValue = 2 * tempResidual * itemSubspace[tempItemId][j]; // 调整梯度的方向
                userSubspace[tempUserId][j] += alpha * tempValue;
            }

            // Update item subspace
            for (int j = 0; j < rank; j++) {
                tempValue = 2 * tempResidual * userSubspace[tempUserId][j];

                itemSubspace[tempItemId][j] += alpha * tempValue;
            }
        }
    }

其中tempResidual的计算中，predict方法就是预测用户paraUser对paraItem的评分，公式就是用户矩阵和项目矩阵对应的数据相乘（内积）。

public double predict(int paraUser, int paraItem) {
        double resultValue = 0;
        for (int i = 0; i < rank; i++) {
            // The row vector of an user and the column vector of an item
            resultValue += userSubspace[paraUser][i] * itemSubspace[paraItem][i];
        }
        return resultValue;
    }

updateNoRegular方法中后面两个for循环是利用残差和学习率alpha来更新梯度方向。

3.2 mae方法（平均绝对误差）

MAE的值越小，表示预测值与真实值之间的平均差异越小，模型的预测精度越高

 public double mae() {
        double resultMae = 0;
        int tempTestCount = 0;

        for (int i = 0; i < numRatings; i++) {
            int tempUserIndex = dataset[i].user;
            int tempItemIndex = dataset[i].item;
            double tempRate = dataset[i].rating;

            double tempPrediction = predict(tempUserIndex, tempItemIndex);

            if (tempPrediction < ratingLowerBound) {
                tempPrediction = ratingLowerBound;
            }
            if (tempPrediction > ratingUpperBound) {
                tempPrediction = ratingUpperBound;
            }

            double tempError = tempRate - tempPrediction;

            resultMae += Math.abs(tempError);
            // System.out.println("resultMae: " + resultMae);
            tempTestCount++;
        }

        return (resultMae / tempTestCount);
    }

3.3 rsme方法（均方根误差）

RMSE的值越小，表示预测值与真实值之间的平均差异越小，模型的预测精度越高

 public double rsme() {
        double resultRsme = 0;
        int tempTestCount = 0;

        for (int i = 0; i < numRatings; i++) {
            int tempUserIndex = dataset[i].user;
            int tempItemIndex = dataset[i].item;
            double tempRate = dataset[i].rating;

            double tempPrediction = predict(tempUserIndex, tempItemIndex);// +
            // DataInfo.mean_rating;

            if (tempPrediction < ratingLowerBound) {
                tempPrediction = ratingLowerBound;
            } else if (tempPrediction > ratingUpperBound) {
                tempPrediction = ratingUpperBound;
            }

            double tempError = tempRate - tempPrediction;
            resultRsme += tempError * tempError;
            tempTestCount++;
        }

        return Math.sqrt(resultRsme / tempTestCount);
    }

运行结果：

Begin Training ! ! !
Round 0
MAE: 2.2907399404250066
Round 50
MAE: 0.8993292387753772
Round 100
MAE: 0.7809671561497589
Round 150
MAE: 0.7387296873184198
Round 200
MAE: 0.7170317489750806
Round 250
MAE: 0.7034448480512184
Round 300
MAE: 0.6935587511441117
Round 350
MAE: 0.6857189844613861
Round 400
MAE: 0.6789467220540055
Round 450
MAE: 0.6727002553880987
Round 500
MAE: 0.6668059407389094
Round 550
MAE: 0.6610344533820965
Round 600
MAE: 0.6552091750784605
Round 650
MAE: 0.6492148499949644
Round 700
MAE: 0.643008296616773
Round 750
MAE: 0.6365963019057151
Round 800
MAE: 0.6300215714478256
Round 850
MAE: 0.6232589520093165
Round 900
MAE: 0.6163239674271115
Round 950
MAE: 0.6093028662913618
Round 1000
MAE: 0.6022758971939184
Round 1050
MAE: 0.5953515717080884
Round 1100
MAE: 0.5885803775559597
Round 1150
MAE: 0.5819425503582748
Round 1200
MAE: 0.5755093686810299
Round 1250
MAE: 0.5692686097337987
Round 1300
MAE: 0.5632714589097246
Round 1350
MAE: 0.5574779302146219
Round 1400
MAE: 0.551919113415983
Round 1450
MAE: 0.5465747679448184
Round 1500
MAE: 0.5414617254658267
Round 1550
MAE: 0.5365844001700262
Round 1600
MAE: 0.5319456445117685
Round 1650
MAE: 0.5275238820343752
Round 1700
MAE: 0.5233039966420835
Round 1750
MAE: 0.5192706212957772
Round 1800
MAE: 0.515434234338843
Round 1850
MAE: 0.5118031247338808
Round 1900
MAE: 0.5083451638474644
Round 1950
MAE: 0.5050394579922357
Finally, MAE = 0.501970541233074, RSME = 0.661045778079508
Process finished with exit code 0