积木画

问题描述

小明最近迷上了积木画, 有这么两种类型的积木, 分别为 $I$ 型（大小为 2 个单位面积) 和 $L$ 型 (大小为 3 个单位面积):

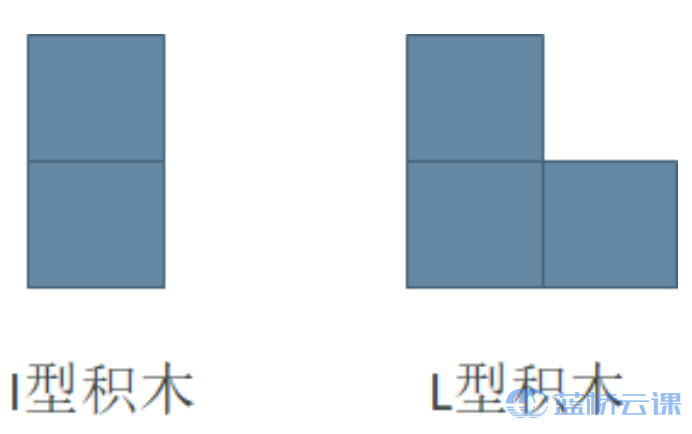
同时, 小明有一块面积大小为 $2\times N$ 的画布, 画布由 $2\times N$ 个 $1\times 1$ 区域构 成。小明需要用以上两种积木将画布拼满, 他想知道总共有多少种不同的方式? 积木可以任意旋转, 且画布的方向固定。

输入格式

输入一个整数 $N$，表示画布大小。

输出格式

输出一个整数表示答案。由于答案可能很大，所以输出其对 1000000007 取模后的值。

样例输入

3

样例输出

5

样例说明

五种情况如下图所示，颜色只是为了标识不同的积木：

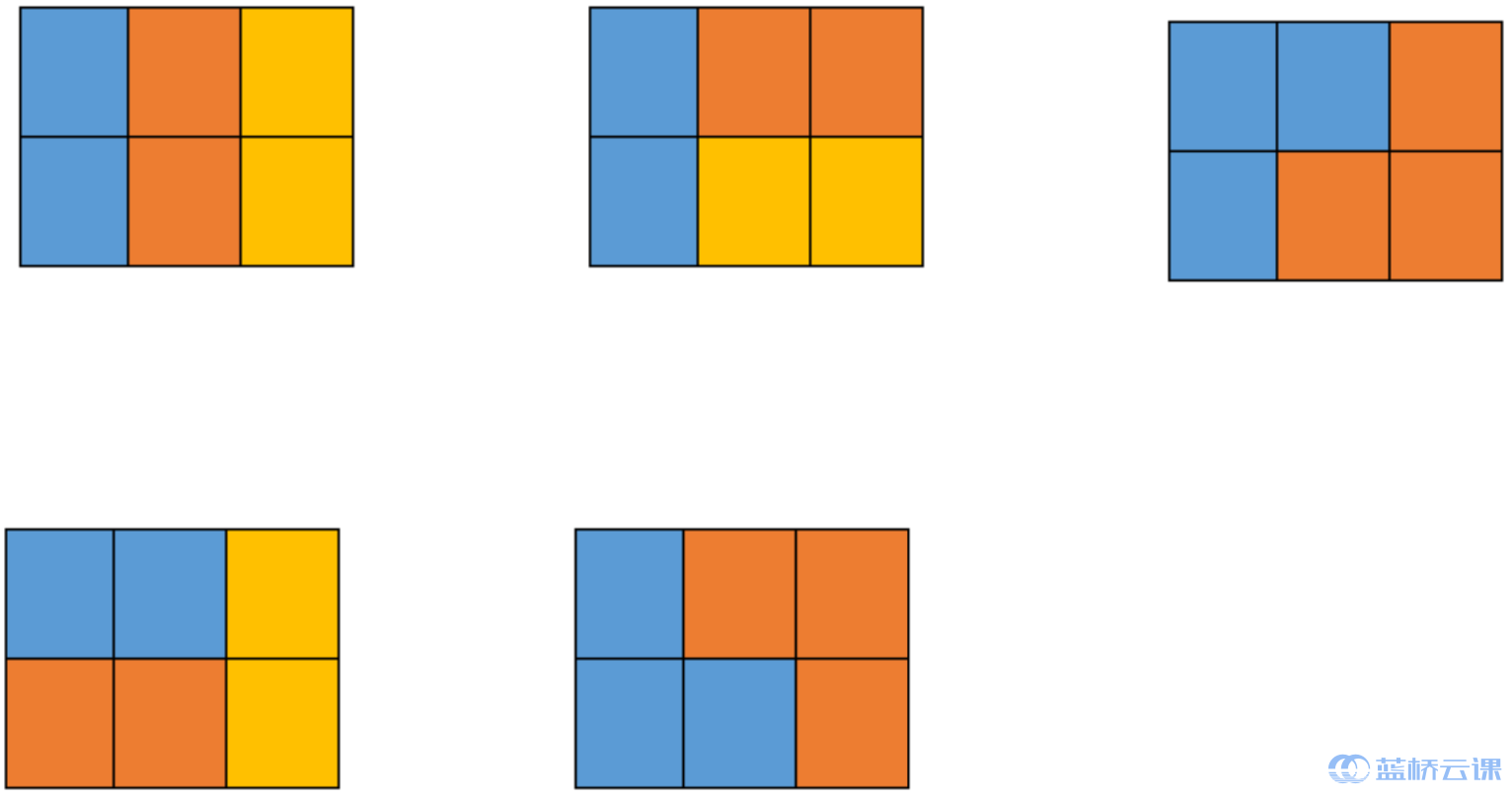
评测用例规模与约定

对于所有测试用例，$1\le N\le 10000000$.

解题思路

定义$f[n]$表示$2\times n$的画布的方案数，对于$I$型积木而言，可以很容易推断出$f[n]$与$f[n-1],f[n-2]$有关。

1. 对于$2\times (n-1)$的画布的所有方案，在最后一列放一个$I$型积木即可，也就是说$f[n]$的方案数包括$f[n-1]$的方案数。
2. 同理，对于$2\times (n-2)$的画布的所有方案，在最后两列横放两个$I$型积木即可，也就是说$f[n]$的方案数包括$f[n-2]$的方案数。
3. $L$型积木——$L$型积木只有当前$n-2$列填满，第$n-1$列只有1个单位填满时，才可以放在最后面。

这里记前$n$列填满，第$n+1$列填了一个单位时的方案数为$g[n]$。那么$f[n]$的递推式可以通过上面三种情况求得：
$$f[n]=f[n-1]+f[n-2]+g[n-2]$$
考虑$g[n]$的推导：

1. 所有的$g[n-1]$的情况后横放一个$I$型积木即可变成$g[n]$
2. 所有的$f[n-1]$的情况后可以有两种方式放置$L$型积木，可以变成$g[n]$

因此有：
$$g[n]=g[n-1]+2\ast f[n-1]$$
同时维护$g,f$，在实现时注意不断求余，防止运算溢出。

Code(Python3)(TLE)

由于 python 语言本身执行效率问题，使用相同算法的代码提交结果是超时，经过时间测试，该代码完成最大测试用例的时间在 6s 左右。

# -*- coding: utf-8 -*-
# @Author : BYW-yuwei
# @Software: python3.8.6
MOD=int(1e9+7)
maxn=int(1e7+10)

n=int(input())
f=[0]*(n+1)
g=[0]*(n+1)

f[0],f[1]=1,1
g[0],g[1]=0,2

for i in range(2,n+1):
    g[i]=(g[i-1]+2*f[i-1])%MOD
    f[i]=(f[i-1]+f[i-2]+g[i-2])%MOD
print(f[n])