题目描述

给你一个以 (radius, xCenter, yCenter) 表示的圆和一个与坐标轴平行的矩形 (x1, y1, x2, y2) ，其中 (x1, y1) 是矩形左下角的坐标，而 (x2, y2) 是右上角的坐标。

如果圆和矩形有重叠的部分，请你返回 true ，否则返回 false 。

换句话说，请你检测是否 存在 点 (xi, yi) ，它既在圆上也在矩形上（两者都包括点落在边界上的情况）。

示例1

示例2

输入：radius = 1, xCenter = 1, yCenter = 1, x1 = 1, y1 = -3, x2 = 2, y2 = -1
输出：false

示例3

提示

1 <= radius <= 2000
$-10^4<=xCenter,yCenter<=10^4$
$-10^4<=x1<x2<=10^4$
$-10^4<=y1<y2<=10^4$

思路分析

参考这一篇知乎：怎样判断平面上一个矩形和一个圆形是否有重叠？

这里提到的几点关键点我觉得很巧妙：
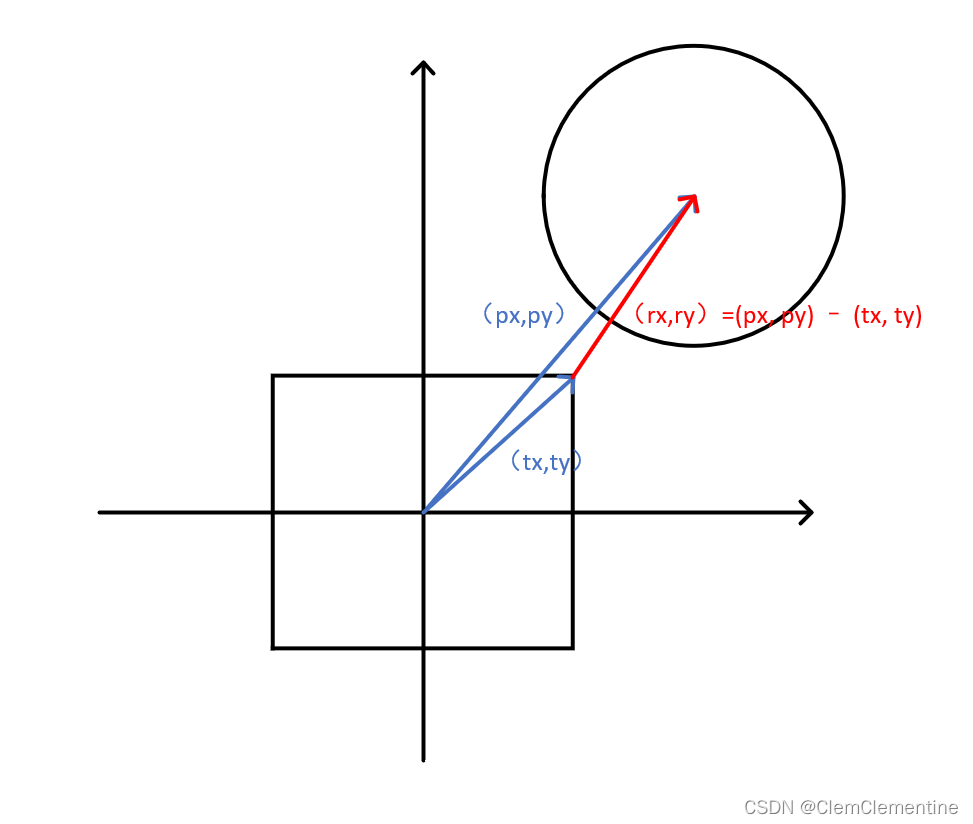
1、使用矩形中心作为中心点，而不是圆心作为中心点；如果使用圆心作为中心点，则需要考虑矩形的四个角，情况较为复杂；
2、圆心投射到第一象限具有普适性。

代码

class Solution {
public:
    //https://www.zhihu.com/question/24251545
    bool checkOverlap(int r, int x, int y, int x1, int y1, int x2, int y2) {
        // xc和yc为矩形的中心点
        double xc = 1.0 * (x1 + x2) / 2;
        double yc = 1.0 * (y1 + y2) / 2;
        //(px, py)作为从矩形中心点指向圆心的向量
        double px = abs(x - xc), py = abs(y - yc);
        //(tx, ty)作为从矩形中心到矩形右上角的向量
        double tx = x2 - xc, ty = y2 - yc;
        //(rx, ry)作为p向量和t向量的减
        double rx = px - tx, ry = py - ty;
        //根据解答描述，如果为负则置0
        if(rx < 0) rx = 0;
        if(ry < 0) ry = 0;
        if(rx * rx + ry * ry <= r * r) 
            return true;
        return false;
    }
};