图像噪声
在图像采集、处理和传输过程中会受到噪声的影响。常见的图像噪声有椒盐噪声、高斯噪声等。
椒盐噪声
椒盐噪声也叫脉冲噪声,在图像中比较常见,表现为随机出现的噪点,比如在明亮区域中出现的黑色像素。参考下图的例子:

高斯噪声
高斯噪声是指噪声密度函数服从高斯分布的一类噪声。高斯噪声也叫正态噪声,这种噪声模型经常被用于实践中。高斯随机变量z的概率密度函数如下:
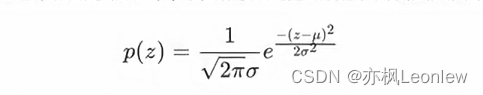
这里的z表示灰度值,表示z的平均值或期望值,
表示z的标准差。标准差的平方
为z的方差。此函数的图像如下:
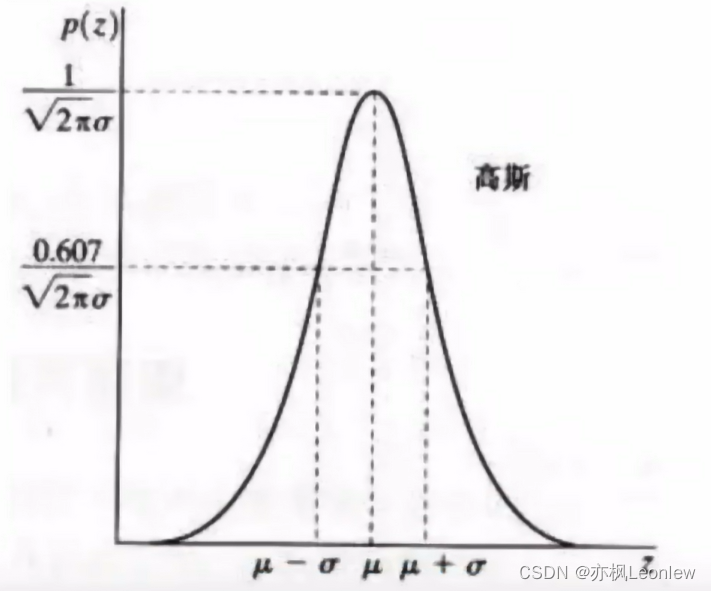
下图是高斯噪声的示例图:

图像平滑处理
图像平滑处理,从信号处理角度看就是去除其中高频信息,保留低频信息。对图像进行低通滤波可以去除图像中的噪声,对图像进行平滑处理。常见的滤波方式有:均值滤波、高斯滤波、中值滤波和双边滤波。
均值滤波
均值滤波的原理非常简单,可以理解为求平均,它使用均值滤波模板对图像噪声进行滤波。

表示中心点在(x,y),大小为m * n的矩形窗口的坐标组。
对于一个3*3的区域,均值滤波卷积框表示如下:
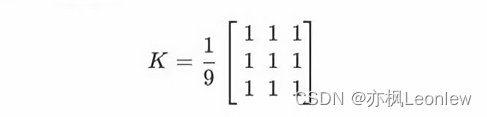
均值滤波的优点是简单,运算速度快。缺点是由于只是简单的算平均,会造成图像的细节丢失。下图为使用均值滤波降噪后的对比图:

高斯滤波
二维高斯分布函数
由于图像有两个维度(x和y),因此二维高斯分布函数是构建高斯滤波的基础。

二维高斯分布函数的图像如下:
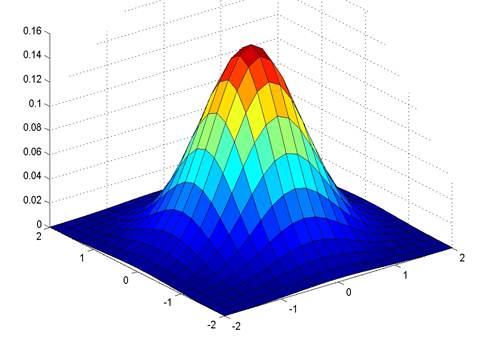
关于高斯分布图像的更多细节,可参考这里:
多维高斯分布---【2】_二维高斯分布_王延凯的博客的博客-CSDN博客多维高斯分布1.一维高斯分布2.二维高斯分布3.多维高斯分布4.心声1.一维高斯分布\qquad在介绍二维高斯分布之前我们先介绍一下一维高斯分布的函数图像,如下所示:f(x)=12π⋅δ⋅e−(x−μ)22δ2f(x)= \frac{1}{\sqrt{2 \pi}\cdot \delta}\cdot e^{-\frac{{(x-\mu)}^2}{2\delta^2}}f(x)=2π⋅δ...https://blog.csdn.net/weixin_38468077/article/details/103508072 这里的
可以看做两个值,x方向的标准差
以及y方向的标准差
。
和
取值越大,整个形状就越扁平;反之则形状越尖。高斯分布是一种钟形曲线,越靠近中心位置,值就越大;离中心越远值越小。在使用高斯滤波时,将“中心点”作为原点,其他点按照其在高斯分布曲线上的位置分配权重,最终通过卷积得到一个加权平均值。
高斯滤波过程
1. 确定权重矩阵
假设图像中心点坐标为(0,0),则和中心点相邻的8个点坐标(3x3窗口为例)为:

要计算权重矩阵,首先要设定,我们假设它是1.5。然后代入x和y的坐标值计算出权重模板:

这9个点的权重和等于0.4787147,并不等于1,为了让所有权重的和等于1,我们对这9个值分别除以0.4787147,这样就得到了最终的权重矩阵(按照各个像素权重百分比表示)。
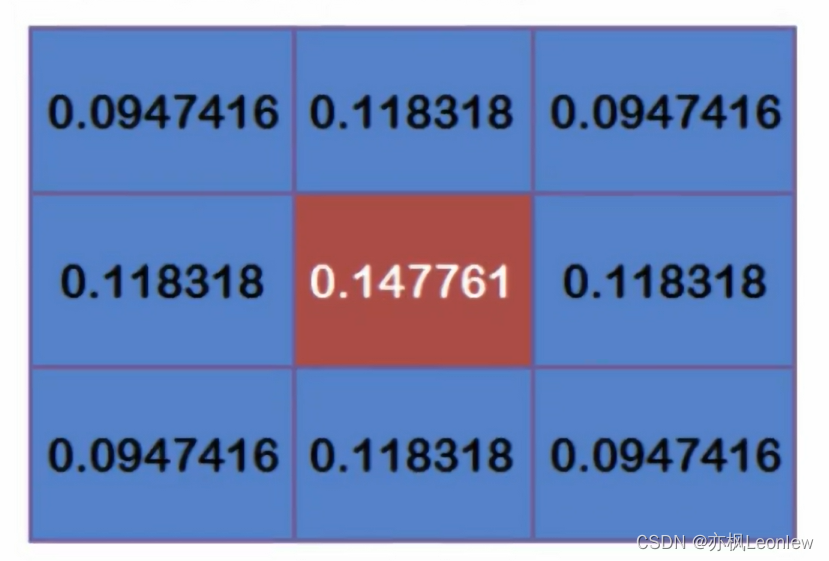
得到权重矩阵后,就可以对图像进行卷积做高斯滤波了。
假设有一个3x3的像素矩阵,9个像素点的值如下:
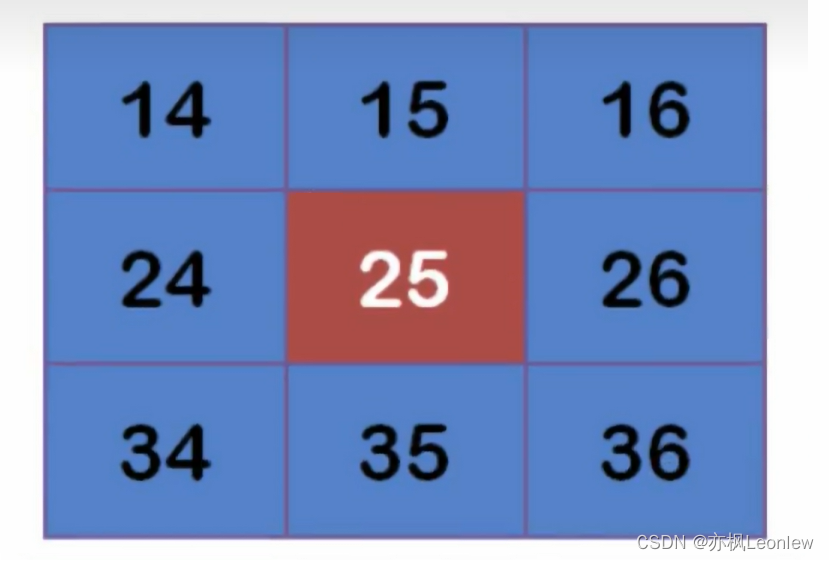
对每个点都乘以权重矩阵中对应位置的值,得到的结果如下:

最后,中心点像素的值就是9个点像素值的和:
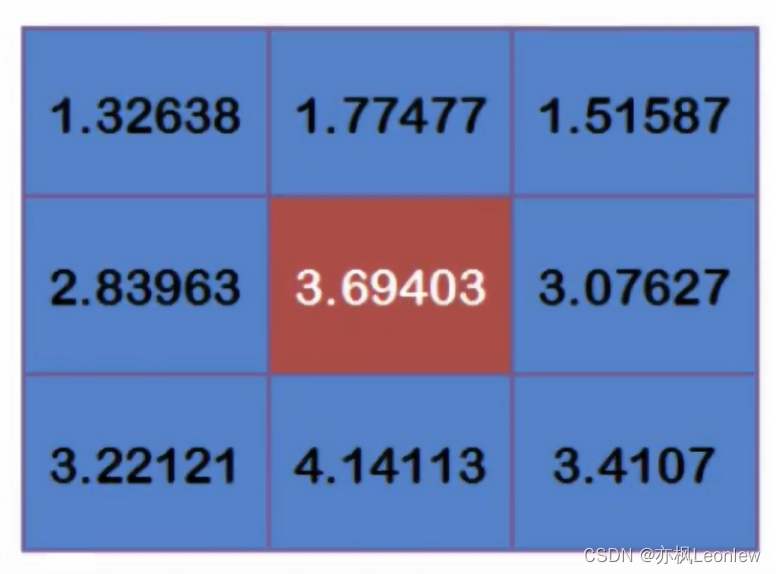
对于RGB图像,只要对三个通道分别进行高斯模糊就可以得到对应的像素值。
高斯滤波的效果的例子如下:

中值滤波
中值滤波原理非常简单,中值就是中间值,这种滤波方法对于滤除椒盐噪声效果非常好。具体做法是对窗口内的像素值进行排序,找到中间值后,用中间值作为像素点的值。
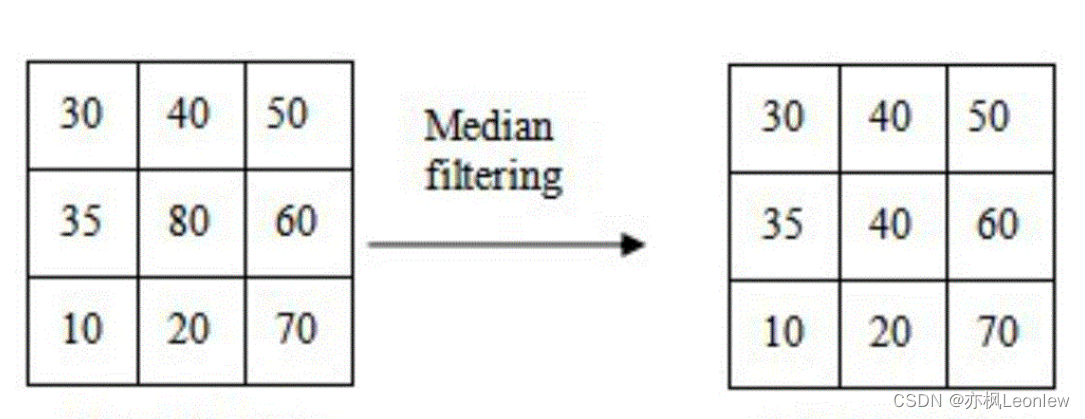
上图左侧的3x3窗口中,按照像素值大小排序可得:10,20,30,35,40,50,60,70,80。可以得到中间值为40,因此像素中心点的值在中值滤波后会变成40。