---

回归模型评价方法

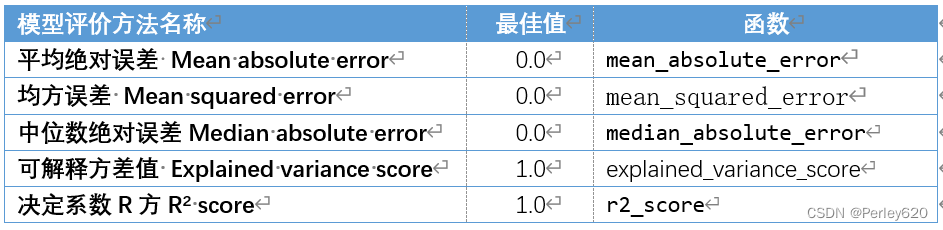
from sklearn.metrics import explained_variance_score,\
mean_absolute_error,\
mean_squared_error,\
median_absolute_error,r2_score
print('Boston数据线性回归模型的平均绝对误差为：',
     mean_absolute_error(y_test,y_pred))
print('Boston数据线性回归模型的均方误差为：',
     mean_squared_error(y_test,y_pred))
print('Boston数据线性回归模型的中值绝对误差为：',
     median_absolute_error(y_test,y_pred))
print('Boston数据线性回归模型的可解释方差值为：',
     explained_variance_score(y_test,y_pred))
print('Boston数据线性回归模型的R方值为：',
     r2_score(y_test,y_pred))

【回归】线性回归模型

1.线性模型

2.线性回归

定义：线性回归通过一个或者多个自变量与因变量之间之间进行建模的回归分析。其中特点为一个或多个称为回归系数的模型参数的线性组合

3.损失函数（误差大小）

4.解决方法

1) 最小二乘法之正规方程

2) 最小二乘法之梯度下降

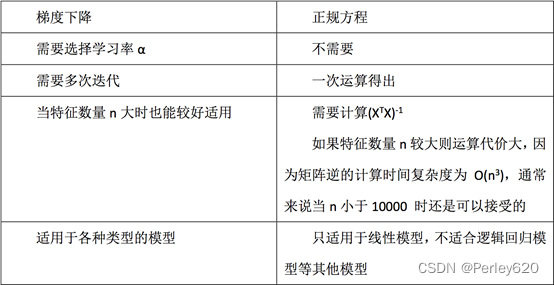
5.代码实现

正规方程：

sklearn.linear_model.LinearRegression()

梯度下降：

sklearn.linear_model.SGDRegressor()

5+.模型保存与加载

from sklearn.externals import joblib
# 保存训练好的模型
joblib.dump(lr, "./test.pkl")
# # 预测房价结果
model = joblib.load("./test.pkl")
y_predict = std_y.inverse_transform(model.predict(x_test))
print("保存的模型预测的结果：", y_predict)

6.特点

特点：线性回归器是最为简单、易用的回归模型。

• 从某种程度上限制了使用，尽管如此，在不知道特征之间关系的前提下，我们仍然使用线性回归器作为大多数系统的首要选择。

• 小规模数据：LinearRegression(不能解决拟合问题)以及其它大规模数据：SGDRegressor

实例：波士顿房价

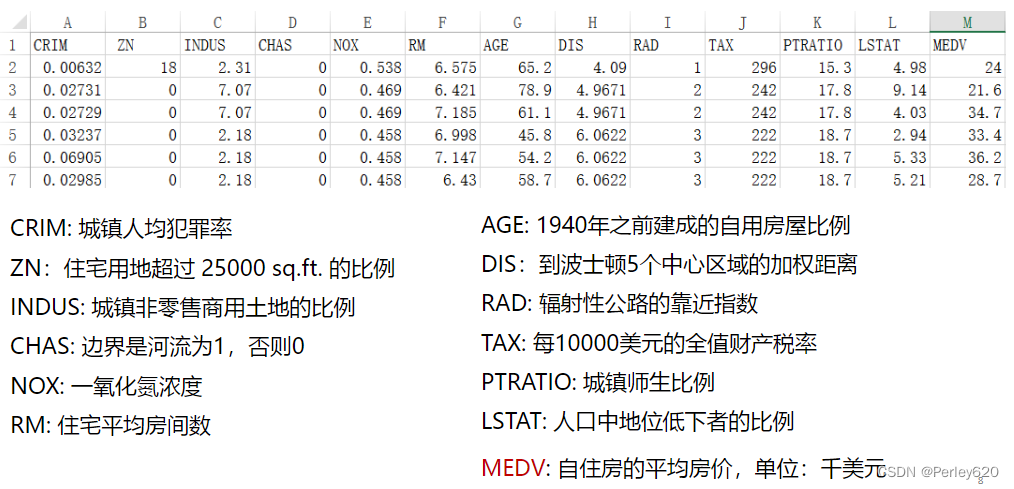
模型训练：

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression,SGDClassifier
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, classification_report
import numpy as np
def myliner():
    '''
    线性回归直接预测房子价格
    :return:None
    '''
    #分隔数据集
    lb=load_boston()
    x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
    # print(x_train,x_test)
    #标准化处理
    # 特征工程（标准化）
    std = StandardScaler()
    # 对测试集和训练集的特征值进行标准化
    # 目标值也需要标准化处理！！！！实例化两个标准化API
    std_x = StandardScaler()
    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)
    #目标值
    std_y = StandardScaler()
    y_train = std_y.fit_transform(y_train.reshape(-1,1))#要求数据是二维数据
    y_test = std_y.transform(y_test.reshape(-1,1))
    ###########################################
    # 正规方程
    lr = LinearRegression()
    lr.fit(x_train, y_train)
    print("正规方程的回归系数",lr.coef_)#得到的回归系数
    # 保存训练好的模型
    from sklearn.externals import joblib
    joblib.dump(lr, "./test.pkl")
    # 预测测试集的房子价格#逆操作，逆标准化
    y_lr_predict = std_y.inverse_transform(lr.predict(x_test))    # print("正规方程测试集里面每个房子的预测价格：", y_lr_predict)
    print("正规方程的均方误差：", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))
    ###############################
    # # #梯度下降
    std_x1 = StandardScaler()
    x_train1 = std_x1.fit_transform(x_train)
    x_test1 = std_x1.transform(x_test)
    # 目标值
    std_y1 = StandardScaler()
    y_train1 = std_y1.fit_transform(y_train.reshape(-1, 1))  # 要求数据是二维数据
    y_test1 = std_y1.transform(y_test.reshape(-1, 1))
    y_train = y_train1.astype("int")
    x_train = x_train1.astype("int")
    sgd = SGDClassifier()
    sgd.fit(x_train, y_train)
    print("梯度下降得到的回归系数",sgd.coef_)  # 得到的回归系数
    # 保存训练好的模型
    from sklearn.externals import joblib
    joblib.dump(sgd, "./test.pkl")
    # 预测测试集的房子价格
    # y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))  # 逆操作，逆标准化
    # print("梯度下降测试集里面每个房子的预测价格：", y_sgd_predict)
    # print("梯度下降的均方误差：", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))
if __name__ == '__main__':
    myliner()

进行预测

from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
## 加载boston数据
boston = load_boston()
X = boston['data']
y = boston['target']
names = boston['feature_names']
## 将数据划分为训练集测试集
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.2,random_state=125)
## 建立线性回归模型
clf = LinearRegression().fit(X_train,y_train)
print('建立的LinearRegression模型为：','\n',clf)
## 预测训练集结果
y_pred = clf.predict(X_test)
print('预测前20个结果为：','\n',y_pred[:20])
# 代码 6-25
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.sans-serif'] = 'SimHei'
fig = plt.figure(figsize=(10,6)) ##设定空白画布，并制定大小
##用不同的颜色表示不同数据
plt.plot(range(y_test.shape[0]),y_test,color="blue", linewidth=1.5, linestyle="-")
plt.plot(range(y_test.shape[0]),y_pred,color="red", linewidth=1.5, linestyle="-.")
plt.legend(['真实值','预测值'])
#plt.savefig('../tmp/聚类结果.png')
plt.show() ##显示图片

【回归】带有L2正则化的岭回归

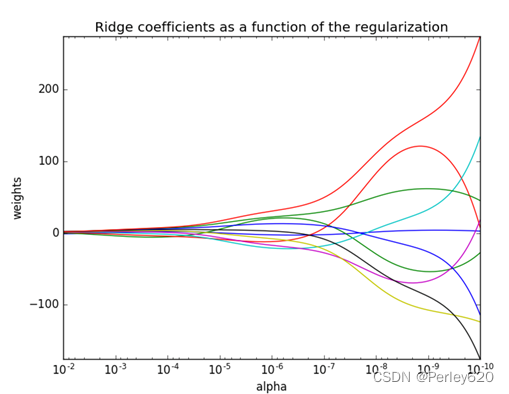正则化系数越大，权重趋近于0，模型越来越简单。

线性回归 LinearRegression与Ridge对比

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor,  Ridge, LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, classification_report
from sklearn.externals import joblib
import pandas as pd
import numpy as np
def rd():
    """
    线性回归直接预测房子价格
    :return: None
    """
    # 获取数据
    lb = load_boston()
    # 分割数据集到训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
    print(y_train, y_test)
    # 进行标准化处理(?) 目标值处理？
    # 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
    std_x = StandardScaler()
    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)
    # 目标值
    std_y = StandardScaler()
    y_train = std_y.fit_transform(y_train.reshape(-1, 1))
    y_test = std_y.transform(y_test.reshape(-1, 1))
    # # 预测房价结果
    # model = joblib.load("./tmp/test.pkl")
    # y_predict = std_y.inverse_transform(model.predict(x_test))
    # print("保存的模型预测的结果：", y_predict)
    # # estimator预测
    # 正规方程求解方式预测结果
    lr = LinearRegression()
    lr.fit(x_train, y_train)
    print(lr.coef_)
    # 保存训练好的模型
    # joblib.dump(lr, "./tmp/test.pkl")
    # 预测测试集的房子价格
    y_lr_predict = std_y.inverse_transform(lr.predict(x_test))
    print("正规方程测试集里面每个房子的预测价格：", y_lr_predict)
    print("正规方程的均方误差：", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))
    # 梯度下降去进行房价预测
    sgd = SGDRegressor()
    sgd.fit(x_train, y_train)
    print(sgd.coef_)
    # 预测测试集的房子价格
    y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))
    print("梯度下降测试集里面每个房子的预测价格：", y_sgd_predict)
    print("梯度下降的均方误差：", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))
    # 岭回归去进行房价预测
    rd = Ridge(alpha=1.0)
    rd.fit(x_train, y_train)
    print(rd.coef_)
    # 预测测试集的房子价格
    y_rd_predict = std_y.inverse_transform(rd.predict(x_test))
    print("岭回归测试集里面每个房子的预测价格：", y_rd_predict)
    print("岭回归的均方误差：", mean_squared_error(std_y.inverse_transform(y_test), y_rd_predict))
    return None
if __name__ == '__main__':
    rd()