本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:https://github.com/timerring/information-theory 】或者公众号【AIShareLab】回复 信息论 获取。
文章目录
- 伪随机码
- 伪随机序列的概念
- 伪随机序列的产生
伪随机码
伪随机序列的概念
伪随机序列应当具有类似随机序列的性质。在工程上常用二元 {0,1} 序列来产生伪随机(噪声)码, 它具有以下几个特点:
- 在随机序列的每一个周期内 0 和 1 出现的次数近似相等。
- 每一周期内, 长度为 n \boldsymbol{n} n 的游程取值(相同码元的码元串)出现的次数比长度为 n+1 的游程次数多一倍。
- 随机序列的自相关类似于白噪声自相关函数的性质。
对伪随机码定义可写为
(1)凡自相关函数具有
ρ x ( j ) = { ∑ i = 1 n x i 2 p = 1 , j = 0 ∑ i = 1 n x i x i + j p = − 1 p , j ≠ 0 . \rho_{x}(j)=\{\begin{array}{l} \sum_{i=1}^{n} \frac{x_{i}^{2}}{p}=1, \quad j=0 \\ \sum_{i=1}^{n} \frac{x_{i} x_{i+j}}{p}=-\frac{1}{p}, j \neq 0 \end{array}. ρx(j)={∑i=1npxi2=1,j=0∑i=1npxixi+j=−p1,j=0.
形式的码, 称为伪随机码, 又称为狭义伪随机码。
(2) 凡自相关函数具有
ρ x ( j ) = { ∑ i = 1 n x i 2 / p = 1 j = 0 ∑ i = 1 n x i x i + j / p = a < 1 j ≠ 0 . \rho_{x}(j)=\{\begin{array}{ll} \sum_{i=1}^{n} x_{i}^{2} / p=1 & j=0 \\ \sum_{i=1}^{n} x_{i} x_{i+j} / p=a<1 & j \neq 0 \end{array}. ρx(j)={∑i=1nxi2/p=1∑i=1nxixi+j/p=a<1j=0j=0.
形式的码, 称为广义伪随机码。狭义伪随机码是广义伪随机码的特例。
伪随机序列的产生
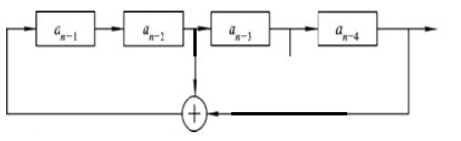
可以用移位奇存器作为伪随机码产生器, 图1是一个4级移位寄存 器, 用它就可产生伪随机序列。图1中的反馈逻辑为
a
n
=
a
n
−
3
⊕
a
n
−
4
a_{n}=a_{n-3} \oplus a_{n-4}
an=an−3⊕an−4
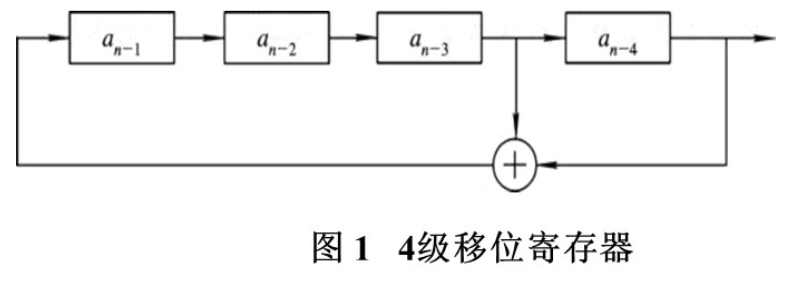
当移位寄存器的初始状态是 a n − 4 = 1 a_{n-4}=1 an−4=1, a n − 3 = 0 a_{n-3}=0 an−3=0, a n − 2 = 0 a_{n-2}=0 an−2=0, a n − 1 = 0 a_{n-1}=0 an−1=0 , 经过一 个时钟节拍后, 各级状态自左向右移到下一级, 末级输出一位数, 与此同时模二加法器输出加到移位寄存器第一级, 从而形成移位 寄存器的新状态, 下一个时钟节拍到来又继续上述过程, 末级输出序列就是伪随机序列。在这种条件下, 产生的伪随机序列是

这是一个周期长度p=15的伪随机序列。
当上图的初始状态是 0 状态时, 即 a n − 4 = a n − 3 = a n − 2 = a n − 1 = 0 a_{n-4}=a_{n-3}=a_{n-2}=a_{n-1}=0 an−4=an−3=an−2=an−1=0 移存器的输 出是一个0序列。
4 级移存器共有 16 个状态, 除去一个 0 状态外, 还有 15 个状态。 对于图1来说, 只要随机序列的周期达到最大值, 这时无论如何 改变移存器的初始状态, 其输出只改变序列的初相, 序列的排 序规律不会改变。
但如果改变图四级移存器的反馈逻辑, 其输出序列就会发生变化。
下图中的反馈逻辑是 a n = a n − 2 ⊕ a n − 4 a_{n}=a_{n-2} \oplus a_{n-4} an=an−2⊕an−4 , 初始状态为 1111, 输出序列为111100111100111…
反馈逻辑是 a n = a n − 2 ⊕ a n − 4 a_{n}=a_{n-2} \oplus a_{n-4} an=an−2⊕an−4 , 时, 给定不同的初始状态1111、 0001 、 1011 , 可以得到三个完全不同的输出序列 111100111100…, 000101000101…,101101101101。它们的周期分别是6、6和3。
由此, 我们可以得出以下几点结论:
(1)线性移位寄存器的输出序列是一个周期序列。
(2)当初始状态是0状态时, 线性移位寄存器的输出是一个0序列。
(3)级数相同的线性移位寄存器的输出序列与寄存器的反馈逻辑有关。
(4)序列周期 p < < 2 n − 1 p^{<}<\mathbf{2}^{n}-1 p<<2n−1 (n级线性移位寄存器) 的同一个线性移存器的输 出还与起始状态有关。
(5) 序列周期 p n = 2 n − 1 p^{n}=2^{n}-1 pn=2n−1 的线性移位寄存器, 改变移位寄存起初始状态 只改变序列的起始相位, 而周期序列排序规律不变。
参考文献:
- Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- 周炯槃. 通信原理(第3版)[M]. 北京:北京邮电大学出版社, 2008.
- 樊昌信, 曹丽娜. 通信原理(第7版) [M]. 北京:国防工业出版社, 2012.