一、基本原理
在信息论中,熵是对不确定性的一种度量。不确定性越大,熵就越大,包含的信息量越大;不确定性越小,熵就越小,包含的信息量就越小。
根据熵的特性,可以通过计算熵值来判断一个事件的随机性及无序程度,也可以用熵值来判断某个指标的离散程度,指标的离散程度越大,该指标对综合评价的影响(权重)越大。
样本数据在某指标下取值都相等,则该指标对总体评价的影响(贡献)为0,故其权重也应该为0.
熵权法是一种客观赋权法,因为它仅依赖于数据本身的离散性。
二、熵权法步骤
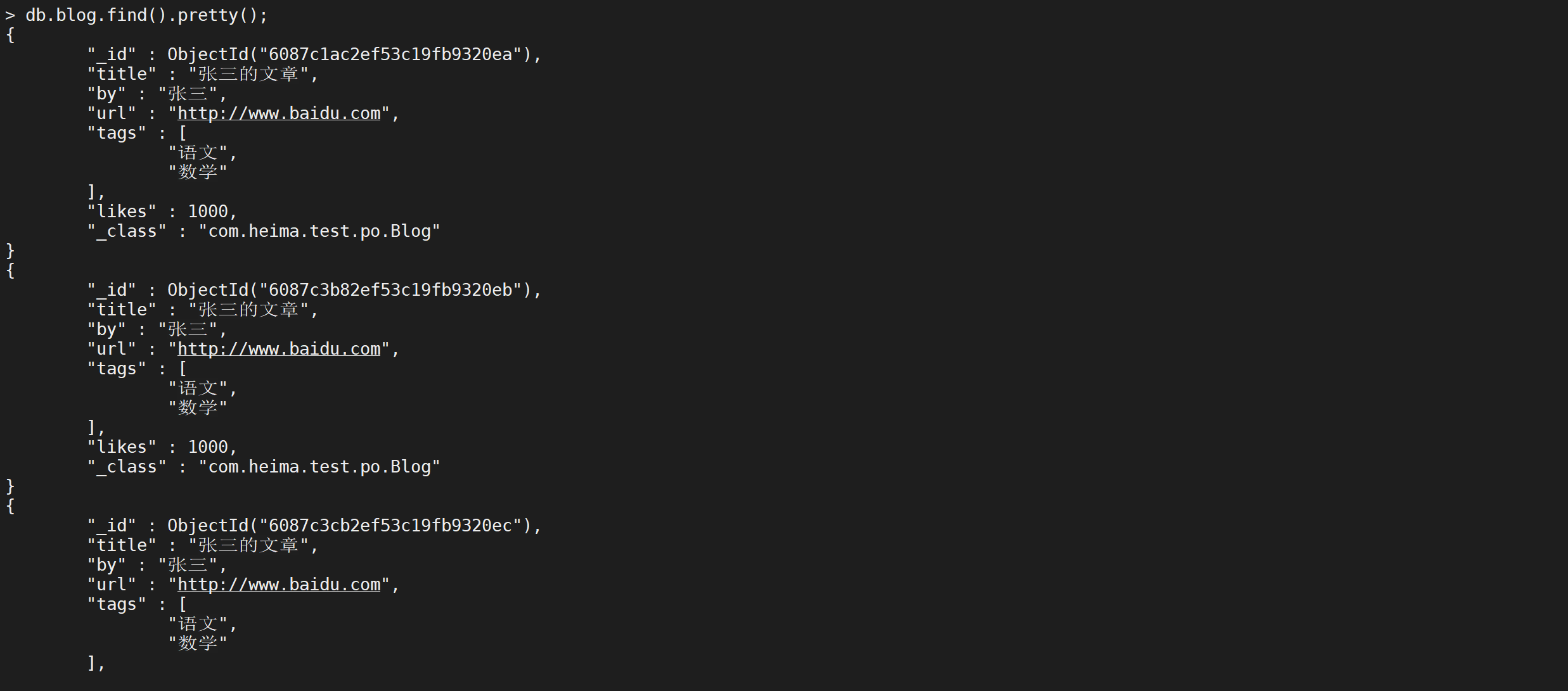
1.对n个样本,m个指标,则xij为第i个样本的第j个指标的数值(i=1,2...,n;j=1,2,...,m)
2. 指标的归一化处理:异质指标同质化
由于各项指标的计量单位并不统一,因此在用它们计算综合指标前,先要进行标准化处理,即把指标的绝对值转化为相对值,从而解决各项不同质指标值的同质化问题。
另外,正向指标和负向指标数值代表的含义不同(正向指标数值越高越好,负向指标数值越低越好),因此,对于正向负向指标需要采用不同的算法进行数据标准化处理:
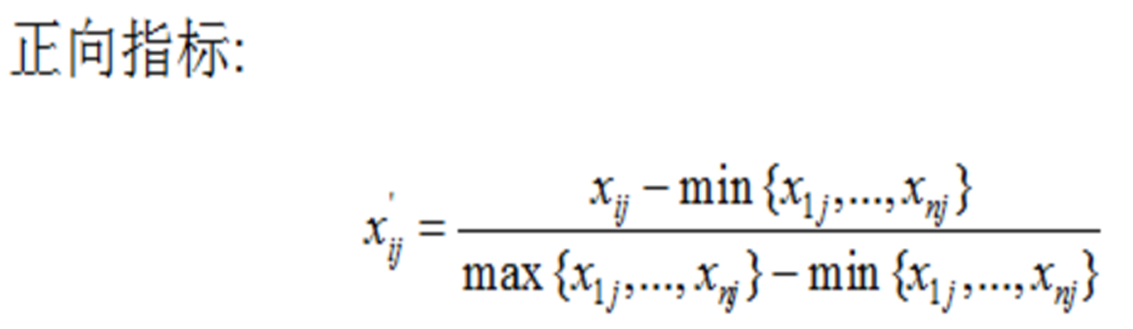
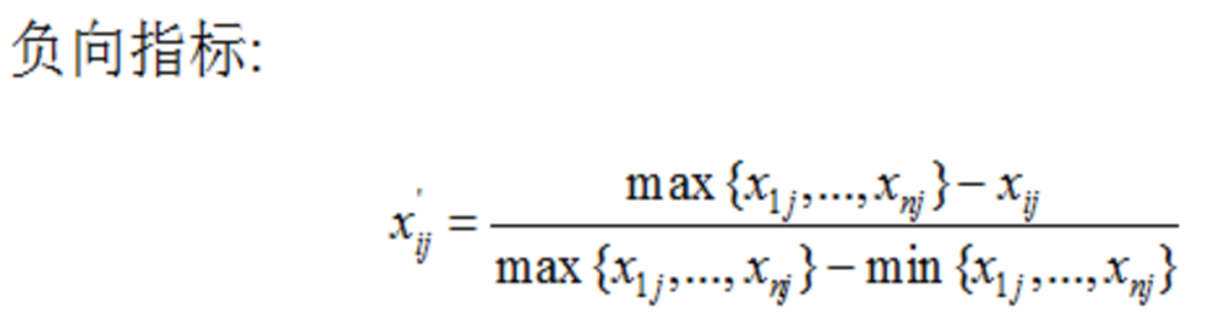
这里就是之前说的极差变换法


例:某物流公司为了提高自身的服务水平,对拥有的11个部门进行了考核,考核标准包括9项,并对服务水平较好的部门进行奖励。下表是对各个部门指标考核后的评分结果。
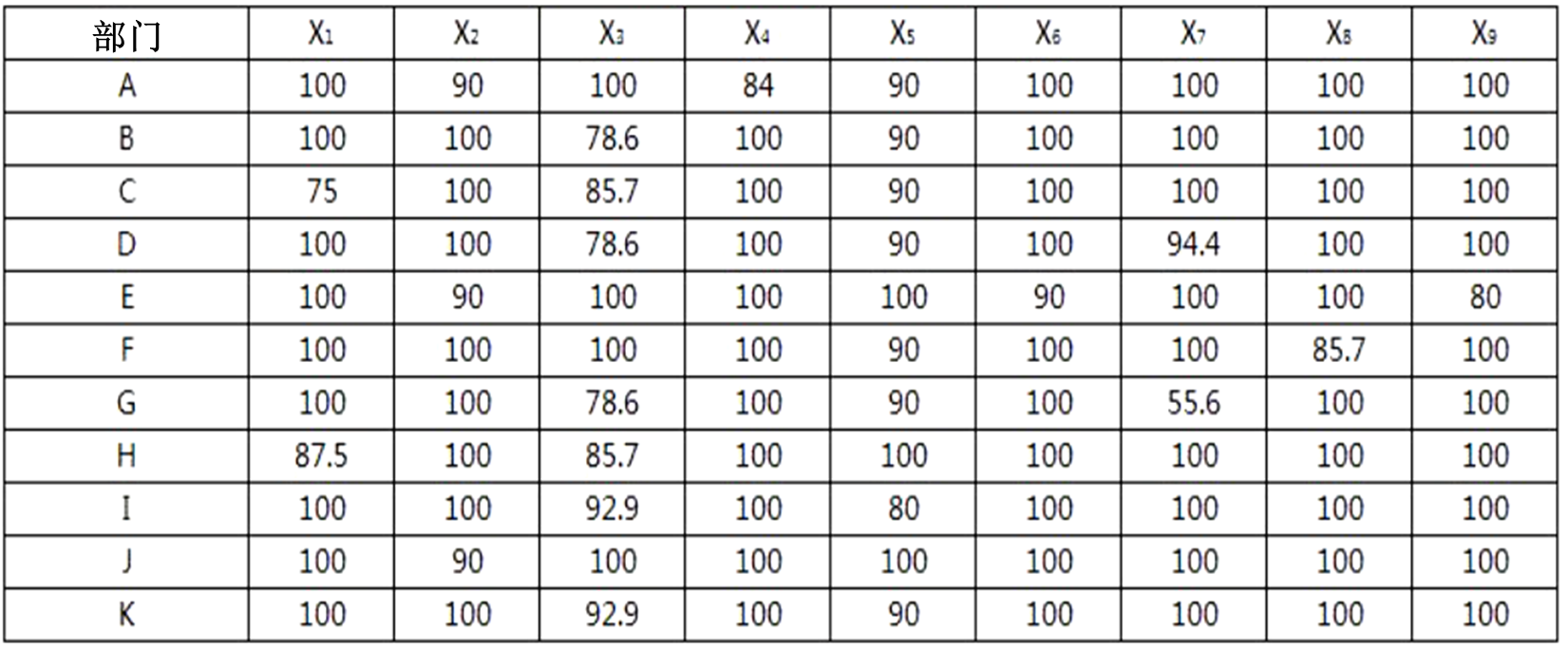
1. 熵权法进行赋权
1)数据标准化
根据原始评分表,对数据进行标准化后可以得到下列数据标准化表

2)计算Pij

3)计算各指标熵值



4)计算各指标权重
| 熵值 | 0.95 | 0.87 | 0.84 | 0.96 | 0.94 | 0.96 | 0.96 | 0.96 | 0.96 | |
| 冗余度 | 0.05 | 0.13 | 0.16 | 0.04 | 0.06 | 0.04 | 0.04 | 0.04 | 0.04 | 0.6 |
| 权重 | 0.08 | 0.22 | 0.27 | 0.07 | 0.10 | 0.07 | 0.07 | 0.07 | 0.07 | 1.00 |
 最后计算各部门得分
最后计算各部门得分
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | 得分 | |
| A | 1 | 0 | 1 | 0 | 0.5 | 1 | 1 | 1 | 1 | 0.69 |
| B | 1 | 1 | 0 | 1 | 0.5 | 1 | 1 | 1 | 1 | 0.71 |
| C | 0 | 1 | 0.33 | 1 | 0.5 | 1 | 1 | 1 | 1 | 0.71 |
| D | 1 | 1 | 0 | 1 | 0.5 | 1 | 0.87 | 1 | 1 | 0.70 |
| E | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0.67 |
| F | 1 | 1 | 1 | 1 | 0.5 | 1 | 1 | 0 | 1 | 0.91 |
| G | 1 | 1 | 0 | 1 | 0.5 | 1 | 0 | 1 | 1 | 0.64 |
| H | 0.5 | 1 | 0.33 | 1 | 1 | 1 | 1 | 1 | 1 | 0.81 |
| I | 1 | 1 | 0.67 | 1 | 0 | 1 | 1 | 1 | 1 | 0.83 |
| J | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.81 |
| K | 1 | 1 | 0.67 | 1 | 0.5 | 1 | 1 | 1 | 1 | 0.89 |
| 权重 | 0.08 | 0.22 | 0.27 | 0.07 | 0.11 | 0.07 | 0.07 | 0.07 | 0.07 | 8.35 |