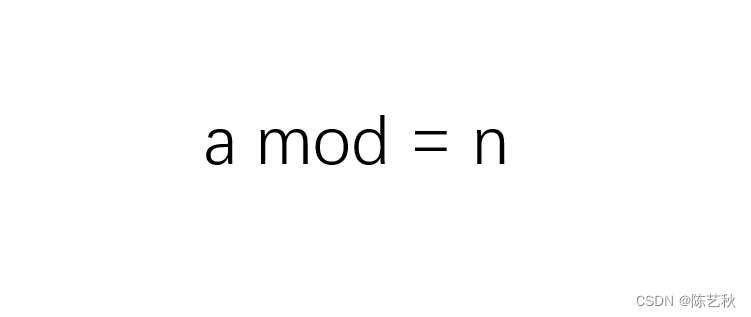数学很酷！使用RSA算法对秘密消息进行解码，c，p，q，e是RSA算法的参数。

RSA算法还不太了解，经过这段时间的学习，得知

• q和p是最开始选择的两个质数，主要是为了计算出钥匙n

• e是在1到φ(n)之间选择的一个数字，与φ(n)互质

• c则是密文，这道题的要求就是计算出解密的密钥（n，d）然后带入m = c^d % n，得出原文

解题步骤

数据这么老长，自己计算掉得把我送走，所以还是编写脚本来计算吧

经过查看wp，得知了一个新的Python库，gmpy2

1. 首先我们计算出q和p两个质数的乘积n

2. 再根据欧拉函数，求出φ(n）的值：也就是(p-1)(q-1)

3. 根据e求φ(n）的模反元素d，也就是逆元：ed ≡ 1 (mod φ(n))

1. 通俗的说就是e乘以多少再向φ(n)取余等于1

4. 求出d的值后与n进行组合就可以得到私钥的值，最终结果m = c^d % n

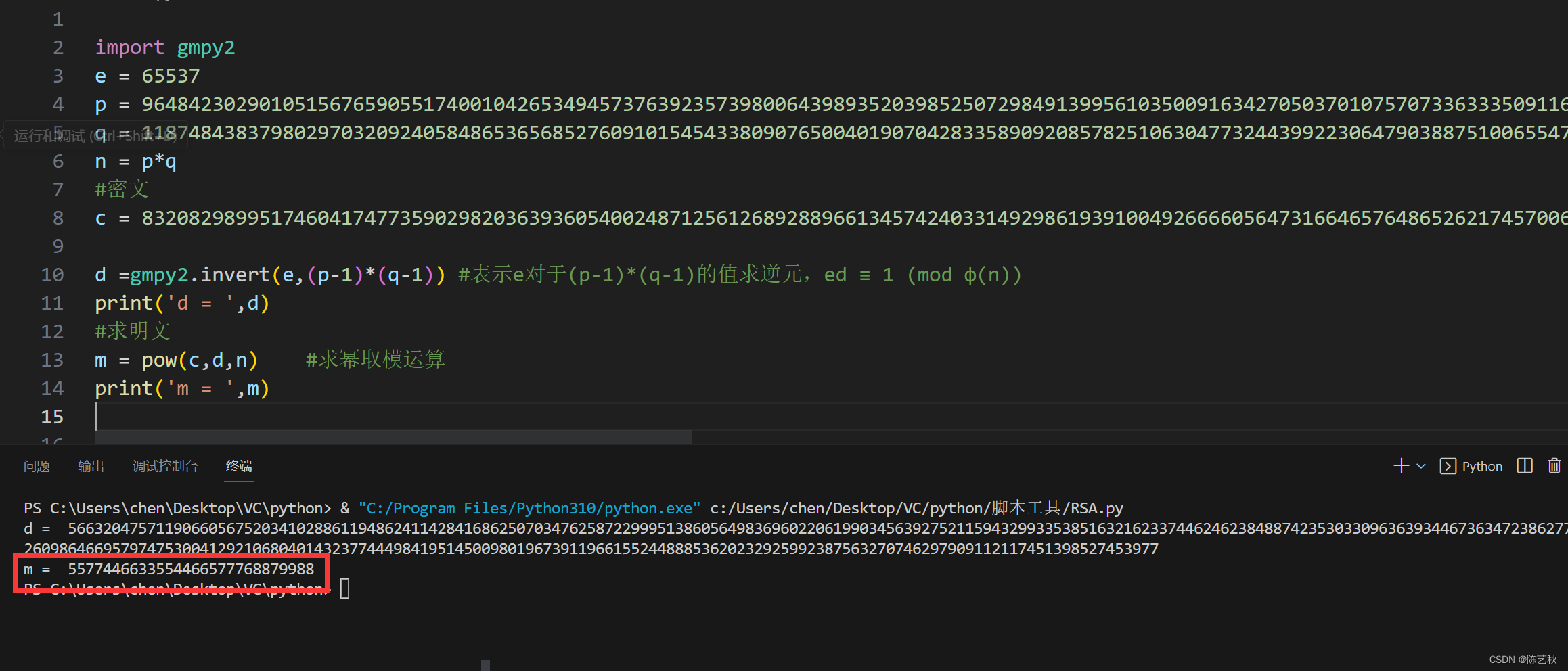
import gmpy2
e = 65537
p = 9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483
q = 11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407
n = p*q
#密文
c = 83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034
 
d =gmpy2.invert(e,(p-1)*(q-1)) #表示e对于(p-1)*(q-1)的值求逆元，ed ≡ 1 (mod φ(n))
print('d = ',d)
#求明文
m = pow(c,d,n)    #求幂取模运算
print('m = ',m)

最后解出的密文就是flag