第七章
- 最长重复子数组
- 题目理解
- 步骤
- dp含义
- 递推公式
- 初始化
- 为啥dp数组如此奇怪
- 遍历顺序
- 代码
- 最长公共子序列
- 题目理解
- 步骤
- dp含义
- 递推公式
- 初始化
- 遍历顺序
- 代码
- 总结
最长重复子数组
力扣链接
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
示例 1:
输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出:3
解释:长度最长的公共子数组是 [3,2,1] 。
示例 2:
输入:nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出:5
- 提示:
1 <= nums1.length, nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 100
题目理解
暴力解法就是 用两个for循环遍历两个数组, 然后在套用一个while循环或者for循环从各个起始位置开始判断
这样就相当于套用了三个for循环, 数据大了就会超时
其实本题采用的方法是动态规划, 用个二维dp数组来记录比较情况
步骤
dp含义
重复子数组, 里面有个暗含意思 连续
dp[i][j] — — 以下标 i - 1为结尾的nums1, 以下标 j - 1 结尾的nums2 之间的最长重复子数组的长度
🗨️为啥是以 下标 i - 1结尾 而不是以下标 i 结尾呢??
- 其实这也是为了
方便初始化 和 后续的判断
后面在为啥dp数组如此奇怪中有讲
递推公式
重复子数组, 里面有个暗含意思 连续
那么, 我们处理的方法 就和前面的 连续递增子序列 相同
if(nums1[i - 1] == nums2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
🗨️为啥比较的是 nums1[i - 1] 和 nums[j - 1], 而不是 nums1[i] 和 nums[j]呢
- dp数组的含义是 以下标 i - 1为结尾的nums1, 以下标 j - 1 结尾的nums 之间的最长重复子数组的长度
因为题目有连续的意思, 所以 dp[i][j] 的来源只有一个, 那就是 dp[i - 1][j - 1]
条件就是判断 当前两数组的值是否相等 — —nums1[i - 1] == nums2[ j - 1]
如果判断相等, 那么 dp[i][j] 就会在dp[i - 1][j - 1]的基础上 + 1 (两者都回退一步, 同时看看后面的值是否相等)
初始化
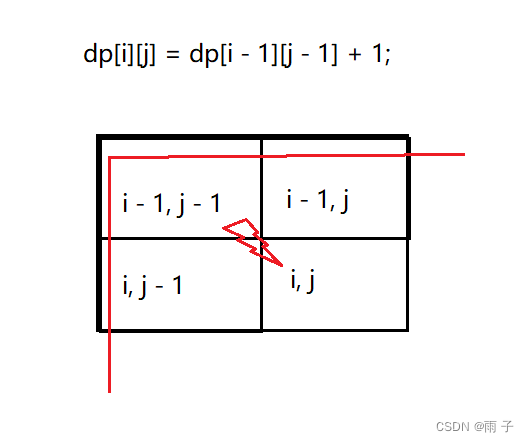
第一行 和 第一列要初始化一下.
那么我们需要初始化的是 dp[0][j] 和 dp[i][0]
但是, 我们定义的dp数组的含义 — — 以下标 i - 1为结尾的nums1, 以下标 j - 1 结尾的nums2 之间的最长重复子数组的长度
那么, 就是要初始化一下 -1行 和 -1列, 可想而知: 要初始化为 0
其它的要怎么初始化呢? — — 由前面到后面进行推导, 由上面到下面进行推导 — — 反正都是由前面的推导而来, 那么我们就初始化为 0
⇒
那么我们就全部都初始化为 0
vector<vector<int>> dp (nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
为啥dp数组如此奇怪
如果我们的dp数组的含义是 — — 以下标 i为结尾的nums1, 以下标 j为结尾的nums2之间的最长重复子数组的长度
那么, 初始化就要初始化 第1行 和 第 1列
如果nums1[i] 与 nums2[0] 相同的话,对应的 dp[i][0]就要初始为1, 因为此时最长重复子数组为1。 nums2[j] 与 nums1[0]相同的话,同理。
// 要对第一行,第一列经行初始化
for (int i = 0; i < nums1.size(); i++) if (nums1[i] == nums2[0]) dp[i][0] = 1;
for (int j = 0; j < nums2.size(); j++) if (nums1[0] == nums2[j]) dp[0][j] = 1;
遍历顺序
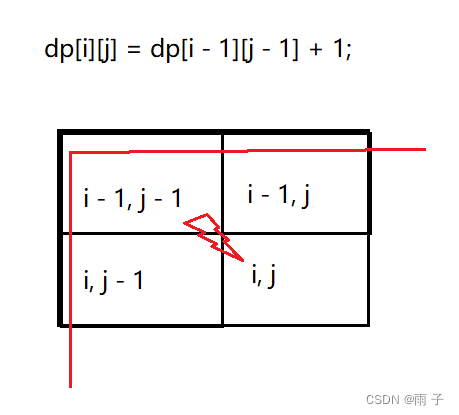
是从左上方开始递推的 — — 从前到后, 从上至下开始遍历
代码
class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2)
{
vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
int result = 0;
for(int i = 1; i <= nums1.size(); i++)
{
for(int j = 1; j <= nums2.size(); j++)
{
if(nums1[i - 1] == nums2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
result = max(result, dp[i][j]);
}
}
return result;
}
};
在这里, 我们也给出 dp数组的含义是 — — 下标以 i - 1为结尾的nums1, 下标以 j - 1为结尾的nums2之间的最长重复子序列的长度👇👇👇
class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2)
{
vector<vector<int>> dp(nums1.size(), vector<int>(nums2.size(), 0));
// 要对第一行,第一列经行初始化
for (int i = 0; i < nums1.size(); i++) if (nums1[i] == nums2[0]) dp[i][0] = 1;
for (int j = 0; j < nums2.size(); j++) if (nums1[0] == nums2[j]) dp[0][j] = 1;
int result = 0;
for(int i = 0; i < nums1.size(); i++)
{
for(int j = 0; j < nums2.size(); j++)
{
if(i > 0 && j > 0 && nums1[i] == nums2[j]) // 为了预防i - 1 和 j - 1是负数
dp[i][j] = dp[i - 1][j - 1] + 1;
result = max(result, dp[i][j]);
}
}
return result;
}
};

最长公共子序列
力扣链接
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 .
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串.
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列.
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列.
示例 1:
输入:text1 = “abcde”, text2 = “ace”
输出:3
解释:最长公共子序列是 “ace” ,它的长度为 3 。
示例 2:
输入:text1 = “abc”, text2 = “abc”
输出:3
解释:最长公共子序列是 “abc” ,它的长度为 3 。
示例 3:
输入:text1 = “abc”, text2 = “def”
输出:0
解释:两个字符串没有公共子序列,返回 0 。
- 提示:
1 <= text1.length, text2.length <= 1000
text1 和 text2 仅由小写英文字符组成
题目理解
这个题目是 不讲究连续 && 公共子序列
由此可以联想到 最长递增子序列
区别就是 : 一个是一个集合, 另一个是两个集合 — — 一个是一维dp数组, 另一个是二维dp数组
步骤
dp含义
dp[i][j] — — 区间为[0, i - 1]的nums1 和 区间为[0, j - 1]的nums2之间的最长公共子序列的长度
这里为啥是区间 i - 1 和 j - 1, 这个在上面已经说过了.
递推公式
无非就两种情况: nums1[i - 1] 和 nums2[j - 1] 是否相等
- 如果nums1[i - 1] == nums2[j - 1] — — 那么就使用dp[i - 1][j - 1]的情况 — — dp[i - 1][j - 1] + 1
- 如果nums1[i - 1] != nums2[j - 1] — — 那么就比较 区间为[0, i - 1]的nums1 和 区间为[0, j - 2]的nums2之间的最长公共子序列的长度(
dp[i][j - 1]) 和 区间为[0, i - 2]的nums1 和 区间为[0, j - 1]的nums2之间的最长公共子序列的长度(dp[i - 1][j])
⇒
if(nums1[i - 1] == nums2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
else
dp[i][j] = max(dp[i][j - 1], dp[i -1][j]);
初始化
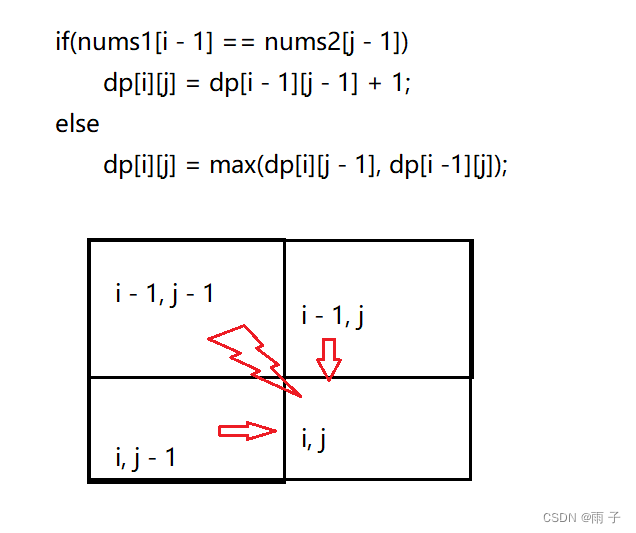
通过递推公式可知, 我们要初始化第一行 和 第一列
即我们需要初始化的是 dp[0][j] 和 dp[i][0]
但是, 我们dp数组的含义是 — — 区间为[0, i - 1]的nums1 和 区间为[0, j - 1]的nums2之间的最长公共子序列的长度
那么, dp[0][j] 的含义就是 -1 行 — — 那就初始化为 0 , dp[i][0]亦是如此
那么, 其他的dp数组呢? — — 由前面递推过来的, 所以就初始化为 0也是可以的
⇒
所以, 我们就把 dp数组都初始化为 0
遍历顺序
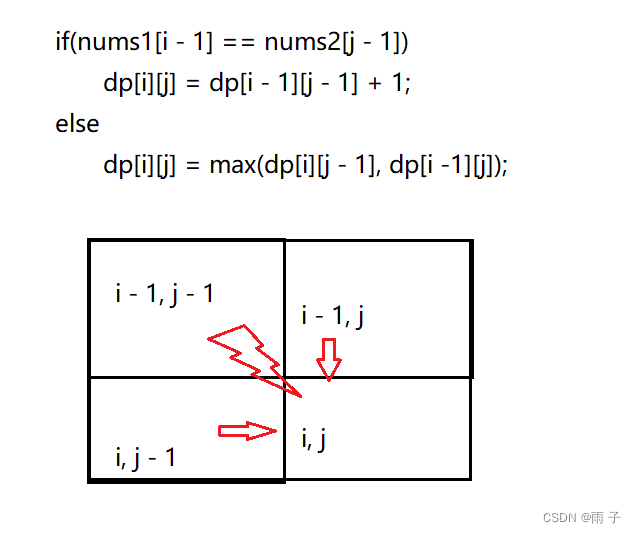
通过递推公式可知, 是 从前到后, 从上至下的顺序 --- --- 从小到大的遍历顺序
代码
class Solution {
public:
int longestCommonSubsequence(string text1, string text2)
{
vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));
for(int i = 1; i <= text1.size(); i++)
{
for(int j = 1; j <= text2.size(); j++)
{
if(text1[i - 1] == text2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
else
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
}
}
return dp[text1.size()][text2.size()];
}
};

总结
通过前面几章的动态规划刷题篇的训练, 我们不难发现
- dp数组的含义是非常重要的, 这也决定了后面的递推公式的得出
- 递推公式涉及 i - 1 或者是 j - 1的, 建议从 1开始遍历好一些, 这样也避免了一些情况的讨论
贵有恒,何必三更起五更眠;最无益,只怕一日曝十日寒 — — 毛泽东