文章目录

中级阶段
- 9.数据结构概述
- - 逻辑结构与存储结构
  - 时间复杂度、空间复杂度
- 10.11.12.线性表 (代码实战)
- - 线性表的定义、特点
  - 1.线性表的顺序存储(顺序表示)：顺序表
  - - 静态分配
    - 动态分配
    - 顺序表的定义、初始化、插入、删除、按值查找、按位查找操作 (代码)：
    - 命名规范（变量名、函数名）
  - 2.线性表的链式存储(链式表示)：链表（11、12）
  - - 头指针、头结点
    - 链表的定义
    - 链表的插入
    - - 头插法建立单链表
      - 尾插法建立单链表
      - 往第i个位置插入元素
    - 链表的查找
    - - 链表的按位置查找
      - 链表的按值查找
    - 链表的删除
    - 真题实战：2019年41题
    - 连续赋值
- 13.栈、队列
- - 1.栈
  - - 顺序栈
    - 链栈
  - 2.队列
  - - 循环队列
    - - 顺序存储(数组)：顺序队列 SqQueue
      - 链式队列(单链表) LinkQueue
      - 2019年42题：循环链式队列
- 14.树
- - 1.二叉树的存储
  - - 顺序存储：数组
    - 链式存储：二叉链表
  - 2.二叉树的建立（层次建树，辅助队列）
  - 3.二叉树的遍历
  - - 前序遍历
    - 中序遍历
    - 后序遍历
    - 层序遍历
  - 4.真题实战：2014年41题
  - 5.树OJ
- 15.查找
- - 1.顺序查找（线性查找）
  - - 哨兵
    - 线性查找代码
  - 2.折半查找（二分查找）
  - - 函数指针
    - 二分查找代码
  - 3.二叉排序树（二叉查找树） BST
  - - BST建树
- 16.17.18.排序
- - 1.冒泡排序
  - 2.快速排序
  - - 随机数生成
  - 3.直接插入排序
  - 16OJ
  - 4.(简单)选择排序
  - 5.堆排序
  - 6.归并排序
  - 所有排序算法的比较

中级阶段

9.数据结构概述

逻辑结构与存储结构

1.逻辑结构对人类友好，存储结构对计算机友好。中间有一道鸿沟，需要程序员来解决转换的问题。
2.数据的逻辑结构独立于存储结构

在这里插入图片描述

1.逻辑结构：集合结构、线性结构、树形结构、图形结构
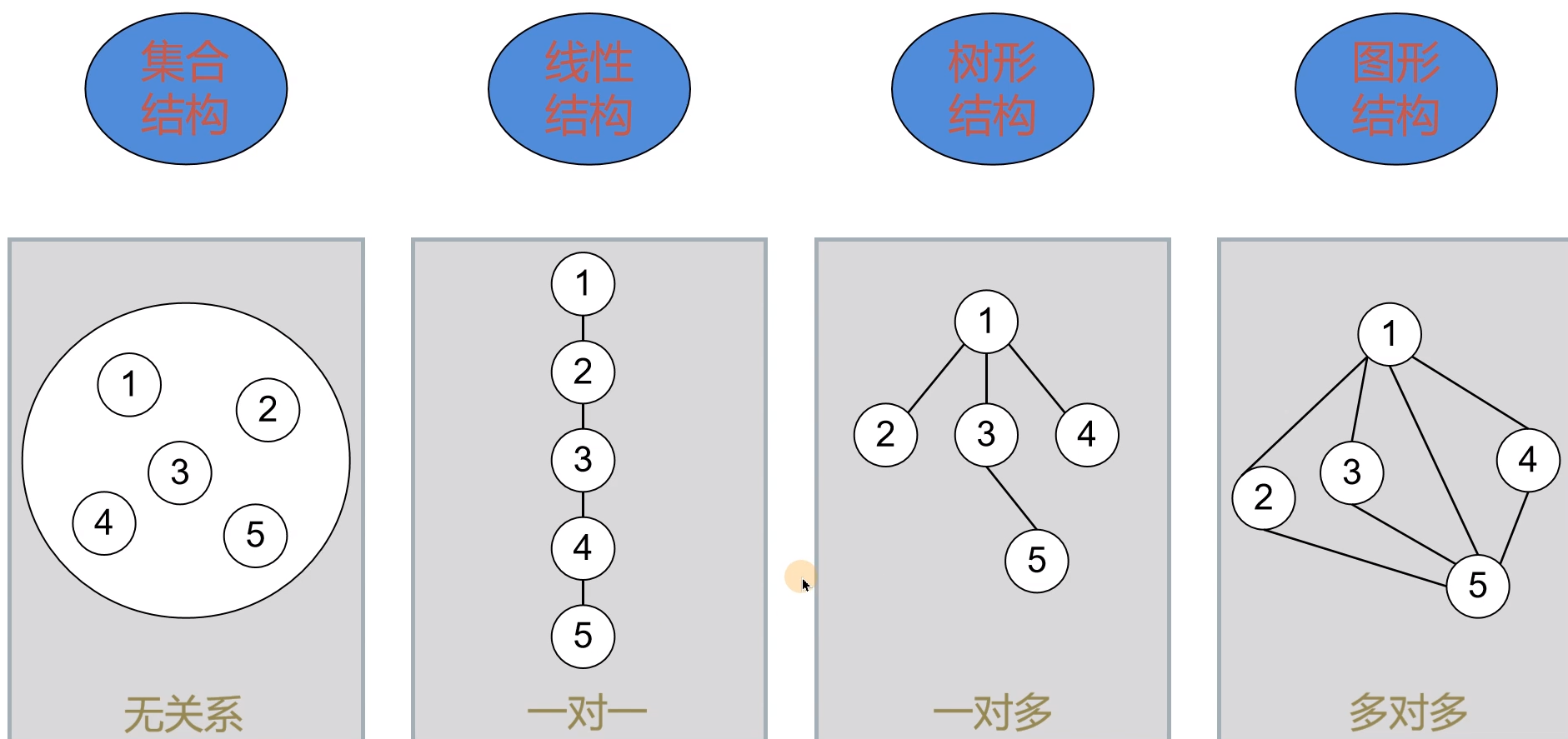
在这里插入图片描述

2.存储结构(物理结构)：顺序存储、链式存储、索引存储、散列存储
(1)顺序存储
优点：①随机访问、随机存取，方便查。 ②元素所占空间小，不需要像链式存储额外存一个指针
缺点：①增删不方便，需要移动。可能产生碎片。 ②需要整块连续的存储单元

随机访问、随机存取：可以直接一步到位的意思

(2)链式存储
优点：①增删方便，不需要移动元素，不会产生碎片 ②能充分利用所有存储单元，不需要整块的存储单元
缺点：①只能顺序存取，不方便查 ②所占空间大，每个元素需要额外存储一个指针

顺序存取：只能按照指针顺序一个接着一个地访问，从头到尾按个遍历，不能一步跳到目的地

在这里插入图片描述

时间复杂度、空间复杂度

1.算法
①算法的定义：对特定问题求解步骤的描述
②算法的特性：有穷性、确定性、可行性、输入、输出

2.时间复杂度
①时间复杂度的定义：算法中所有语句的频度(执行次数)之和，记为：T(N)=O(f(n))
②时间复杂度由低到高：O(1) < O(log₂n) < O(n) < O(nlog₂n) < O(n²) < O(n³) < O(2ⁿ) < O(n!)
在这里插入图片描述

在这里插入图片描述

10.11.12.线性表 (代码实战)

线性表的定义、特点

在这里插入图片描述

1.线性表的顺序存储(顺序表示)：顺序表

1.顺序表的定义：逻辑上相邻的元素，在物理位置上也相邻

静态分配

#define MaxSize 50 //顺序表最大长度
typedef struct{
	ElemType data[MaxSize];
	int len;  //顺序表实际长度
}SqList;

动态分配

#define InitSize 100
typedef struct{
    int *data;  //指示动态分配数组的指针
    int MaxSize,length;
}SeqList;

int main() {
    SeqList L;
    L.data = (int *)malloc(sizeof(int) * InitSize);
}

2.顺序表的优点、缺点

优点	缺点
①随机存取，查找效率高(根据首地址和元素序号)，时间复杂度O(1) ②存储密度高(每个结点只需要存储数据元素)	①(中间元素)插入、删除操作需要移动大量元素，效率低，时间复杂度O(n)【最后位置增删时间复杂度O(1)】 ②初始化时难以确定需要的存储空间的容量 ③存储分配必须要一整段连续的存储空间，不够灵活。

3.顺序表的插入
在这里插入图片描述

4.顺序表的删除操作
在这里插入图片描述

顺序表的定义、初始化、插入、删除、按值查找、按位查找操作 (代码)：

#include <cstdio>

//顺序表的定义
#define MaxSize 50
typedef int ElemType;  //为了后续顺序表改为存储其他数据类型，方便快速修改
typedef struct{
    ElemType data[MaxSize];
    int length;
}SqList;

//遍历打印顺序表的内容
void PrintList(SqList L){
    for(int i = 0; i < L.length; ++i){
        printf("%d ",L.data[i]);
    }
    printf("\n");
}

//顺序表的插入
bool ListInsert(SqList &L,int i,ElemType element){ //插入位置i(从1开始)。因为要改变L的内容，所以L要加引用
    if(i<1 || i > L.length+1) return false;//判断 位置i 是否合法
    if(L.length >= MaxSize) return false; //判断 顺序表 是否已满
    for(int j = L.length; j >= i; --j){   //插入位置之后的元素后移一位
        L.data[j] = L.data[j-1];
    }
    L.data[i-1] = element; //将元素插入第i个位置，下标为i-1
    L.length++;  //插入后，顺序表长度+1
    return true;
}

//顺序表的删除
bool ListDelete(SqList &L,int i,ElemType &del){ //要修改del，所以要加引用
    if(i<1 || i>L.length) return false; //先判断位置i是否合法
    del = L.data[i-1];  //保存删除值
    for(int j = i; j < L.length ; j++){ //元素往前一格
        L.data[j-1] = L.data[j];
    }
    L.length--;  //顺序表长度-1
    return true;
}

//顺序表的按值查找，返回位序
int LocateElem(SqList L,ElemType e){
    int i;
    for(i = 0; i < L.length; ++i){
        if(L.data[i] == e){
            return i+1;
        }
    }
    return 0;
}

//顺序表的按位置查找，返回对应位置的值
void GetElem(SqList L,int i){
    if(i>=1 && i<=L.length) printf("%d\n",L.data[i-1]);
    else                    printf("i位置非法");
}

int main() {
    //顺序表初始化
    SqList L;
    int ret; //ret用来装函数的返回值
    L.data[0] = 1;
    L.data[1] = 2;
    L.data[2] = 3;
    L.length = 3;
    printf("线性表初始化:");
    PrintList(L);
    printf("\n");

    //顺序表的插入
    ret = ListInsert(L,2,60);
    if(ret){
        printf("SqList insert successed\n");
        PrintList(L);
    }else{
        printf("SqList insert failed\n");
        PrintList(L);
    }
    printf("\n");

    //顺序表的删除
    ElemType del; //用del保存要删除的元素的值
    ret = ListDelete(L,1,del);
    if(ret){
        printf("SqList delete successed,del = %d\n",del);
        PrintList(L);
    }else{
        printf("SqList delete failed\n");
        PrintList(L);
    }
    printf("\n");

    //顺序表的按值查找
    int pos; //位序，第几个，从1开始
    pos = LocateElem(L,5);
    if(pos){
        printf("find this element,pos = %d\n",pos);
    }else{
        printf("don't find this element\n");
    }
    printf("\n");

    //顺序表的按位置查找
    int i;
    scanf("%d",&i);
    GetElem(L,i);
    return 0;
}

命名规范（变量名、函数名）

1.驼峰命名法：每个单词的首字母大写，ListInsert
2.下划线命名法：每个单词用下划线连接，list_insert

2.线性表的链式存储(链式表示)：链表（11、12）

任何数据结构，主要的操作就是增删查改

头指针、头结点

头指针指向头结点。
头结点作为单链表的第一个结点，一定存在，但考研中一般头结点数据域为空，仅为方便建立单链表而存在。有时候会存链表长度。
在这里插入图片描述

链表的定义

//单链表结点的定义
typedef int ElemType;
typedef struct LNode{
    ElemType data;      //数据域
    struct LNode *next; //指针域
}LNode,*LinkList;       //LinkList 和 LNode * 等价，都是结构体指针类型

LinkList 是一个指向单链表结构体的指针类型，而 next 是一个指向单链表结点结构体的指针类型。

单链表是由多个结点(Node)组成的结构，每个结点都包含两部分内容：数据域（Data）和指针域(Next)。其中，数据域存储结点的数据，指针域存储下一个结点的地址。
单链表结构体是由多个单链表结点组成的结构，它包含一个指向链表中第一个结点的指针(Head)和链表中结点的总数(Count)，这些信息为链表的操作提供了便利。
所以，单链表结点是单链表的基本组成单位，而单链表结构体则是对单链表进行整体的描述和管理。

链表的插入

单链表的遍历打印

//打印链表
void PrintList(LinkList L){
    L= L->next;
    while(L != NULL){
        printf("%d ",L->data);
        L = L->next;
    }
    printf("\n");
}

头插法建立单链表

//头插法新建链表
void ListHeadInsert(LinkList &L){
    L = (LNode *)malloc(sizeof(LNode));  //创建头结点 (LNode * 和 LinkList 完全等价)
    L->next = NULL;
    ElemType x;
    scanf("%d",&x);
    LinkList s; //第一个结点s， 等价于 LNode *s
    while(x != 9999){
        s = (LNode *)malloc(sizeof(LNode));
        s->data = x;
        s->next = L->next;
        L->next = s;
        scanf("%d",&x);
    }
}

尾插法建立单链表

需要引入一个尾指针r

//尾插法新建链表
void ListTailInsert(LinkList &L){
    L = (LNode *)malloc(sizeof(LNode));
    L->next = NULL;
    ElemType x;
    scanf("%d",&x);
    LNode *s, *r = L;
    while(x != 9999){
        s = (LNode *)malloc(sizeof(LNode));
        s->data = x;
        r->next = s;
        r = s;
        scanf("%d",&x);
    }
    r->next = NULL;
}

工作的最高境界，代码即注释

例题：王道OJ11
提交网址：http://oj.lgwenda.com/problem/17
在这里插入图片描述

#include <cstdio>
#include <cstdlib>

typedef struct LNode{
    int data;
    struct LNode *next;
}LNode,*LinkList;

//打印链表中每个结点的值
void PrintList(LinkList L){
    L=L->next;
    while(L!=NULL){
        printf("%d",L->data);//打印当前结点数据
        L=L->next;//指向下一个结点
        if(L!=NULL){
            printf(" ");
        }
    }
    printf("\n");
}

//头插法创建单链表
void ListHeadInsert(LinkList &L){
    LinkList s;
    int x;
    scanf("%d",&x);
    while(x != 9999){
        s = (LinkList)malloc(sizeof(LNode));
        s->data = x;
        s->next = L->next;
        L->next = s;
        scanf("%d",&x);
    }
}

//尾插法创建单链表
void ListTailInsert(LinkList &L){
    int x;
    scanf("%d",&x);
    LinkList s,r=L; //尾指针r
    while(x != 9999){
        s = (LinkList)malloc(sizeof(LNode));
        s->data = x;
        r->next = s;
        r = s;
        scanf("%d",&x);
    }
    r->next = NULL;
}

int main(){
    //创建单链表
    LinkList L; //定义链表的头指针
    L = (LinkList)malloc(sizeof(LNode));
    L->next = NULL;

    ListHeadInsert(L);
    PrintList(L);

    ListTailInsert(L);
    PrintList(L);
    return 0;
}

往第i个位置插入元素

//在第i个位置插入元素elem
void ListMiddleInsert(LinkList L,int i,ElemType elem){
	if(i<1){
		printf("位置i应为正整数\n");
		return;
	}
    for(int j = 0; j<i-1 && L!=NULL; ++j){
        L =L->next;
    }
    if(L != NULL){
        LinkList s = (LNode *)malloc(sizeof(LNode));
        s->data = elem;
        s->next = L->next;
        L->next = s;
    }else{ //L == NULL
        printf("位置i不合法\n");
    }
}

链表的查找

链表的按位置查找

//单链表按位置查询，查询第i个位置元素的值
void GetElem(LinkList L,int i){
    for(int j = 0; j<i && L!=NULL; ++j){
        L = L->next;
    }
    if(L == NULL){
        printf("位置i超出链表长度\n");
    }else{
        printf("位置i=%d的元素为%d\n",i,L->data);
    }
}

在这里插入图片描述

链表的按值查找

//单链表按值查询，查询值为elem的元素是否在单链表中存在
void LocateElem(LinkList L,ElemType elem){
    while(L != NULL){
        if(elem == L->data){
            printf("存在元素elem=%d\n",elem);
            return;
        }else{
            L = L->next;
        }
    }
    printf("the elem=%d is not exist\n",elem);
}

链表的删除

//单链表的删除：删除第i个位置的结点
void ListDelete(LinkList L,int i,ElemType &e){  //删除时，L不会变化，不需要加引用
    if(i<1){ //判断i是否合法
        printf("位置i应为正整数\n");
        return;
    }
    LinkList p = L;
    for(int j = 0; j<i-1 && p!=NULL; ++j){  //使p指向第i-1个位置
        p = p->next;
    }
    if(p && p->next){ //此时p指向i-1位置，p->next指向第i个位置。或 p已为NULL,则p->next会报错
        LinkList q = p->next;
        e = q->data;
        p->next = q->next; //断链
        free(q);
    }else{
        printf("位置i超出链表长度\n");
    }
}

在这里插入图片描述

真题实战：2019年41题

#include <cstdio>
#include <cstdlib>

typedef struct node{
    int data;
    struct node *next;
}Node;

//打印链表(带头结点)
void PrintList(Node* L){
    L= L->next;
    while(L != NULL){
        printf("%d ",L->data);
        L = L->next;
    }
    printf("\n");
}

//打印链表(不带头结点)
void PrintList2(Node* L){
    while(L != NULL){
        printf("%d ",L->data);
        L = L->next;
    }
    printf("\n");
}

//尾插法建立单链表
void ListTailInsert(Node * &L){
    L = (Node *)malloc(sizeof(Node));
    L->next = NULL;
    int x;
    scanf("%d",&x);
    Node *s, *r = L;
    while(x != 9999){
        s = (Node *)malloc(sizeof(Node));
        s->data = x;
        r->next = s;
        r = s;
        scanf("%d",&x);
    }
    r->next = NULL;
}

//寻找中间结点的指针
Node * FindMiddle(Node * L){
    Node *p1=L,*p2=L;
    while(p2 != NULL){ //p2走两步，p1走一步。直至p2为NULL
        p2=p2->next;
        if(p2) p2 = p2->next;
        else   break;
        p1 = p1->next;
    }
    return p1;
}

//链表原地逆置
void ListReverse(Node * &L2){
    Node *r=L2,*s,*t;
    if(r==NULL)  return; //L2只有0个结点
    if(r->next != NULL){
        s = r->next;
    }else{  //L2只有1个结点
        return;
    }
    if(s->next != NULL){
        t = s->next;
    }else{  //L2只有2个结点
        s->next = r;
        L2 = s;
        r->next = NULL;
        return;
    }

    while(t){
        s->next = r;
        r = s;
        s = t;
        t = t->next;
    }
    s->next = r;
    L2->next = NULL;
    L2 = s;
}

//交替合并
void ListMerge(Node *&L,Node *L2){
    Node *pcur=L->next,*p1=pcur,*p2=L2;
    while(p2!=NULL){
        p1 = p1->next;

        pcur->next = p2;
        pcur = p2;
        p2 = p2->next;

        pcur->next = p1;
        pcur = p1;
    }
    pcur->next = NULL;
}

int main() {
    Node * L,*L2; //L带头结点，L2不带头结点
    ListTailInsert(L);
    PrintList(L);

    L2 = FindMiddle(L);
    printf("%d\n",L2->data);

    L2 = L2->next; //中间结点是第一段链表的尾结点，下一个是第二段链表的头结点
    ListReverse(L2); //后半段链表原地逆置
    PrintList2(L2);

    ListMerge(L,L2);
    PrintList(L);
    return 0;
}

连续赋值

C语言可以连续赋值，但是必须先声明

int a=1,b=1,c=1; //边定义边初始化

等价于

int a,b,c; 
a=b=c=1; //连续赋值

13.栈、队列

1.栈

顺序栈

1.定义

#define MaxSize 50    //定义栈中元素最大个数
typedef struct{
    int data[MaxSize];//静态数组存放栈中元素
    int top;          //栈顶指针
}SqStack;

2.初始化

void InitStack(SqStack &S){
    S.top = -1;
}

3.入栈 Push

bool Push(SqStack &S,int x){
    if(S.top == MaxSize-1) return false;  //判栈满
	S.data[++S.top];
	return true;
}

4.出栈 / 弹栈 Pop

bool Pop(SqStack &S,int &x){
    if(S.top == -1) return false; //判断栈空
    x = S.data[S.top--];
    return true;
}

5.判栈空

bool StackEmpty(SqStack S){
    if(S.top == -1){
        return true;
    }
    return false;
}

6.获取栈顶元素

//获取栈顶元素
void GetTop(SqStack S,int &x){
    if(S.top == -1){
        printf("stack is empty,GetTop failed.\n");
        return;
    }
    x = S.data[S.top];
}

7.遍历栈

//遍历栈
void PrintStack(SqStack S){
    if(S.top == -1){
        printf("stack is empty\n");
        return;
    }
    while(S.top != -1){
        printf("%d ",S.data[S.top]);
        S.top--;
    }
    printf("\n");
}

链栈

1.链栈的定义、初始化

typedef struct LinkNode{
	int data;              //数据域
	struct LinkNode *next; //指针域
}LinkNode,*LiStack;   //栈类型定义

2.进栈
在头结点后插入，头插法

3.出栈
在头结点后删除

x = top->data;
L->next = top->next;
free(top);
top = L->next;

4.栈空：L->next = NULL

5.栈满
只要还存在剩余内存，链栈就不会满。可以继续申请空间，添加元素。

2.队列

队列(Queue)，简称队，也是一种操作受限的线性表，只允许在表的一端进行插入，而在表的另一端进行删除。允许删除的一端叫队尾，允许插入的一端叫队头/队首。队头出队，队尾入队。特点是先进先出，FIFO。
在这里插入图片描述

循环队列

顺序存储(数组)：顺序队列 SqQueue

1.顺序队列的定义：

#define MaxSize 50
typedef struct{
    int data[MaxSize]; //最多存储MaxSize-1个元素
    int front,rear;
}SqQueue;

2.判断队空：Q.rear == Q.front
3.判断队满：(Q.rear+1)%MaxSize == Q.front
4.初始化

void InitQueue(SqQueue &Q){
    Q.front = Q.rear = 0;
}

5.入队

bool EnQueue(SqQueue &Q,int x){
    if((Q.rear+1)%MaxSize == Q.front)  return false; //判断队满
    Q.data[Q.rear] = x;
    Q.rear = (Q.rear+1)%MaxSize;  //循环队列
    return true;
}

6.出队

bool DeQueue(SqQueue &Q,int &x){
    if(Q.rear == Q.front){//判断队空
    	return false; 
    } 
    x = Q.data[Q.front];   //队头出队
    Q.front = (Q.front+1)%MaxSize;  //循环队列
    return true;
}

7.打印队列

void PrintQueue(SqQueue Q){
    while(Q.front != Q.rear){
        printf("%d ",Q.data[Q.front++]);
    }
    printf("\n");
}

8.示意图
在这里插入图片描述

链式队列(单链表) LinkQueue

带头结点的链式队列，front指向头结点，front->next指向队头元素，rear指向队尾元素

1.定义

typedef struct LinkNode{
	int data;
	struct LinkNode *next;
}LinkNode;

typedef struct{
	LinkNode *front,*rear;
}LinkQueue;

2.初始化

void InitQueue(LinkQueue &Q){
    Q.front=Q.rear=(LinkNode *)malloc(sizeof(LinkNode));
    Q.front->next = NULL;
}

3.入队

void EnQueue(LinkQueue &Q,int x){
    LinkNode *p = (LinkNode *)malloc(sizeof(LinkNode));
    p->data = x;
    p->next = NULL;
    Q.rear->next = p;
    Q.rear = p;
}

4.出队

bool DeQueue(LinkQueue &Q,int &x){
    if(Q.rear == Q.front) return false; //判队空
    LinkNode *q = Q.front->next;
    x = q->data;
    Q.front->next = q->next;
  //if(Q.front->next == NULL) Q.rear = NULL;//若删除的是最后一个元素
    if(Q.rear == q) Q.rear = Q.front; //若删除的是最后一个元素
    free(q);
    return true;
}

5.判队空

//判断队列是否为空
bool IsEmpty(LinkQueue Q){
    return Q.rear == Q.front;
}

6.打印队列

//打印队列
void PrintQueue(LinkQueue Q){
    LinkNode *p = Q.front->next;
    while(p){
        printf("%d ",p->data);
        p = p->next;
    }
    printf("\n");
}

2019年42题：循环链式队列

在这里插入图片描述

答案：
(1)链式存储结构
(2)链式循环队列
判队空：Q.rear == Q.front
判队满：Q.rear->next == Q.front

队列初始状态：
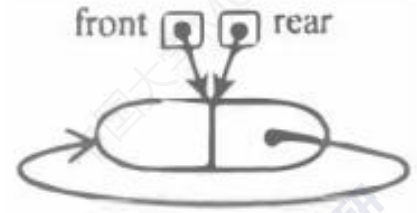
在这里插入图片描述

(3)插入一个元素后的状态
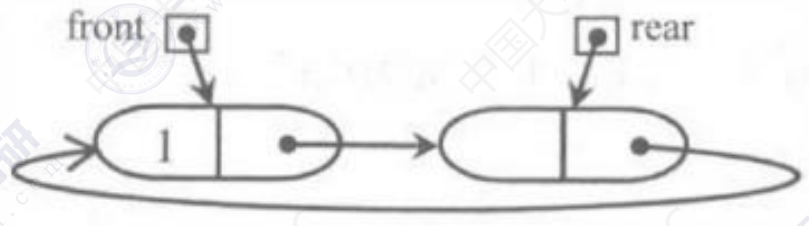
在这里插入图片描述

(4)入队出队基本操作
①入队：队尾入队，判队满

void EnQueue(LinkQueue &Q,int x){
	if(Q.rear->next == Q.front){ //判队满
		LinkNode *p = (LinkNode *)malloc(sizeof(LinkNode));
		p = Q.rear->next;
		p->next = Q.front;
	}
	Q.rear->data = x;
	Q.rear = Q.rear->next;
}

②出队：队头出队，判队空

bool DeQueue(LinkQueue &Q,int &x){
	if(Q.rear == Q.front){ //判队空
		return false;
	}
	x = Q.front->data;
	Q.front = Q.front->next;
	return true;
}

14.树

1.二叉树的存储

顺序存储：数组

在这里插入图片描述

链式存储：二叉链表

typedef struct BiTNode{
	char data;
	struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

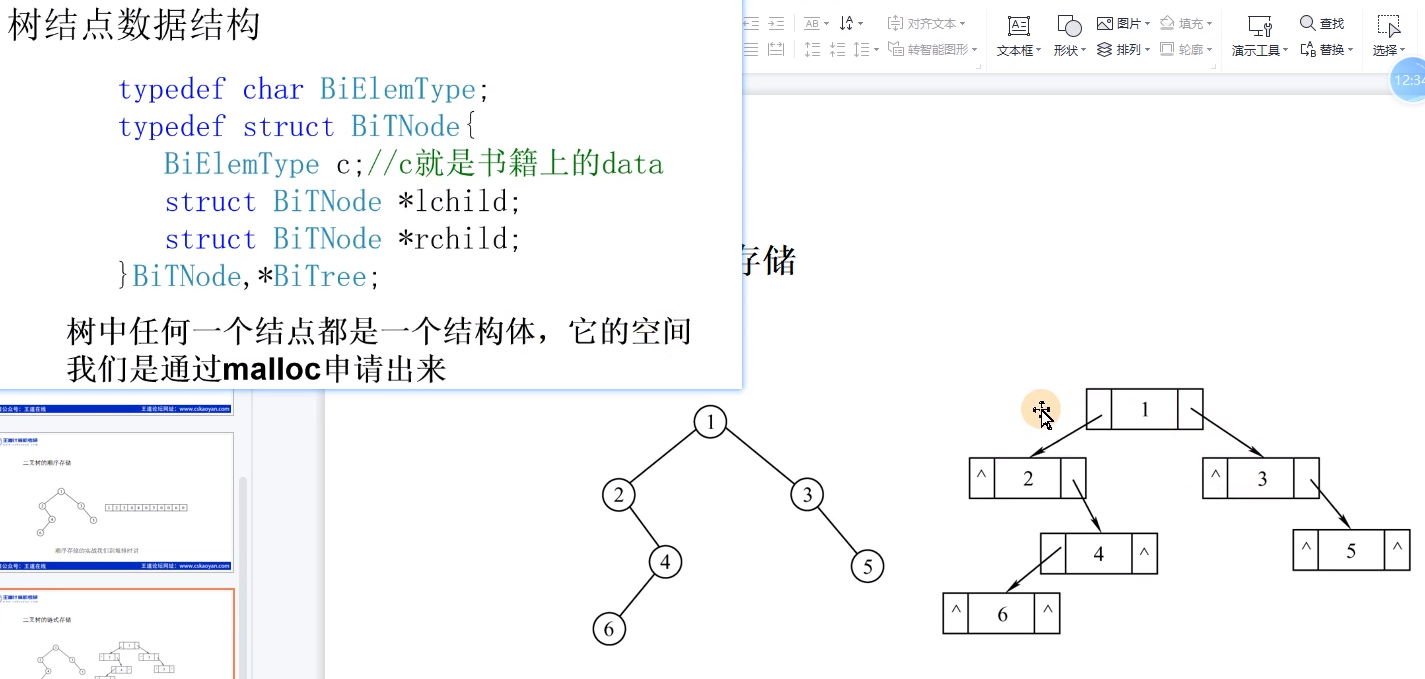
在这里插入图片描述

2.二叉树的建立（层次建树，辅助队列）

function.h

#ifndef TREE_FUNCTION_H
#define TREE_FUNCTION_H

#include <cstdio>
#include <cstdlib>

typedef struct BiTNode{
    char data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

//tag结构体:辅助队列,层次建树使用的
typedef struct tag{
    BiTree p;          //树某一结点的地址值
    struct tag *pnext;
}tag,*ptag;

#endif //TREE_FUNCTION_H

main.cpp

#include "function.h"

//二叉树层次建树
int main() {
    BiTree pnew; //用来指向新申请的树结点
    BiTree tree = NULL; //指向树的根结点，代表树
    //phead队列头，ptail队列尾
    //listpnew指向新入队元素,pcur队列中当前树中的父亲结点
    ptag phead = NULL, ptail = NULL,listpnew = NULL,pcur = NULL;

    char c;
    while(scanf("%c",&c)){
        if(c == '\n') break;
        pnew = (BiTree)calloc(1,sizeof(BiTNode)); //calloc申请空间，并初始化为0
        pnew->data = c;
        listpnew = (ptag)calloc(1,sizeof(tag)); //给队列结点申请空间，并初始化为0
        listpnew->p = pnew;

        if(tree == NULL){ //若树为空
            tree = pnew;
            phead = ptail = pcur =listpnew;
        }else{
            //元素先入队列
            ptail->pnext = listpnew; //元素入队
            ptail = listpnew;  //队尾指针后移
            //再加入树中
            if(pcur->p->lchild == NULL){ //左子树为空，放入左孩子
                pcur->p->lchild = pnew;
            }else if(pcur->p->rchild == NULL){ //右子树为空，放入右孩子
                pcur->p->rchild = pnew;
                pcur = pcur->pnext;//放入右孩子后，当前父结点已满，pcur需要指向队列下一个父亲
            }else{ //左右子树均不为空，
                printf("wrong\n");
            }
        }
    }
    return 0;
}

在这里插入图片描述

3.二叉树的遍历

前序遍历

前序遍历：根左右。[先序遍历，树的深度优先遍历]

void PreOrder(BiTree p){
    if(p != NULL){ //根不为空,左孩子不为空,右孩子不为空
        printf("%c",p->data);
        PreOrder(p->lchild);
        PreOrder(p->rchild);
    }
}

中序遍历

中序遍历：左根右。相当于把一棵树从上往下踩扁，变成一条线，得到的序列。

void InOrder(BiTree p){
    if(p != NULL){
        InOrder(p->lchild);
        printf("%c",p->data);
        InOrder(p->rchild);
    }
}

后序遍历

//后序遍历:左右根
void PostOrder(BiTree p){
    if(p != NULL){
        PostOrder(p->lchild);
        PostOrder(p->rchild);
        printf("%c",p->data);
    }
}

层序遍历

层序遍历：层次遍历，树的广度优先遍历

void LevelOrder(BiTree T){
    LinkQueue Q;
    InitQueue(Q);
    BiTree p;     //存储出队结点
    EnQueue(Q,T); //根结点入队
    while(!IsEmpty(Q)){
        DeQueue(Q,p);  //队头结点出队
        putchar(p->data); //putchar输出单个字符,等价于 printf("%c",p->data);
        if(p->lchild != NULL){
            EnQueue(Q,p->lchild); //左孩子不为空,左孩子入队
        }
        if(p->rchild != NULL){
            EnQueue(Q,p->rchild); //右孩子不为空，右孩子入队
        }
    }
}

层次遍历完整运行代码：
function.h

#ifndef TREE_FUNCTION_H
#define TREE_FUNCTION_H

#include <cstdio>
#include <cstdlib>

typedef struct BiTNode{
    char data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

//tag结构体:辅助队列,层次建树使用的
typedef struct tag{
    BiTree p;          //树某一结点的地址值
    struct tag *pnext;
}tag,*ptag;


//链队列
typedef struct LinkNode{
    BiTree data;
    struct LinkNode *next;
}LinkNode;

typedef struct{
    LinkNode *front,*rear;
}LinkQueue;

void InitQueue(LinkQueue &Q);//初始化
void EnQueue(LinkQueue &Q,BiTree x);//入队
bool DeQueue(LinkQueue &Q,BiTree &x);//出队
bool IsEmpty(LinkQueue Q);
void PrintQueue(LinkQueue Q);//打印队列

#endif //TREE_FUNCTION_H

queue.cpp

#include "function.h"

//初始化
void InitQueue(LinkQueue &Q){
    Q.front=Q.rear=(LinkNode *)malloc(sizeof(LinkNode));
    Q.front->next = NULL;
}

//入队
void EnQueue(LinkQueue &Q,BiTree x){
    LinkNode *p = (LinkNode *)malloc(sizeof(LinkNode));
    p->data = x;
    p->next = NULL;
    Q.rear->next = p;
    Q.rear = p;
}

//出队(带头结点)
bool DeQueue(LinkQueue &Q,BiTree &x){
    if(Q.rear == Q.front) return false; //判队空
    LinkNode *q = Q.front->next;  //带头结点，删除头结点后面的一个结点  
    x = q->data;   //用x返回队头元素,x加了引用
    Q.front->next = q->next;  //修改头结点的next指针,逻辑上删除q所指结点
    //if(Q.front->next == NULL) Q.rear = NULL;//若删除的是最后一个元素
    if(Q.rear == q) Q.rear = Q.front; //若删除的是最后一个元素
    free(q);
    return true;
}

//判断队列是否为空
bool IsEmpty(LinkQueue Q){
    return Q.rear == Q.front;
}

//打印队列
void PrintQueue(LinkQueue Q){
    LinkNode *p = Q.front->next;
    while(p){
        printf("%d ",p->data);
        p = p->next;
    }
    printf("\n");
}

main.cpp

#include "function.h"

//前序遍历:根左右
void PreOrder(BiTree p){
    if(p != NULL){ //根不为空,左孩子不为空,右孩子不为空
        printf("%c",p->data);
        PreOrder(p->lchild);
        PreOrder(p->rchild);
    }
}

//中序遍历:左根右
void InOrder(BiTree p){
    if(p != NULL){
        InOrder(p->lchild);
        printf("%c",p->data);
        InOrder(p->rchild);
    }
}

//后序遍历:左右根
void PostOrder(BiTree p){
    if(p != NULL){
        PostOrder(p->lchild);
        PostOrder(p->rchild);
        printf("%c",p->data);
    }
}

//层序遍历
void LevelOrder(BiTree T){
    LinkQueue Q;
    InitQueue(Q);
    BiTree p;     //存储出队结点
    EnQueue(Q,T); //根结点入队
    while(!IsEmpty(Q)){
        DeQueue(Q,p);  //队头结点出队
        putchar(p->data); //putchar输出单个字符,等价于 printf("%c",p->data);
        if(p->lchild != NULL){
            EnQueue(Q,p->lchild); //左孩子不为空,左孩子入队
        }
        if(p->rchild != NULL){
            EnQueue(Q,p->rchild); //右孩子不为空，右孩子入队
        }
    }
}

//二叉树层次建树
int main() {
    BiTree pnew; //用来指向新申请的树结点
    BiTree tree = NULL; //指向树的根结点，代表树
    //phead队列头，ptail队列尾
    //listpnew指向新入队元素,pcur队列中当前树中的父亲结点
    ptag phead = NULL, ptail = NULL,listpnew = NULL,pcur = NULL;

    char c;
    while(scanf("%c",&c)){ //abcdefghij
        if(c == '\n') break;
        pnew = (BiTree)calloc(1,sizeof(BiTNode)); //calloc申请空间，并初始化为0
        pnew->data = c;
        listpnew = (ptag)calloc(1,sizeof(tag)); //给队列结点申请空间，并初始化为0
        listpnew->p = pnew;

        if(tree == NULL){ //若树为空
            tree = pnew;
            phead = ptail = pcur =listpnew;
        }else{
            //元素先入队列
            ptail->pnext = listpnew; //元素入队
            ptail = listpnew;  //队尾指针后移
            //再加入树中
            if(pcur->p->lchild == NULL){ //左子树为空，放入左孩子
                pcur->p->lchild = pnew;
            }else if(pcur->p->rchild == NULL){ //右子树为空，放入右孩子
                pcur->p->rchild = pnew;
                pcur = pcur->pnext;//放入右孩子后，当前父结点已满，pcur需要指向队列下一个父亲
            }else{ //左右子树均不为空，
                printf("wrong\n");
            }
        }
    }

    PreOrder(tree);
    printf("\n");

    InOrder(tree);
    printf("\n");

    PostOrder(tree);
    printf("\n");

    LevelOrder(tree);
    printf("\n");

    return 0;
}

4.真题实战：2014年41题

带权路径长度WPL：Weighted Path Length of Tree
树的带权路径长度：每个叶结点的深度与权值之积的总和。

核心代码：

int WPL = 0; //全局变量WPL

void PreOrder(BiTree p,int deep){
    if(p != NULL){ //根不为空,左孩子不为空,右孩子不为空
        //printf("%d----%d\n",p->weight,deep);
        if(p->left==NULL && p->right==NULL){ //左右子树均为空,为叶子结点
            WPL += deep * p->weight;
        }
        PreOrder(p->left,deep+1);
        PreOrder(p->right,deep+1);
    }
}

int main(){
	PreOrder(root,0);
	printf("%d\n",WPL);
	return 0;
}

完整运行代码：

#include <cstdio>
#include <cstdlib>

int WPL = 0; //全局变量WPL

typedef struct BiTNode{
    int weight;
    struct BiTNode *left,*right;
}BiTNode,*BiTree;

//tag结构体:辅助队列,层次建树使用的
typedef struct tag{
    BiTree p;          //树某一结点的地址值
    struct tag *pnext;
}tag,*ptag;

void PreOrder(BiTree p,int deep){
    if(p != NULL){ //根不为空,左孩子不为空,右孩子不为空
        //printf("%d----%d\n",p->weight,deep);
        if(p->left==NULL && p->right==NULL){ //左右子树均为空,为叶子结点
            WPL += deep * p->weight;
        }
        PreOrder(p->left,deep+1);
        PreOrder(p->right,deep+1);
    }
}

int main() {
    BiTree pnew; //用来指向新申请的树结点
    BiTree root = NULL; //指向树的根结点，代表树
    //phead队列头，ptail队列尾
    //listpnew指向新入队元素,pcur队列中当前树中的父亲结点
    ptag phead = NULL, ptail = NULL,listpnew = NULL,pcur = NULL;

    int c;
    while(scanf("%d",&c)){ //1 2 3 4 5 6 7 0
        if(c == 0) break;
        pnew = (BiTree)calloc(1,sizeof(BiTNode)); //calloc申请空间，并初始化为0
        pnew->weight = c;
        listpnew = (ptag)calloc(1,sizeof(tag)); //给队列结点申请空间，并初始化为0
        listpnew->p = pnew;

        if(root == NULL){ //若树为空
            root = pnew;
			phead = ptail = pcur =listpnew;
        }else{
            //元素先入队列
            ptail->pnext = listpnew; //元素入队
            ptail = listpnew;  //队尾指针后移
            //再加入树中
            if(pcur->p->left == NULL){ //左子树为空，放入左孩子
                pcur->p->left = pnew;
            }else if(pcur->p->right == NULL){ //右子树为空，放入右孩子
                pcur->p->right = pnew;
                pcur = pcur->pnext;//放入右孩子后，当前父结点已满，pcur需要指向队列下一个父亲
            }else{ //左右子树均不为空，
                printf("wrong\n");
            }
        }
    }

    PreOrder(root,0);
    printf("%d\n",WPL);
    return 0;
}

5.树OJ

1.OJ1
要求：层次建树，前序遍历
提交网站：http://oj.lgwenda.com/problem/20
在这里插入图片描述

完整代码：

#include <cstdio>
#include <cstdlib>

typedef struct BiTNode{
    char data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

typedef struct tag{
    BiTree p;   树某一结点的地址值
    struct tag *next;
}tag_t,*ptag_t;

//前序遍历，根左右
void PreOrder(BiTree T){
    if(T != NULL){
        printf("%c",T->data);
        PreOrder(T->lchild);
        PreOrder(T->rchild);
    }
}

int main() {
    BiTree pnew; //pnew指向新申请的树结点
    BiTree root = NULL; //root指向树的根结点，代表树
    ptag_t phead = NULL,ptail = NULL,pcur = NULL,listpnew = NULL; //队列头尾指针,pcur当前父结点,listpnew新入队元素

    char c;
    while(scanf("%c",&c)){
        if(c == '\n') break;
        pnew = (BiTree)calloc(1,sizeof(BiTNode)); //calloc申请空间，并初始化为0
        pnew->data = c;
        listpnew = (ptag_t)calloc(1,sizeof(tag_t)); //给队列结点申请空间，并初始化为0
        listpnew->p = pnew;

        if(root == NULL){  //若树为空
            root = pnew;
            phead = ptail = pcur = listpnew;
        }else{ //树非空
            //元素先入队列
            ptail->next = listpnew;  //元素入队
            ptail = listpnew;        //队尾指针后移
            //再加入树中
            if(pcur->p->lchild == NULL){ //若左子树为空，加入左子树
                pcur->p->lchild = pnew;
            }else if(pcur->p->rchild == NULL){ //若右子树为空，加入右子树
                pcur->p->rchild = pnew;
                pcur = pcur->next;
            }
        }
    }
    PreOrder(root);
    return 0;
}

2.OJ2
要求：层次建树，中序后序层序遍历
提交网址：http://oj.lgwenda.com/problem/21
在这里插入图片描述

完整代码：

#include <cstdio>
#include <cstdlib>

//树结点
typedef struct BiTNode{
    char data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
//层次建树辅助队列
typedef struct tag{
    BiTree p;   树某一结点的地址值
    struct tag *next;
}tag_t,*ptag_t;

//链队列结点
typedef struct LinkNode{
    BiTree data;
    struct LinkNode *next;
}LinkNode;
//链队列
typedef struct{
    LinkNode *front,*rear;
}LinkQueue;

//初始化
void InitQueue(LinkQueue &Q){
    Q.front=Q.rear=(LinkNode *)malloc(sizeof(LinkNode));
    Q.front->next = NULL;
}
//入队
void EnQueue(LinkQueue &Q,BiTree x){
    LinkNode *p = (LinkNode *)malloc(sizeof(LinkNode));
    p->data = x;
    p->next = NULL;
    Q.rear->next = p;
    Q.rear = p;
}
//出队
bool DeQueue(LinkQueue &Q,BiTree &x){
    if(Q.rear == Q.front) return false; //判队空
    LinkNode *q = Q.front->next;
    x = q->data;
    Q.front->next = q->next;
    //if(Q.front->next == NULL) Q.rear = NULL;//若删除的是最后一个元素
    if(Q.rear == q) Q.rear = Q.front; //若删除的是最后一个元素
    free(q);
    return true;
}
//判断队列是否为空
bool IsEmpty(LinkQueue Q){
    return Q.rear == Q.front;
}

//前序遍历，根左右
void PreOrder(BiTree T){
    if(T != NULL){
        printf("%c",T->data);
        PreOrder(T->lchild);
        PreOrder(T->rchild);
    }
}
//中序遍历，左根右
void InOrder(BiTree T){
    if(T != NULL){
        InOrder(T->lchild);
        printf("%c",T->data);
        InOrder(T->rchild);
    }
}
//后序遍历，左右根
void PostOrder(BiTree T){
    if(T != NULL){
        PostOrder(T->lchild);
        PostOrder(T->rchild);
        printf("%c",T->data);
    }
}
//层序遍历
void LevelOrder(BiTree T){
    LinkQueue Q;
    InitQueue(Q);
    BiTree p;
    EnQueue(Q,T); //树的根结点入队
    while(!IsEmpty(Q)){
        DeQueue(Q,p); //队头结点出队
        putchar(p->data);
        if(p->lchild != NULL){
            EnQueue(Q,p->lchild);
        }
        if(p->rchild != NULL){
            EnQueue(Q,p->rchild);
        }
    }
}

int main() {
    BiTree pnew; //pnew指向新申请的树结点
    BiTree root = NULL; //root指向树的根结点，代表树
    ptag_t phead = NULL,ptail = NULL,pcur = NULL,listpnew = NULL; //队列头尾指针,pcur当前父结点,listpnew新入队元素

    char c;
    while(scanf("%c",&c)){
        if(c == '\n') break;
        pnew = (BiTree)calloc(1,sizeof(BiTNode)); //calloc申请空间，并初始化为0
        pnew->data = c;
        listpnew = (ptag_t)calloc(1,sizeof(tag_t)); //给队列结点申请空间，并初始化为0
        listpnew->p = pnew;

        if(root == NULL){  //若树为空
            root = pnew;
            phead = ptail = pcur = listpnew;
        }else{ //树非空
            //元素先入队列
            ptail->next = listpnew;  //元素入队
            ptail = listpnew;        //队尾指针后移
            //再加入树中
            if(pcur->p->lchild == NULL){ //若左子树为空，加入左子树
                pcur->p->lchild = pnew;
            }else if(pcur->p->rchild == NULL){ //若右子树为空，加入右子树
                pcur->p->rchild = pnew;
                pcur = pcur->next;
            }
        }
    }
    InOrder(root);
    printf("\n");
    PostOrder(root);
    printf("\n");
    LevelOrder(root);
    printf("\n");
    return 0;
}

15.查找

1.顺序查找（线性查找）

顺序查找又称 线性查找(Linear Search)，它对于顺序表和链表都是适用的。
对于顺序表，可通过数组下标递增来顺序扫描每个元素；对于链表，则通过指针next来依次扫描每个元素。

哨兵

哨兵的作用：提高效率

①传统的顺序查找：

int Search(int array[] , int key ,int len) 
{
	for (int i = 0 ; i < len ; ++i){
		if (array[i] == key)
			return i;
	}
	return -1;
}

②带哨兵的顺序查找：
for循环中少了n次越界判断，提高了一点效率。(如果数据量非常大的话)。
从后往前找。若未找到，一直到a[0]处的哨兵才停滞。正好此时i=0。相当于return 0；

int Search(int array[] , int key ,int len)
{
	array[0] = key;   带哨兵的数组,a[0]不存放数据，存放目标值
	int i;
	for(int i = len-1; array[i] != key; --i);
	return i; // 如果没有找到i = 0，找到 i = 数据所在位置
}

线性查找代码

1.顺序查找(线性查找)代码

int LinearSearch(SSTable ST,int key){
    ST.elem[0] = key;  //key存在0号位置，作为哨兵
    int i;
    for(i = ST.TableLen; ST.elem[i] != key; --i);
    return i;
}

2.完整代码

#include <cstdio>
#include <cstdlib>
#include <ctime>

typedef struct{
    int * elem;   //动态数组,elem指向动态数组的起始地址
    int TableLen; //存储动态数组中元素的个数
}SSTable;

void ST_init(SSTable &ST,int len){
    ST.TableLen = len + 1; //多申请了一个空间，为了0号位置存放哨兵(王道书使用哨兵，不用也行)
    ST.elem = (int*)malloc(sizeof(int) * ST.TableLen);
    int i;
    srand(time(NULL)); //随机数生成
    for(i = 0; i < ST.TableLen; ++i){  //因为0是哨兵，从1开始往后随机
        ST.elem[i] = rand() % 100; //为了让随机生成的数 在0-99之间
    }
}

void ST_print(SSTable ST){
    for(int i = 1; i < ST.TableLen; ++i){ //不打印elem[0]的哨兵
        printf("%d ",ST.elem[i]);
    }
    printf("\n");
}

int LinearSearch(SSTable ST,int key){
    ST.elem[0] = key;  //key存在0号位置，作为哨兵
    int i;
    for(i = ST.TableLen; ST.elem[i] != key; --i);
    return i;
}

//顺序查找
int main() {
    SSTable ST;
    ST_init(ST,10);
    ST_print(ST);

    printf("please input search key:\n");
    int key;
    scanf("%d",&key);

    int pos = LinearSearch(ST,key);
    if(pos){  //if(pos != 0)
        printf("find key,pos=%d\n",pos);
    }else{
        printf("not find.\n");
    }

    return 0;
}

3.顺序查找的时间复杂度：O(n)

2.折半查找（二分查找）

折半查找，又称 二分查找(Binary Search)。仅适用于有序的顺序表。

函数指针

传递一个行为给函数

二分查找代码

1.折半查找(二分查找)代码

int BinarySearch(SSTable ST,int key){
    int low = 0, high = ST.TableLen-1, mid;
    while(low <= high){
        mid = (low + high)/2;
        if(key < ST.elem[mid]){ //key在左边
            high = mid - 1;
        }else if(key > ST.elem[mid]){
            low = mid + 1;
        }else{ // key = ST.elem[mid],恰好找到
            return mid;
        }
    }
    return -1;
}

2.完整代码

#include <cstdio>
#include <cstdlib>
#include <ctime>
#include <algorithm>
using namespace std;

typedef struct{
    int * elem; //申请的堆空间起始地址 //整型指针，申请的堆空间的起始地址存入elem
    int TableLen; //元素个数(表长度)
}SSTable;

void ST_init(SSTable &ST,int len){
    ST.TableLen = len ;
    ST.elem = (int *)malloc(sizeof(int)*ST.TableLen);
    int i;
    srand(time(NULL));
    for(int i = 0; i < ST.TableLen; ++i){
        ST.elem[i] = rand() % 100;
    }
}

void ST_print(SSTable ST){
    for(int i = 0; i < ST.TableLen; ++i){
        printf("%d ",ST.elem[i]);
    }
    printf("\n");
}

int BinarySearch(SSTable ST,int key){
    int low = 0, high = ST.TableLen-1, mid;
    while(low <= high){
        mid = (low + high)/2;
        if(key < ST.elem[mid]){ //key在左边
            high = mid - 1;
        }else if(key > ST.elem[mid]){
            low = mid + 1;
        }else{ // key = ST.elem[mid],恰好找到
            return mid;
        }
    }
    return -1;
}

int main() {
    SSTable ST;
    ST_init(ST,10);
    sort(ST.elem,ST.elem+10); //排序
    ST_print(ST);

    int key;
    printf("please input search key:\n");
    scanf("%d",&key);

    int pos = BinarySearch(ST,key);
    if(pos != -1){
        printf("find key,pos=%d\n",pos);
    }else{
        printf("not find.\n");
    }
    return 0;
}

3.二叉排序树（二叉查找树） BST

BST：二叉排序树(Binary Sort Tree) / 二叉查找树(Binary Search Tree)

BST建树

1.递归建树

//递归地创建二叉排序树
int BST_Insert1(BiTree &T,int k){
    if(T == NULL){
        T = (BiTree)malloc(sizeof(BSTNode));
        T->lchild = T->rchild = NULL;
        T->key = k;
        return 1; //代表插入成功
    }else if(k == T->key) {
        return 0; //相同元素,不插入
    }else if(k < T->key){
        return BST_Insert1(T->lchild,k);
    }else{
        return BST_Insert1(T->rchild,k);
    }
}

void BST_Create(BiTree &T,int str[],int len){
    for(int i = 0; i < len; ++i){          
        BST_Insert1(T,str[i]);
    }
}

2.非递归建树

//非递归地创建二叉排序树
int BST_Insert(BiTree &T,int k){
    BiTree TreeNew = (BiTree)calloc(1,sizeof(BSTNode)); //给新进来的结点申请空间，并初始化，左右孩子为NULL
    TreeNew->key = k;
    if(T == NULL){
        T = TreeNew;
        return 0;
    }

    BiTree p = T,parent; //结点p用来查找新结点的插入位置 ,parent存p的父亲
    while(p){ //p为NULL跳出循环,此时parent为p的父结点
        parent = p;
        if(k < p->key){
            p = p->lchild;
        }else if(k > p->key){  //,向右走
            p = p->rchild;
        }else{ //k == p->key BST中不放相等元素
            return -1; //相同元素
        }
    }

    if(k < parent->key){
        parent->lchild = TreeNew;
    }else{
        parent->rchild = TreeNew;
    }
    return 0;
}

void BST_Create(BiTree &T,int str[],int len){//实参传的是数组str的首地址进来，则形参应该写int* str 或 int str[]
    for(int i = 0; i < len; ++i){           //若实参传的是数组的值str[i],则形参只需要写 int key
        BST_Insert1(T,str[i]);
    }
}

3.查找

//查找是否存在
BiTree BST_Search(BiTree T,int k){
    while(T!=NULL && k!=T->key){ //k == T->key,查找到了目标key,返回结点T。或没查找到,查到了空叶子，返回NULL
        if(k < T->key){
            T = T->lchild;
        }else{
            T = T->rchild;
        }
    }
    return T;
}

4.删除
分三种情况：左子树为空、右子树为空、左右子树均不为空

//递归删除BST结点
void BST_DeleteNode(BiTree &root,int x){
    if(root == NULL){
        return;
    }else if(root->key > x){ //根结点比要找的值大,去左子树找
        BST_DeleteNode(root->lchild,x);
    }else if(root->key < x){  //根结点比要找的值小,去右子树找
        BST_DeleteNode(root->rchild,x);
    }else{ //相等,找到了要删除的结点
        if(root->lchild==NULL){    //1.左子树为空
            BiTree tempNode = root;
            root = root->rchild; //右孩子顶上去
            free(tempNode);
        }else if(root->rchild==NULL){  //2.右子树为空
            BiTree tempNode = root;
            root = root->lchild; //左孩子顶上去
            free(tempNode);
        }else{  //3.左右子树都不为空
            BiTree tempNode = root->lchild;
            while(tempNode->rchild){ //找到左子树的最大结点(最右结点)，把值赋给该结点，把赋值结点删除。
                tempNode = tempNode->rchild;
            }
            root->key = tempNode->key;
//            free(tempNode); //不能直接删除，可能有孩子结点
            BST_DeleteNode(root->lchild,tempNode->key);
        }
    }
}

5.完整代码：建树、中序遍历、查找、删除

#include <cstdio>
#include <cstdlib>

typedef struct BSTNode{
    int key;
    struct BSTNode *lchild,*rchild;
}BSTNode,*BiTree;

//递归地创建二叉排序树:插入
int BST_Insert1(BiTree &T,int k){
    if(T == NULL){
        T = (BiTree)malloc(sizeof(BSTNode));
        T->key = k;        
        T->lchild = T->rchild = NULL;
        return 1; //代表插入成功
    }else if(k == T->key) {
        return 0; //相同元素,不插入
    }else if(k < T->key){
        return BST_Insert1(T->lchild,k);
    }else{
        return BST_Insert1(T->rchild,k);
    }
}

//非递归地创建二叉排序树:插入
int BST_Insert(BiTree &T,int k){
    BiTree TreeNew = (BiTree)calloc(1,sizeof(BSTNode)); //给新进来的结点申请空间，并初始化，左右孩子为NULL
    TreeNew->key = k;
    if(T == NULL){
        T = TreeNew;
        return 0;
    }

    BiTree p = T,parent; //结点p用来查找新结点的插入位置 ,parent存p的父亲
    while(p){ //p为NULL跳出循环,此时parent为p的父结点
        parent = p;
        if(k < p->key){
            p = p->lchild;
        }else if(k > p->key){  //,向右走
            p = p->rchild;
        }else{ //k == p->key BST中不放相等元素
            return -1; //相同元素
        }
    }

    if(k < parent->key){
        parent->lchild = TreeNew;
    }else{
        parent->rchild = TreeNew;
    }
    return 0;
}

void BST_Create(BiTree &T,int str[],int len){//实参传的是数组str的首地址进来，则形参应该写int* str 或 int str[]
    for(int i = 0; i < len; ++i){           //若实参传的是数组的值str[i],则形参只需要写 int key
        BST_Insert1(T,str[i]);
    }
}

//中序遍历,左根右
void InOrder(BiTree T){
    if(T != NULL){
        InOrder(T->lchild);
        printf("%d ",T->key);
        InOrder(T->rchild);
    }
}
/*
BiTree BST_Search(BiTree T,int k,BiTree &parent){ //万一要求对父亲操作,这里保存了parent,但是没用上
    parent = NULL;
    while(T!=NULL && k!=T->key){
        parent = T;
        if(k < T->key){
            T = T->lchild;
        }else{
            T = T->rchild;
        }
    }
    return T;
}*/

//查找是否存在
BiTree BST_Search(BiTree T,int k){
    while(T!=NULL && k!=T->key){ //k == T->key,查找到了目标key,返回结点T。或没查找到,查到了空叶子，返回NULL
        if(k < T->key){
            T = T->lchild;
        }else{
            T = T->rchild;
        }
    }
    return T;
}

//递归删除BST结点
void BST_DeleteNode(BiTree &root,int x){
    if(root == NULL){
        return;
    }else if(root->key > x){ //根结点比要找的值大,去左子树找
        BST_DeleteNode(root->lchild,x);
    }else if(root->key < x){  //根结点比要找的值小,去右子树找
        BST_DeleteNode(root->rchild,x);
    }else{ //相等,找到了要删除的结点
        if(root->lchild==NULL){  //左子树为空
            BiTree tempNode = root;
            root = root->rchild; //右孩子顶上去
            free(tempNode);
        }else if(root->rchild==NULL){  //右子树为空
            BiTree tempNode = root;
            root = root->lchild; //左孩子顶上去
            free(tempNode);
        }else{ //左右子树都不为空
            BiTree tempNode = root->lchild;
            while(tempNode->rchild){ //找到左子树的最大结点(最右结点)，把值赋给该结点，把赋值结点删除。
                tempNode = tempNode->rchild;
            }
            root->key = tempNode->key;
//            free(tempNode); //不能直接删除，可能有孩子结点
            BST_DeleteNode(root->lchild,tempNode->key);
        }
    }

}

//二叉排序树:建树,中序遍历,查找
int main() {
    BiTree T = NULL; //树根
    int str[7] = {54,20,66,40,28,79,58};
    BST_Create(T,str,7);
    InOrder(T);
    printf("\n");

//    BiTree search,parent;
//    search = BST_Search(T,40,parent);
    BiTree search = BST_Search(T,58);
    if(search){
        printf("find key = %d\n",search->key);
    }else{
        printf("not find.\n");
    }

    BST_DeleteNode(T,999);
    InOrder(T);
    printf("\n");
    return 0;
}

16.17.18.排序

排序分为：
(1)交换排序：冒泡排序、快速排序
(2)插入排序：直接插入排序、折半插入排序、希尔排序
(3)选择排序：简单选择排序、堆排序
(4)归并排序

1.冒泡排序

1.算法思想：从后往前，将最小元素冒到最前面去。n-1趟，每趟对比n-i次

2.时间复杂度：
①最好：O(n) 【已经有序，外层循环n次】
②平均：O(n²) 【外层n次*内层n次 = n²次】
③最坏：O(n²)

空间复杂度：O(1)

3.核心代码：

void swap(int &a,int &b){
    int temp = a;
    a = b;
    b = temp;
}

void BubbleSort(int* A,int n){ //长度为n
    for(int i = 0; i < n-1; ++i){ //n-1趟:0~n-2
    	bool flag = false;
        for(int j = n-1; j > i; --j){
            if(A[j-1]>A[j]){ //从后向前冒
                swap(A[j-1],A[j]);
                flag = true;
            }
        }
        if(flag==false) return; //优化:若已经有序，则直接返回。
    }
}

4.完整可运行代码：

#include <cstdio>
#include <cstdlib>
#include <ctime>

typedef struct{
    int * elem; //存储元素的起始地址
    int TableLen; //顺序表中元素个数
}SSTable;

void ST_init(SSTable &ST,int len){
    ST.TableLen = len;
    ST.elem = (int*)malloc(sizeof(int) * ST.TableLen);
    srand(time(NULL)); //随机数生成
    for(int i = 0; i < ST.TableLen; ++i){  //因为0是哨兵，从1开始往后随机
        ST.elem[i] = rand() % 100; //为了让随机生成的数 在0-99之间
    }
}

void ST_print(SSTable ST){
    for(int i = 0; i < ST.TableLen; ++i){
        printf("%d ",ST.elem[i]);
    }
    printf("\n");
}

void swap(int &a,int &b){
    int temp = a;
    a = b;
    b = temp;
}

void BubbleSort(int* A,int n){ //长度为n
    for(int i = 0; i < n-1; ++i){ //0~n-2,共n-1趟
    	bool flag = false; //每一趟，重置flag为false，因此放到外层i循环的里面
        for(int j = n-1; j > i; --j){ //从后向前冒
            if(A[j-1]>A[j]){ 
                swap(A[j-1],A[j]);
                flag = true;
            }
        }
        if(flag==false) return; //优化:若已经有序，则直接返回。
    }
}

int main() {
    SSTable ST;
    ST_init(ST,10);
    ST_print(ST);

    BubbleSort(ST.elem,10);
    ST_print(ST);
    return 0;
}

2.快速排序

1.算法思想：分治。
①快速排序的实现：QuickSort
拿数组第一个元素作为分割值，比分割值小的放在其左边，比分割值大的放在其右边，这样就确定了分割值在原数组中的位置，以及产生了左右两个更小的数组。递归地对左右两个数组再进行快速排序，直至每个小数组只有一个元素。此时整个大数组就有序了。

②分割 —— “比分割值小的放在其左边，比分割值大的放在其右边”的实现：Partition
(1)动画网站交换法：设置两个值i,j。分别指向第2个元素和最后一个元素。 $i + +, j - -$ 。直到找到 $A [i] > A [0], A [j] < A [0]$ ，交换i和j所指元素。继续每轮i加j减。碰到不符合的停下指针，i,j都停下就交换。
直到j<i，将A[0]和A[j]交换位置。

(2)王道挖坑法：
先用pivot把A[low]存起来。这样数组里就多了一个可以用的坑。
直接不断high–，直到找到了比pivot小的值，直接将其覆盖到A[low]。 ①
然后不断low++，直到碰到了pivot大的值，直接复制到刚才high的位置。②
重复①②，直到low==high，将pivot放到Ahigh处。完成分割。

2.时间复杂度：
①最好：O(nlog₂n) 【Partition中while里的两个小while之和走了n次。QuickSort走log₂n次】
②平均：O(nlog₂n)
③最差：O(n²) 【每次QuickSort接收的中枢值都在最左/右边上，QuickSort下降为n，退化为O(n²)】

空间复杂度：O(log₂n) 【QuickSort递归次数是log₂n次，每次递归形参都要占用空间。int low,int high共8个字节】

3.核心代码：

//分割函数 【挖坑法】
int Partition(int A[],int low,int high){
    int pivot = A[low];
    while(low<high){
        while(low<high&&A[high]>=pivot) --high;  //相等时也要移动，否则会死循环
        A[low] = A[high];
        while(low<high&&A[low]<=pivot) ++low;   //相等时也要移动，否则会死循环
        A[high] = A[low];
    }				  //到达目标位置，把之前的旧A[low]从pivot里取出来
    A[low] = pivot;   //此时low和high同位置。或者 A[high] = pivot;
    return low;       //                       return high;
}

void QuickSort(int A[],int low,int high){
    if(low < high){ //递归出口
        int pivotpos = Partition(A, low, high);
        QuickSort(A,low,pivotpos-1);  //前一半递归快排
        QuickSort(A,pivotpos+1,high); //后一半递归快排
    }
}

4.完整可执行代码：

#include <cstdio>
#include <cstdlib>
#include <ctime>


void PrintArray(int *A){
    for(int i = 0; i <= 9; ++i){
        printf("%d ",A[i]);
    }
    printf("\n");
}

//挖坑法
int Partition(int A[],int low,int high){
    int pivot = A[low];
    while(low<high){
        while(low<high&&A[high]>=pivot) high--;  //相等时也要移动，否则会死循环
        A[low] = A[high];
        while(low<high&&A[low]<=pivot) low++;   //相等时也要移动，否则会死循环
        A[high] = A[low];
    }
    A[low] = pivot;   //此时low和high同位置。或者 A[high] = pivot;
    return low;       //                       return high;
}

void QuickSort(int A[],int low,int high){
    if(low < high){ //至少要两个元素  low < high,方便递归。
        int pivotpos = Partition(A, low, high);
        QuickSort(A,low,pivotpos-1);  //前一半递归快排
        QuickSort(A,pivotpos+1,high); //后一半递归快排
    }
}

int main(){
    int A[10] = {10,10,8,7,6,5,4,3,2,1};
//    srand(time(NULL));
//    int A[10];
//    for(int i = 0; i < 10; ++i){
//        A[i] = rand()%100;
//    }
    PrintArray(A);
    QuickSort(A,0,9);
    PrintArray(A);
    return 0;
}

随机数生成

①头文件：<cstdlib>、<ctime>

②初始化：srand(time(NULL));

③随机数函数：rand()

④完整代码：

#include <cstdlib>
#include <ctime>

srand(time(NULL));
int A[10];
for(int i = 0; i < 10; ++i){
	A[i] = rand()%100;
}

3.直接插入排序

1.算法思想：前面是有序序列，分界线后面是无序序列。
(挖坑法) 先用变量insertval保存无序序列第一个元素，将之与有序序列的最后一个元素对比大小，若其比insertval大，则覆盖无序序列第第一个元素位置，大的覆盖小的，覆盖后一个。再继续向前比。
insertval与有序序列倒数第二个元素对比。大的那个元素把坑填上。 直至找到合适的位置。

挖坑法：用一个变量保存第一个值，造成一个坑，后面元素直接覆盖。效率高于交换swap。本质属于交换排序的优化。

2.适用场景：
手机通讯录 (原本有序)，新增了一个联系人。使用插入排序。

3.时间复杂度：
①最好：O(n) 【已经有序，遍历一遍即可。不发生覆盖】
②平均：O(n²)
③最坏：O(n²)

4.核心代码：

void InsertSort(int A[],int n){
    int i,j,insertval;
    for(i = 1; i < n; ++i){ //n-1趟:1~n-1
        insertval = A[i];
        for(j = i-1; j>=0 && A[j]>insertval; --j){ 
                A[j+1] = A[j];  //向后覆盖            
        }
        A[j+1] = insertval;
    }
}

把if(A[j] > insertval)拆到for循环的判断里。能在定位到插入位置后就停下。减少了循环次数。
否则，按原来方式，就算找到了插入位置。循环也会持续进行到j<0为止。

5.完整可运行代码：

#include <cstdio>

void PrintArray(int A[]){
    for(int i = 0; i < 10; ++i){
        printf("%d ",A[i]);
    }
    printf("\n");
}

void InsertSort(int A[],int n){
    int i,j,insertval;
    for(i = 1; i < n; ++i){
         insertval = A[i];
        for(j = i-1; j>=0 && A[j]>insertval; --j){ 
                A[j+1] = A[j];  //向后覆盖            
        }
        A[j+1] = insertval;
    }
}

int main() {
    int A[10] = {10,9,8,7,6,5,4,3,2,1};
    PrintArray(A);
    InsertSort(A,10);
    PrintArray(A);
    return 0;
}

16OJ

#include <cstdio>
#include <cstring>
#include <cstdlib>

typedef struct{
    int * elem; //存储元素的起始地址
    int TableLen; //顺序表中元素个数
}SSTable;

void ST_init(SSTable &ST,int len){
    ST.TableLen = len;
    ST.elem = (int*)malloc(sizeof(int) * ST.TableLen);
}

void ST_print(SSTable ST){
    for(int i = 0; i < ST.TableLen; ++i){
        printf("%3d",ST.elem[i]);
    }
}

void PrintArray(int A[]){
    for(int i = 0; i < 10; ++i){
        printf("%3d",A[i]);
    }
}

void swap(int &a,int &b){
    int temp = a;
    a = b;
    b = temp;
}

void BubbleSort(int A[],int n){ //10 9 8 7 6 5 4 3 2 1
    for(int i = 0; i < n; ++i){
    	bool flag = false;
        for(int j = n-1; j > i; --j){
            if(A[j-1]>A[j]){
                swap(A[j-1],A[j]);
                flag = true;
            }
        }
        if(flag==false) return;
    }
}

int Partition(int A[],int low,int high){
    int pivot = A[low];
    while(low<high){
        while(low<high&&A[high]>=pivot) high--;
        A[low] = A[high];
        while(low<high&&A[low]<=pivot) low++;
        A[high] = A[low];
    }
    A[low] = pivot;
    return low;
}

void QuickSort(int A[],int low,int high){
    if(low<high){ //递归出口
        int pivotpos = Partition(A,low,high);
        QuickSort(A,low,pivotpos-1);
        QuickSort(A,pivotpos+1,high);
    }
}

void InsertSort(int A[],int n){
    int i,j,insertval;
    for(i = 1; i < n; ++i){ //n-1趟:1~n-1
        insertval = A[i]; //挖坑
        for(j = i-1; j>=0 && A[j]>insertval; --j){
            A[j+1] = A[j];
        }
        A[j+1] = insertval;
    }
}

int main() {
    int A[10],B[10],C[10];
    for(int i = 0; i < 10; ++i){
        scanf("%d",&A[i]);
    }
    memcpy(B,A,40);
    memcpy(C,A,40);

    BubbleSort(A,10);
    PrintArray(A);
    printf("\n");
    QuickSort(B,0,9);
    PrintArray(B);
    printf("\n");
    InsertSort(C,10);
    PrintArray(C);


//    SSTable ST;
//    ST_init(ST,10);
//    int A[10];
//    for(int i = 0; i < 10; ++i){
//        scanf("%d",&A[i]);
//    }
//    memcpy(ST.elem,A,sizeof(A));
    ST_print(ST);
//    BubbleSort(ST.elem,10);
//    ST_print(ST);
//    printf("\n");
//    memcpy(ST.elem,A,sizeof(A));
    ST_print(ST);
//    QuickSort(ST.elem,0,9);
//    ST_print(ST);
//    printf("\n");
//    memcpy(ST.elem,A,sizeof(A));
    ST_print(ST);
//    InsertSort(ST.elem,10);
//    ST_print(ST);
    return 0;
}

4.(简单)选择排序

1.算法思想：遍历n-1趟，每趟记录最小值的下标，与当前无序序列第一个元素进行交换。

2.特点：每趟可确定一个最值的最终位置

3.时间复杂度：最好、平均、最坏均为O(n²)
空间复杂度：O(1)

4.核心代码：

void SelectionSort(int A[],int n){
    int i,j,min;//min记录最小值的下标
    for(i = 0; i < n-1; ++i){
        min = i;
        for(j = i+1; j < n; ++j){
            if(A[j] < A[min]){
                min = j;
            }
        }
        swap(A[i],A[min]);
    }
}

5.完整可运行代码：

#include <cstdio>
#include <cstdlib>
#include <ctime>

typedef struct{
    int * elem; //存储元素的起始地址
    int TableLen; //顺序表中元素个数
}SSTable;

void ST_init(SSTable &ST,int len){
    ST.TableLen = len;
    ST.elem = (int*)malloc(sizeof(int) * ST.TableLen);
    srand(time(NULL)); //随机数生成
    for(int i = 0; i < ST.TableLen; ++i){  //因为0是哨兵，从1开始往后随机
        ST.elem[i] = rand() % 100; //为了让随机生成的数 在0-99之间
    }
}

void ST_print(SSTable ST){
    for(int i = 0; i < ST.TableLen; ++i){
        printf("%d ",ST.elem[i]);
    }
    printf("\n");
}

void swap(int &a,int &b){
    int temp = a;
    a = b;
    b = temp;
}

void SelectionSort(int *A,int n){
    int min;//min记录最小值的下标
    for(int i = 0; i < n-1; ++i){
        min = i;
        for(int j=i+1; j < n; ++j){
            if(A[j] < A[min]){
                min = j;
            }
        }
        swap(A[i],A[min]);
    }
}


int main() {
    SSTable ST;
    ST_init(ST,10);
    ST_print(ST);
    SelectionSort(ST.elem,10);
    ST_print(ST);
    return 0;
}

5.堆排序

1.算法思想(原理)：
①将数组在逻辑上顺序存储为完全二叉树。
从最后一个父结点开始，左右孩子中大的一个与父结点比较，若孩子大则交换。旧父结点交换下去后要再跟新的左右孩子比大小，若小则继续下坠。
②倒数第二个父结点，继续重复①。直至根结点也完成了①。则选出了最大值作为根结点。这称为完成了一趟。
③直接输出根结点，或根结点与最后一个结点swap，下一趟选最大值从剩余的n-1个元素中进行。直至进行n-1趟。整个数组也就排好序了。

大根堆：父结点比左右孩子结点都大
小根堆：父结点比左右孩子结点都小
若父结点下标为i(从0开始)，则左孩子结点下标为2*i+1

2.时间复杂度：O(nlog₂n)
空间复杂度：O(1) 【没有递归，也没有额外使用数组】

3.核心代码：

//将当前子树调整为大根堆 【将i号结点的子树调整为大根堆,堆总结点数为n】
void HeadAdjust(int A[],int i,int n){
    int dad = i;
    int son = 2*i+1;
    while(son < n){
        if(son+1<n && A[son]<A[son+1]){
            son++;
        }
        if(A[dad] < A[son]){ //此时的A[son]为左右孩子中大的那个
            swap(A[dad],A[son]);
            dad = son;
            son = 2*dad + 1;  //新父亲的儿子。下坠调整。while执行 O(log₂n)次
        }else{ //父亲大，则不需要调整，直接结束
            break;
        }
    }
}

void HeapSort(int A[],int n){
	//建立大根堆
    for(int i = n/2-1; i >= 0; --i){    //第一个for循环执行了n/2次
        HeadAdjust(A,i,n);
    }
    swap(A[0],A[n-1]);  //将最大值与最后一个元素交换
    //反复对根结点建立大根堆，然后调整至堆尾
    for(int i = n-1; i > 1 ;--i){     //第二个for循环执行了n-2次。因此时间复杂度为O(nlog₂n)
        HeadAdjust(A,0,i); //现在只需要调整根结点子树为大根堆
        swap(A[0],A[i-1]);
    }
}

4.完整可执行代码：

#include <cstdio>
#include <cstdlib>
#include <ctime>
#include <cstring>

typedef struct{
    int * elem; //存储元素的起始地址
    int TableLen; //顺序表中元素个数
}SSTable;

void ST_init(SSTable &ST,int len){
    ST.TableLen = len;
    ST.elem = (int*)malloc(sizeof(int) * ST.TableLen);
    srand(time(NULL)); //随机数生成
    for(int i = 0; i < ST.TableLen; ++i){  //因为0是哨兵，从1开始往后随机
        ST.elem[i] = rand() % 100; //为了让随机生成的数 在0-99之间
    }
}

void ST_print(SSTable ST){
    for(int i = 0; i < ST.TableLen; ++i){
        printf("%d ",ST.elem[i]);
    }
    printf("\n");
}

void swap(int &a,int &b){
    int temp = a;
    a = b;
    b = temp;
}

//将当前子树调整为大根堆
void HeadAdjust(int A[],int i,int n){
    int dad = i;
    int son = 2*i+1;
    while(son < n){
        if(son+1<n && A[son]<A[son+1]){
            son++;
        }
        if(A[son]>A[dad]){ //此时的A[son]为左右孩子中大的那个
            swap(A[son],A[dad]);
            dad = son;
            son = 2*dad + 1;  //新父亲的儿子。下坠调整。while执行 O(log₂n)次
        }else{ //父亲大，则不需要调整，直接结束
            break;
        }
    }
}

void HeapSort(int A[],int n){
    for(int i = n/2-1; i >= 0; --i){    //第一个for循环执行了n/2次
        HeadAdjust(A,i,n);
    }
    swap(A[0],A[n-1]);
    for(int i = n-1; i > 1 ;--i){     //第二个for循环执行了n-2次。因此时间复杂度为O(nlog₂n)
        HeadAdjust(A,0,i); //现在只需要调整根结点子树为大根堆
        swap(A[0],A[i-1]);
    }
}

int main() {
    SSTable ST;
    ST_init(ST,10);
//    int A[10] = {3,87,2,93,78,56,61,38,12,40};
//    memcpy(ST.elem,A,sizeof(A));
    ST_print(ST);
    HeapSort(ST.elem,10);
    ST_print(ST);
    return 0;
}

6.归并排序

1.算法思想：2路归并排序，相邻的两两一组进行归并排序。然后下一趟再相邻的两两一组进行归并排序。【归并排序和快速排序，考研只要掌握<递归实现>即可】
在这里插入图片描述

在这里插入图片描述

2.时间复杂度：O(nlog₂n)
空间复杂度：O(n)

3.核心代码：

//合并两个有序数组 【两个for加起来共执行了n次】
int *B = new int[n]; 

//A[low,mid]和A[mid+1,high]各自有序，将这两部分合并
void Merge(int A[],int low,int mid,int high){
    int i,j,k;
    for(i = low; i <= high; ++i){
        B[i] = A[i];
    }
    for(i = low,j = mid+1,k = low; i<=mid&&j<=high; k++){  //合并两个有序数组
        if(B[i] <= B[j]){  //<=,优先选i,稳定性
            A[k] = B[i];  //小的放前面，顺序排序
            i++;
        }else{
            A[k] = B[j];
            j++;
        }
    }
    while(i <= mid){
        A[k] = B[i];
        i++;
        k++;
    }
    while(j <= high){
        A[k] = B[j];
        j++;
        k++;
    }
}

//归并排序(递归实现) 【执行了log₂n次】
void MergeSort(int A[],int low,int high){
    if(low<high){ //递归出口
        int mid = (low+high)/2;   //中间划分
        MergeSort(A,low,mid);     //左半部分(递归)归并排序
        MergeSort(A,mid+1,high);  //右半部分(递归)归并排序
        Merge(A,low,mid,high);    //归并排序
    }
}

4.完整可运行代码：

#include <cstdio>
#include <cstdlib>

void PrintArray(int A[]){
    for(int i = 0; i < 10; ++i){
        printf("%d ",A[i]);
    }
    printf("\n");
}

//合并两个有序数组
void Merge(int A[],int low,int mid,int high){
    static int B[10]; //加static的目的是，无论递归调用多少次，都申请一个数组
    int i,j,k;
    for(i = low; i <= high; ++i){
        B[i] = A[i];
    }
    for(i = low,j = mid+1,k = low; i<=mid && j<=high; k++){  //合并两个有序数组
        if(B[i] < B[j]){
            A[k] = B[i++];  //小的放前面，顺序排序
        }else{
            A[k] = B[j++];
        }
    }
    while(i <= mid)   A[k++] = B[i++];
    while(j <= high)  A[k++] = B[j++];
}

//归并排序(递归实现)
void MergeSort(int A[],int low,int high){
    if(low<high){ //递归出口
        int mid = (low+high)/2;
        MergeSort(A,low,mid);
        MergeSort(A,mid+1,high);
        Merge(A,low,mid,high);
    }
}

int main() {
    int A[10] = {10,9,8,7,6,5,4,3,2,1};
    PrintArray(A);
    MergeSort(A,0,9);
    PrintArray(A);
    return 0;
}