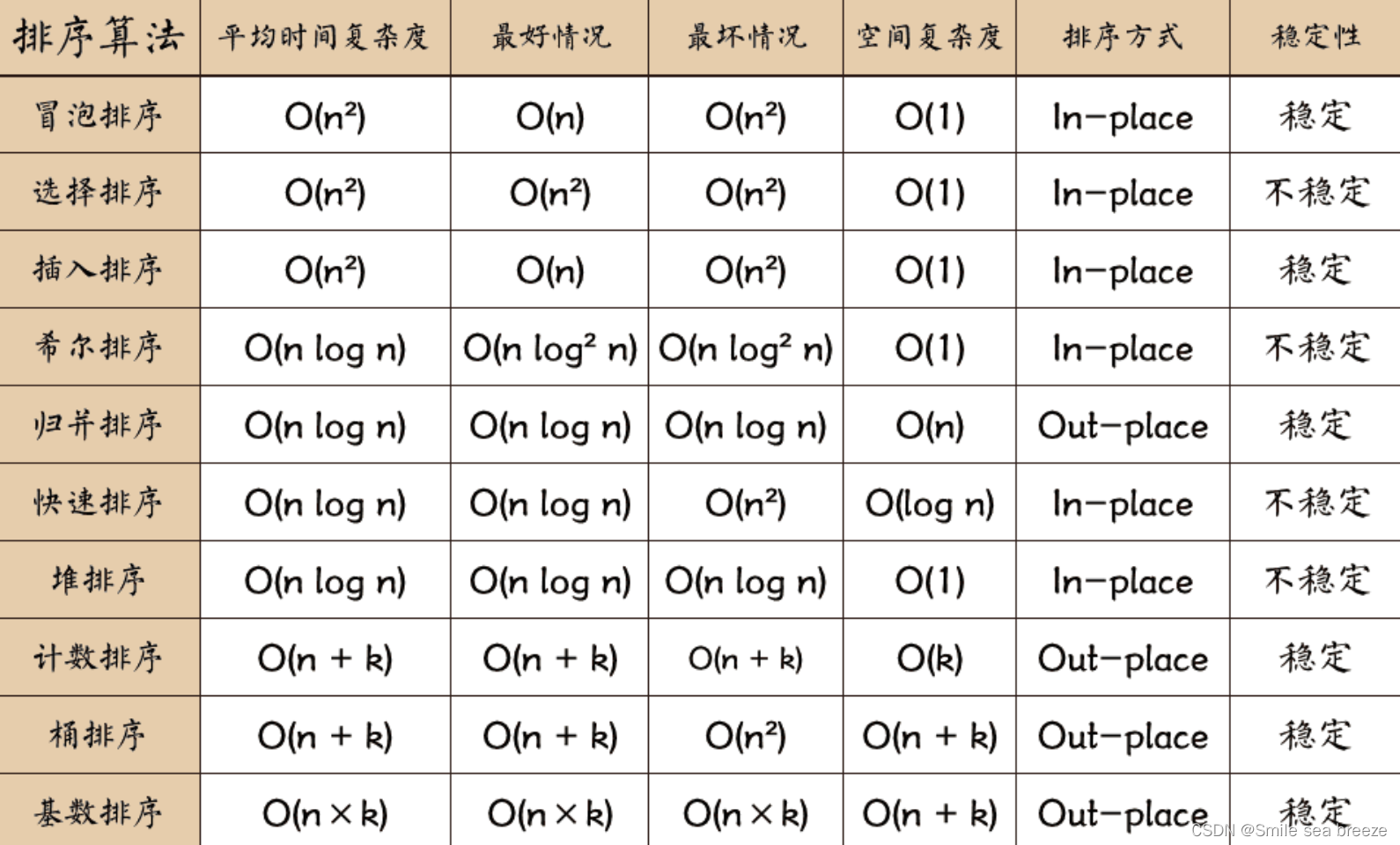
排序算法
排序算法可以分为内部排序和外部排序
内部排序是数据记录在内存中进行排序
外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。常见的内部排序算法有:插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。
关于时间复杂度
平方阶 (O(n2)) 排序 各类简单排序:直接插入、直接选择和冒泡排序。
线性对数阶 (O(nlog2n)) 排序 快速排序、堆排序和归并排序;
O(n1+§)) 排序,§ 是介于 0 和 1 之间的常数。 希尔排序
线性阶 (O(n)) 排序 基数排序,此外还有桶、箱排序。
关于稳定性
稳定的排序算法:冒泡排序、插入排序、归并排序和基数排序。
不是稳定的排序算法:选择排序、快速排序、希尔排序、堆排序。
名词解释:
n:数据规模
k:"桶"的个数
In-place:占用常数内存,不占用额外内存
Out-place:占用额外内存
稳定性:排序后 2 个相等键值的顺序和排序之前它们的顺序相同
1.冒泡排序
public class BubbleSort {
public static void main(String[] args) {
int[] array = {5,9,7,4,1,3,2,8};
bubble(array);
}
public static void bubble(int[] array){
for (int j = 0; j < array.length - 1; j++) {
//一轮冒泡
boolean swapped = false; //表示是否发生了交换 false表示没有发生交换
for (int i = 0; i < array.length - 1 - j; i++) {
if (array[i] > array[i+1]) {
swap(array, i, i+1);
swapped = true;
}
}
if (!swapped) {//数组中的元素没有发生交换,直接退出循环
break;
}
System.out.println("第"+(j+1)+"轮冒泡:"+ Arrays.toString(array));
}
}
public static void swap(int[] array,int i,int j){//将数组中下标为i和j的元素分别交换位置
int t = array[i]; //先将下标为 i 的元素取出来放进缓存区
array[i] = array[j];//将下标为 j 的元素放到原先下标为 i 的位置
array[j] = t; //将下标为 i 的元素 从缓存区里取出来放入 原先下标为 j 的位置
}
}
[5, 7, 4, 1, 3, 2, 8, 9]
[5, 4, 1, 3, 2, 7, 8, 9]
[4, 1, 3, 2, 5, 7, 8, 9]
[1, 3, 2, 4, 5, 7, 8, 9]
[1, 2, 3, 4, 5, 7, 8, 9]
[1, 2, 3, 4, 5, 7, 8, 9]
2.选择排序
public class SelectionSort {
public static void main(String[] args) {
int[] array = {5,3,7,2,1,9,8,4};
selection(array);
}
private static void selection(int[] array){
for (int i = 0; i < array.length - 1; i++) {//i 代表每轮选择最小元素要交换到的目标索引
int minIndex = i; // 代表最小元素的索引
for (int j = minIndex + 1; j < array.length; j++) { //假定下标为 0 的元素为最小,所以循环次数为数组的长度
if (array[minIndex] > array[j]) {
minIndex = j; //更新最小下标
}
}
if (minIndex != i) { //如果最小下标发生变化,则更换元素的位置
swap(array, minIndex, i);
}
System.out.println(Arrays.toString(array));
}
}
public static void swap(int[] array,int i,int j){//将数组中下标为i和j的元素分别交换位置
int t = array[i]; //先将下标为 i 的元素取出来放进缓存区
array[i] = array[j];//将下标为 j 的元素放到原先下标为 i 的位置
array[j] = t; //将下标为 i 的元素 从缓存区里取出来放入 原先下标为 j 的位置
}
}
[1, 3, 7, 2, 5, 9, 8, 4]
[1, 2, 7, 3, 5, 9, 8, 4]
[1, 2, 3, 7, 5, 9, 8, 4]
[1, 2, 3, 4, 5, 9, 8, 7]
[1, 2, 3, 4, 5, 9, 8, 7]
[1, 2, 3, 4, 5, 7, 8, 9]
[1, 2, 3, 4, 5, 7, 8, 9]
3.插入排序
public class InsertSort {
public static void main(String[] args) {
int[] array = {9,3,7,2,5,8,1,4};
insert(array);
}
private static void insert(int[] array){
for (int i = 1; i < array.length; i++) {//i 表示待插入元素的索引
int t = array[i]; //表示待插入的元素值
int j = i - 1; //表示已将排序区域的元素索引
while (j >= 0) {
if (t < array[j]) {//待插入的元素值 小于 已将排序区域的元素索引的值
array[j+1] = array[j];//将下标为 j 的元素向后移动一位
}else { //待插入的元素值 大于 已经排序区域的元素索引的值
break; //找到插入位置,直接退出循环
}
j--; //依次向前进行比较,直到下标出现为负,退出循环
}
array[j+1] = t;//将待插入的元素值 插入到 空出的位置
System.out.println(Arrays.toString(array));
}
}
}
[9, 3, 7, 2, 5, 8, 1, 4]
[3, 9, 7, 2, 5, 8, 1, 4]
[3, 7, 9, 2, 5, 8, 1, 4]
[2, 3, 7, 9, 5, 8, 1, 4]
[2, 3, 5, 7, 9, 8, 1, 4]
[2, 3, 5, 7, 8, 9, 1, 4]
[1, 2, 3, 5, 7, 8, 9, 4]
[1, 2, 3, 4, 5, 7, 8, 9]
4.希尔排序
package practise;
import java.util.Arrays;
public class ShellSort {
public static void main(String[] args) {
int[] array = {9, 3, 7, 2, 5, 8, 1, 4};
shell(array);
}
private static void shell(int[] arr) {
int length = arr.length;
int temp;
for (int step = length / 2; step >= 1; step /= 2) {
for (int i = step; i < length; i++) {
temp = arr[i];
int j = i - step;
while (j >= 0 && arr[j] > temp) {
arr[j + step] = arr[j];
j -= step;
}
arr[j + step] = temp;
System.out.println(Arrays.toString(arr));
}
}
}
}
[5, 3, 7, 2, 9, 8, 1, 4]
[5, 3, 7, 2, 9, 8, 1, 4]
[5, 3, 1, 2, 9, 8, 7, 4]
[5, 3, 1, 2, 9, 8, 7, 4]
[1, 3, 5, 2, 9, 8, 7, 4]
[1, 2, 5, 3, 9, 8, 7, 4]
[1, 2, 5, 3, 9, 8, 7, 4]
[1, 2, 5, 3, 9, 8, 7, 4]
[1, 2, 5, 3, 7, 8, 9, 4]
[1, 2, 5, 3, 7, 4, 9, 8]
[1, 2, 5, 3, 7, 4, 9, 8]
[1, 2, 5, 3, 7, 4, 9, 8]
[1, 2, 3, 5, 7, 4, 9, 8]
[1, 2, 3, 5, 7, 4, 9, 8]
[1, 2, 3, 4, 5, 7, 9, 8]
[1, 2, 3, 4, 5, 7, 9, 8]
[1, 2, 3, 4, 5, 7, 8, 9]
5. 快速排序
5.1单边循环快排
public class QuickSort1 {
public static void main(String[] args) {
int[] array = {5,3,7,2,9,8,1,4};
//3,5,7,2,9,8,1,4 3,2,7,5,9,8,1,4 3,2,1,5,9,8,7,4 3,2,1,4,9,8,7,5
//3,2,1,4,9,8,7,5 1,2,3,4,9,8,7,5 1,2,3,4,5,8,7,9 1,2,3,4,5,7,8,9
quick(array, 0, array.length-1);
}
//递归
public static void quick(int[] array,int low,int high){
if (low >= high) {
return;
}
int p = partition(array, low, high); //表示 基准点元素所在的正确索引
//确定左边分区范围
quick(array,low,p-1);
//确定右边分区范围
quick(array, p+1, high);
}
//分区
private static int partition(int[] array,int low,int high){ //low 表示左边界 high: 表示右边界
int pv = array[high]; //选取最右边的元素为基准点元素
int i = low;
for (int j = low; j < high; j++) {
if (array[j] < pv) {//下标小于基准点的元素
swap(array, i, j); //将小于基准点的元素换到 下标为i 所在的位置
i++;
}
}
swap(array, high, i); //将基准点和 下标为i 的元素互换位置
System.out.println(Arrays.toString(array)+"i="+i);
//返回值表示基准点元素所在的正确索引,以此来确定下一轮的边界分区
return i;
}
public static void swap(int[] array,int i,int j){//将数组中下标为i和j的元素分别交换位置
int t = array[i]; //先将下标为 i 的元素取出来放进缓存区
array[i] = array[j];//将下标为 j 的元素放到原先下标为 i 的位置
array[j] = t; //将下标为 i 的元素 从缓存区里取出来放入 原先下标为 j 的位置
}
}
[3, 2, 1, 4, 9, 8, 7, 5]i=3
[1, 2, 3, 4, 9, 8, 7, 5]i=0
[1, 2, 3, 4, 9, 8, 7, 5]i=2
[1, 2, 3, 4, 5, 8, 7, 9]i=4
[1, 2, 3, 4, 5, 8, 7, 9]i=7
[1, 2, 3, 4, 5, 7, 8, 9]i=5
5.2双边循环快排
public class QuickSort2 {
public static void main(String[] args) {
int[] array = {5,3,7,2,9,8,1,4};
// 5,3,4,2,9,8,1,7 5,3,4,2,1,8,9,7 1,3,4,2,5,8,9,7
// 1,3,2,4,5,8,9,7 1,2,3,4,5,8,9,7 1,2,3,4,5,8,7,9 1,2,3,4,5,7,8,9
quick(array, 0, array.length-1);
}
//递归
public static void quick(int[] array,int low,int high){
if (low >= high) {
return;
}
int p = partition(array, low, high); //表示 基准点元素所在的正确索引
//确定左边分区范围
quick(array,low,p-1);
//确定右边分区范围
quick(array, p+1, high);
}
//分区
private static int partition(int[] array,int low,int high){ //low 表示左边界 high: 表示右边界
int pv = array[low]; //选取最左边的元素为基准点元素
int i = low; //i 开始位于左边界
int j = high; // j 开位于右边界
while (i < j){
//j 从最右边的元素开始找 小于基准点的元素
while (i < j && array[j] > pv) { // i < j -- 防止 i 和 j发生越界
j--;
}
//i 从最左边的元素开始找 大于基准点的元素
while (i < j && array[i] <= pv) { //array[i] <= pv -- i开始位于左边界,且 pv 为左边界的元素 如果不相等,就无法进入循环
i++;
}
swap(array, i, j); // j 找到小于基准点的元素 i找到大于基准点的元素,两者位置发生互换
}
swap(array, low, j); //基准点 和 i(i和j相等) 互换,i 为 新的分区位置
System.out.println(Arrays.toString(array) + "j=" + j);
return j;
}
public static void swap(int[] array,int i,int j){//将数组中下标为i和j的元素分别交换位置
int t = array[i]; //先将下标为 i 的元素取出来放进缓存区
array[i] = array[j];//将下标为 j 的元素放到原先下标为 i 的位置
array[j] = t; //将下标为 i 的元素 从缓存区里取出来放入 原先下标为 j 的位置
}
}
[1, 3, 4, 2, 5, 8, 9, 7]j=4
[1, 3, 4, 2, 5, 8, 9, 7]j=0
[1, 2, 3, 4, 5, 8, 9, 7]j=2
[1, 2, 3, 4, 5, 7, 8, 9]j=6
6. 归并排序
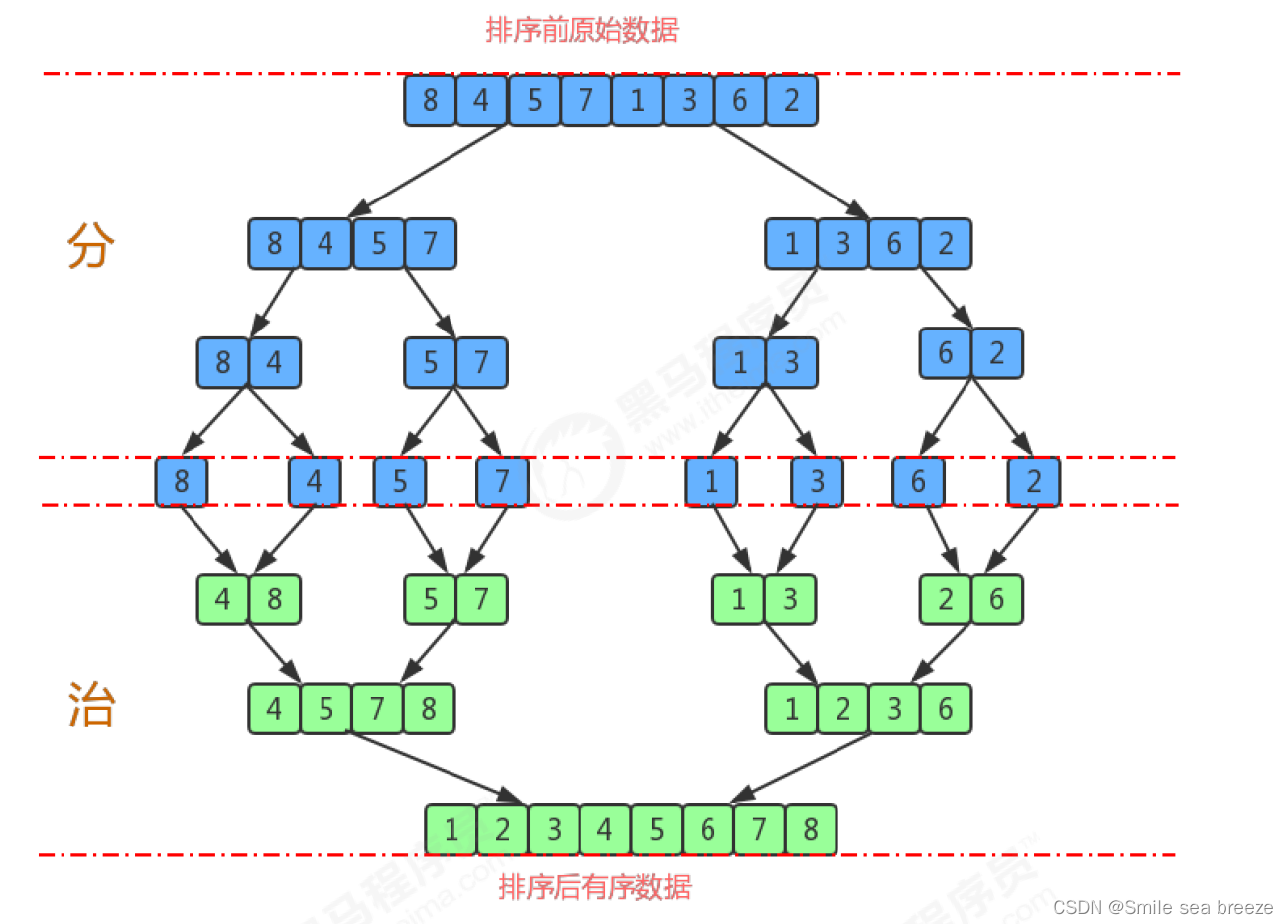
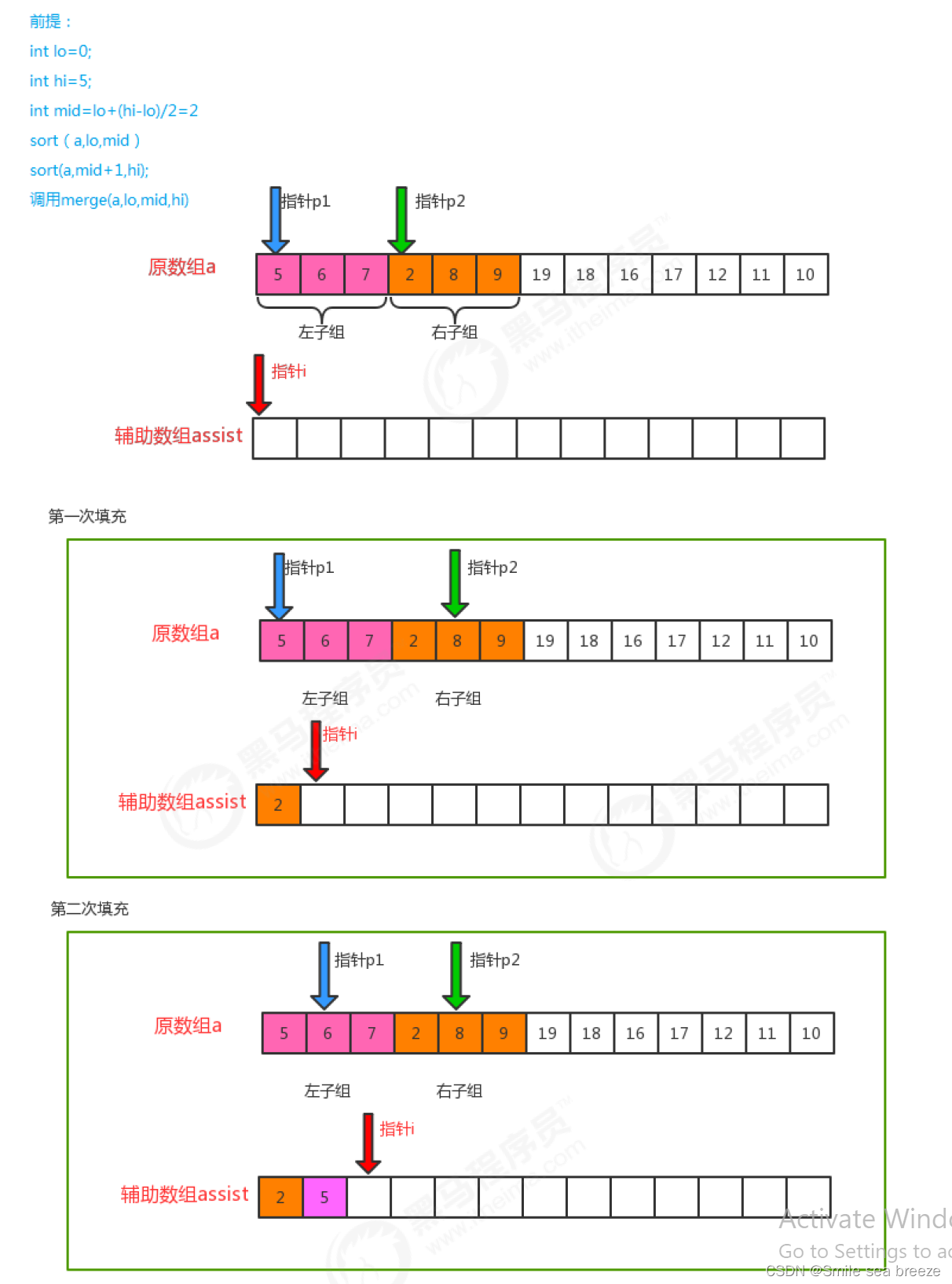
public class MergeSort {
public static void main(String[] args) {
int[] array = {9,3,7,2,5,8,1,4};
int[] answer = cut(array);
System.out.println(Arrays.toString(answer));
}
public static int[] cut(int[]data){
if(data.length == 1){//如果a的长度为1,表示数组只有一个元素,数组数据划分结束
return data;
}
else {
int leftArrLength = data.length / 2;//数组的元素个数一分为二,左边数组元素个数为元素组的一半
int rightArrLength = data.length - leftArrLength;//右边数组元素个数为元素组个数-左边数组元素个数
int [] left = new int[leftArrLength]; //被划分元素组左边,创建新数组为left
int [] right = new int[rightArrLength];//被划分元素组右边,创建新数组为right
for(int i = 0; i < leftArrLength; i++){//遍历数组元素放入left中
left[i] = data[i];
}
for(int i=leftArrLength; i<data.length; i++){//遍历数组元素放入right中
right[i-leftArrLength] = data[i];
}
System.out.println(Arrays.toString(left));
System.out.println(Arrays.toString(right));
return merge(cut(left), cut(right));//递归a数组中的元素,直到数组元素为1,之后进数组合并
}
}
public static int[] merge(int[] leftArr, int[] rightArr) {//数组合并
int finalArrsize = leftArr.length + rightArr.length;//新数组长度为左右两边数组合并的长度
int[] finalArr = new int[finalArrsize];//创建新的数组,为合并后的数组
int leftArrCounter = 0;//指针从0开始
int rightArrCounter = 0;//指针从0开始
int finalArrCounter = 0;//指针从0开始
while (finalArrCounter < finalArrsize) {
if (leftArrCounter >= leftArr.length) {
finalArr[finalArrCounter] = rightArr[rightArrCounter];
rightArrCounter++;
} else if (rightArrCounter >= rightArr.length) {
finalArr[finalArrCounter] = leftArr[leftArrCounter];
leftArrCounter++;
} else if (leftArr[leftArrCounter] < rightArr[rightArrCounter]) {
finalArr[finalArrCounter] = leftArr[leftArrCounter];
leftArrCounter++;
} else {
finalArr[finalArrCounter] = rightArr[rightArrCounter];
rightArrCounter++;
}
finalArrCounter++;
}
return finalArr;
}
}
[9, 3, 7, 2]
[5, 8, 1, 4]
[9, 3]
[7, 2]
[9]
[3]
[7]
[2]
[5, 8]
[1, 4]
[5]
[8]
[1]
[4]
[1, 2, 3, 4, 5, 7, 8, 9]


![[附源码]计算机毕业设计绿色生活交流社区网站Springboot程序](https://img-blog.csdnimg.cn/0fb4171aa08946cf99bfb84dde599aa2.png)

![[附源码]Python计算机毕业设计Django物业管理系统](https://img-blog.csdnimg.cn/b6ee11bd17c24510aca5f05c84db5b69.png)