文章目录

常见逻辑门以及含义

一、Hadamard（H）门

二、Pauli-X 门

三、Pauli-Y 门

四、Pauli-Z 门

五、旋转门（rotation operators）

1、RX（θ）门

2、RY（θ）门

3、RZ（θ）门

六、多量子比特逻辑门

七、CNOT 门

八、CR 门

九、iSWAP 门

---

常见逻辑门以及含义

一、Hadamard（H）门

Hadamard门是一种可将基态变为叠加态的量子逻辑门，有时简称为H门。Hadamard门作用在单比特上，它将基态|0〉变成，将基态|1〉变成。

Hadamard门矩阵形式为

其在线路上显示如下图所示：

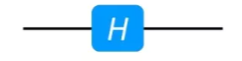
假设，H门作用在任意量子态|ψ〉= α|0〉+ β|1〉上面，得到新的量子态为：

二、Pauli-X 门

Pauli-X门作用在单量子比特上，它是经典计算机NOT门的量子等价，将量子态进行翻转，量子态变化方式为：

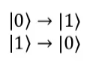
Pauli-X门矩阵形式为泡利矩阵，即：

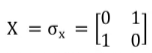
Pauli-X门矩阵又称NOT门；其在线路上显示如下图所示：

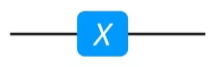
假设，NOT门作用在任意量子态|ψ〉= α|0〉+ β|1〉上面，得到新的量子态为：

三、Pauli-Y 门

Pauli-Y门作用在单量子比特上，作用效果为绕Bloch球Y轴旋转角度π，Pauli-Y门的矩阵形式为泡利矩阵，即：

其在线路上显示如下图所示：

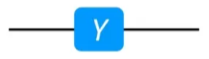
假设，Pauli-Y门作用在任意量子态|ψ〉= α|0〉+ β|1〉上面，得到新的量子态为：

四、Pauli-Z 门

Pauli-Z门作用在单量子比特上，作用效果是绕Bloch球Z轴旋转角度，Pauli-Z门矩阵形式为泡利矩阵，即：

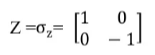
其在线路上显示如下图所示：

假设，Pauli-Z门作用在任意量子态|ψ〉= α|0〉+ β|1〉上面，得到新的量子态为：

五、旋转门（rotation operators）

分别用不同的泡利矩阵作为生成元是构成RX，RY，RZ的方法。

1、RX（θ）门

RX门由Pauli-X矩阵作为生成元生成，其矩阵形式为

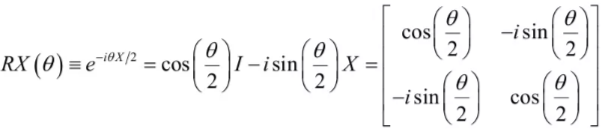
其在线路上显示如下图所示：

假设，RX（π/2）门作用在任意量子态|ψ〉= α|0〉+ β|1〉上面，得到新的量子态为：

2、RY（θ）门

RY门由Pauli-Y矩阵作为生成元生成，其矩阵形式为

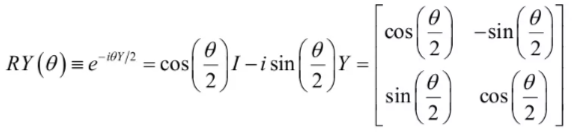
其在线路上显示如下图所示：

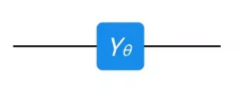
假设，RY（π/2）门作用在任意量子态|ψ〉= α|0〉+ β|1〉上面，得到新的量子态为：

3、RZ（θ）门

RZ又称相位转化门（phase-shift gate），其由Z门为生成元生成，矩阵形式为

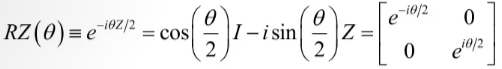
上式还可以写为

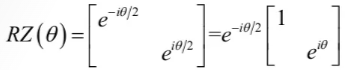
由于矩阵

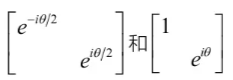
只差一个整体相位（global phases），只考虑单门的话，两个矩阵做成的量子逻辑门是等价的，即有时RZ门的矩阵形式写作

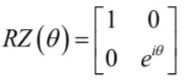
RZ量子逻辑门作用在基态上的效果为

由于全局相位没有物理意义，并没有对计算基|0〉和|1〉做任何的改变，而是在原来的态上绕Z轴逆时针旋转角。

其在线路上显示如下图所示：

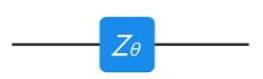
假设，RZ（π/2）门作用在任意量子态|ψ〉= α|0〉+ β|1〉上面，得到新的量子态为：

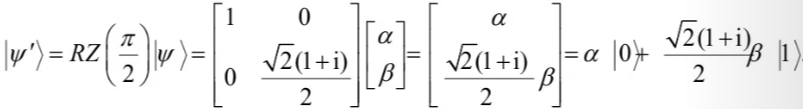
RX，RY，RZ意味着将量子态在布洛赫球上分别绕着X，Y，Z轴旋转θ角度，所以RX，RY能带来概率幅的变化，而RZ只有相位的变化。那么，共同使用这三种操作能使量子态在整个布洛赫球上自由移动。

六、多量子比特逻辑门

不论是在经典计算还是量子计算中，两量子比特门无疑是建立量子比特之间联系的最重要桥梁。不同于经典计算中的与或非门及它们的组合，量子逻辑门要求所有的逻辑操作必须是酉变换，所以输入和输出的比特数量是相等的。

在描述两量子比特门之前，必须要将之前对于单量子比特的表示方式扩展一下。联立两个量子比特或者两个以上的量子比特时，就用到复合系统中量子态演化的假设。

对于一个n量子比特，n量子比特系统的计算基就有单位正交失量组成，借助于经典比特的进位方式对量子比特进行标记，从左到右依次是二进制中的从高位到低位，也就是说中为高位，为低位。

比如对于一个2量子比特的系统，其计算基分别记做

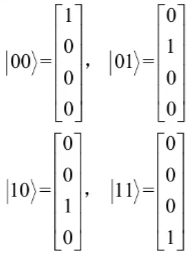
在基态|1〉中，左侧的0对应的位为高位，1对应的位为低位。

在介绍2比特量子逻辑门时，会使用如下图的图标：

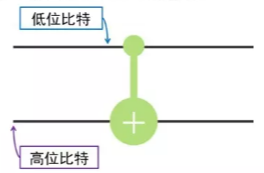
每根线表示一个量子比特演化的路线，这和单比特门中的横线是类似的，不一样的是这两根线有位次之分，从上到下依次分别表示从低位到高位的量子比特演化的路线。这个图标横跨两个量子比特，它代表将一个两比特门作用在这两个量子比特上，这个图标代表的是CNOT门。

七、CNOT 门

控制非门（Control-NOT），通常用CNOT进行表示，是一种普遍使用的两量子比特门。

若低位为控制比特，那么它具有如下的矩阵形式：

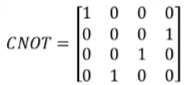
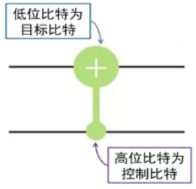
对应的CNOT门在线路中显示如下图：

含实点的路线对应的量子比特称为控制比特（control qubit），含+号的路线对应的量子比特为目标比特（target qubit）。

假设，CNOT门作用分别作用在基态|ψ〉= |00〉、|01〉、|10〉、|11〉上面，得到新的量子态为：

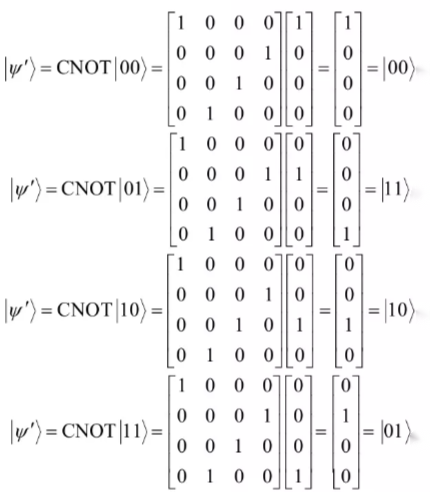
由于低位比特为控制比特，高位比特为目标比特，所以当低位比特位置对应为1时，高位比特就会被取反；当低位比特位置为0时，不对高位比特做任何操作。

若高位比特为控制比特，那么它具有如下的矩阵形式：

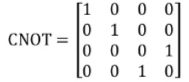
CNOT门在线路中显示如下图：

假设，高位为控制比特，CNOT门分别作用在基态|ψ〉= |00〉、|01〉、|10〉、|11〉上，那么，可以计算四个两量子比特的计算基经CNOT门的演化结果如下图所示：

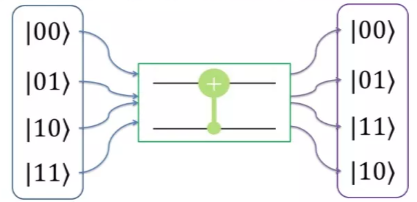
从上例可以看出CNOT门的含义是当控制比特为|0〉态时，目标比特不发生改变；当控制比特为|1〉态时，对目标比特执行X门（量子非门）操作。要注意的是控制比特和目标比特的地位是不能交换的。

八、CR 门

控制相位门（Controlled phase gate）和控制非门类似，通常记为CR（CPhase），其矩阵形式如下

CPhase门在线路中显示如下图：

 

在CPhase门的图标中，含实点的路线对应的量子比特称为控制比特（control gubit），含CR字母的路线对应的量子比特为目标比特（target qubit）。

当控制比特为|0〉态时，目标比特不发生改变；当控制比特为|1〉态时，对目标比特执行相转变门（phase-shift gate），其特殊的是，控制相位门里交换控制比特和目标比特的角色，矩阵形式不会发生任何改变。

九、iSWAP 门

iSWAP门的主要作用是交换两个比特的状态，并且赋予其π/2相位；经典电路中也有SWAP门，但是iSWAP是量子计算中特有的。iSWAP门在某些体系中是较容易实现的两比特逻辑门，它是由​​​​​​​作为生成元生成，需要将矩阵对角化，iSWAP的矩阵表示如下：

iSWAP门在线路中显示如下图：

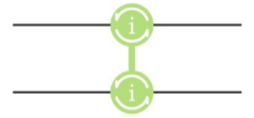
通常会用一个完整的翻转，即θ=π/2的情况来指代iSWAP。当角度为iSWAP的一半时，即θ=π/4，称之为√iSWAP。对于iSWAP门而言，两个比特之间地位是对等的，不存在控制和受控的关系。

---

• 📢博客主页：https://lansonli.blog.csdn.net
• 📢欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正！
• 📢本文由 Lansonli 原创，首发于 CSDN博客🙉
• 📢停下休息的时候不要忘了别人还在奔跑，希望大家抓紧时间学习，全力奔赴更美好的生活✨