半局积分算法的局限性是要求采样的波形为正弦波。当被采样的模拟量不是正弦波而是一个周期性时间函数时，可采用傅氏变换算法。傅氏变换算法来自于傅里叶级数，即一个周期性函数I（t）可用傅里叶级数展开为各次谐波的正弦项和余弦项之和，可用下式表示

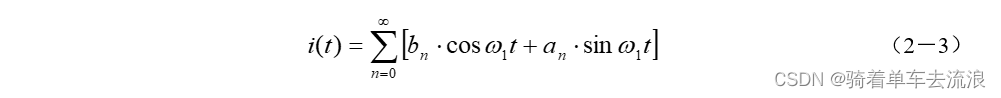
式中n为自然数，n=0，1，2…表示谐波分量次数。于是电流i（t）中的基波分量可表示为

 i（t）还可以表示为一般表达式

 

式中I1为基波有效值，为t=0时基波分量初相角。

将sin（wt＋a）用和角公式展开，再与式（2－4）比较，可以得到和同和的关系。

 从式（2－6）和式（2－7）可以看出只要求出基波的正弦和余弦项幅值，就很容易求得基波的有效值和初相位角。

    根据傅氏级数的逆变换原理可求得和。

 

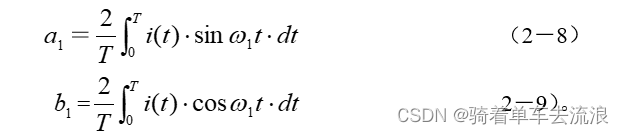
   在用微机计算和时，通常都是采用有限离散方法算得，即将在（t）用各采样点数值代入，通过梯形法求和来代替积分法。考虑到N·， 时式（2－8）和式（2－9）可表示为

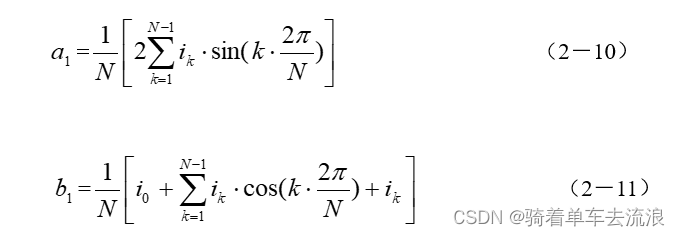
式中N为一周采样点数，为第k次采样值，，分别为k=0和N时的采样值。当N=12时采样间隔Ts一般用角度表示为30。

    算出和后，根据式（2－6）、式（2－7）不难得到基波的有效值和相角                                                    af＋ bf

 

与半周积分算法比较，傅氏变换算法可以计算周期性时间函数，还可算出初相位角，其积分运算结果同样具有数字滤波功能，运算工作量也不大。但这种算法用于暂态采样计算时受输入模拟量中的非周期分量影响较大，理论分析在最不利的条件下可产生15％以上的误差，通常还需要采用一些补偿措施加以克服。目前许多较先进的保护装置都采用了傅氏变换算法，例如LFP—900系列保护装置。