题目描述

链接：添加链接描述

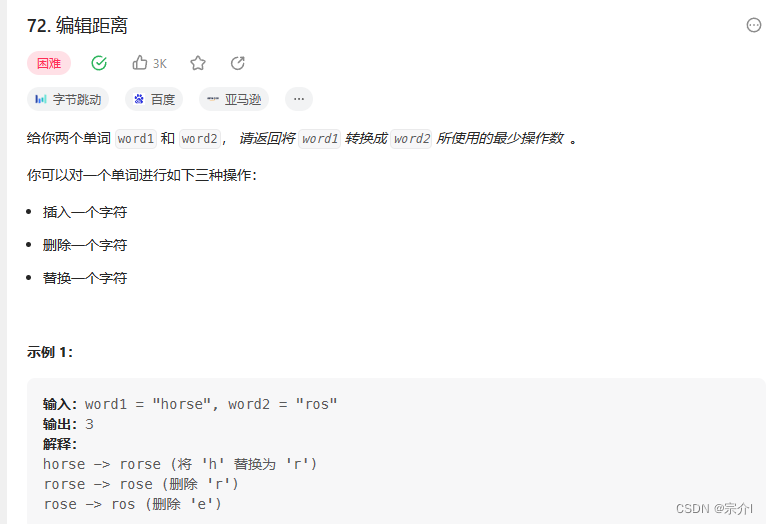
跟只考虑删除的完全一样，只不过是dp[i-1][j-1]+1

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        # dp[i][j]：以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，想要达到相等，所需要最小编辑距离。
        dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)]
        for i in range(len(word1)+1):
            dp[i][0] = i
        for j in range(len(word2)+1):
            dp[0][j] = j
        for i in range(1, len(word1)+1):
            for j in range(1, len(word2)+1):
                if word1[i-1] == word2[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = min(dp[i-1][j-1]+1, dp[i-1][j] + 1, dp[i][j-1] + 1)
                    # 当word1[i - 1] 与 word2[j - 1]不相同的时候，进行改增删：
                    # 情况一：替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同
                    # 情况二：word1删除一个元素，即下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。
                    # 情况三：word2删除一个元素，即下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。
        return dp[-1][-1]
        
# 替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同，此时不用增删加元素。
# 可以回顾一下，if (word1[i - 1] == word2[j - 1])的时候我们的操作 
# 是 dp[i][j] = dp[i - 1][j - 1] 对吧。
# 那么只需要一次替换的操作，就可以让 word1[i - 1] 和 word2[j - 1] 相同。
# 所以 dp[i][j] = dp[i - 1][j - 1] + 1;

# 这里有同学发现了，怎么都是删除元素，添加元素去哪了。
# word2添加一个元素，相当于word1删除一个元素
# 例如 word1 = "ad" ，word2 = "a"
# word1删除元素'd' 和 word2添加一个元素'd'，变成word1="a", word2="ad"， 
# 最终的操作数是一样！

备注

在这里插入代码片