1 介绍

TeX（计算机排版系统）

七十年代末，Donald E. Knuth在看自己的《电脑编程的艺术》校样时，感觉计算机排版的校样质量低到无法忍受，于是决定自己开发一个高质量的计算机排版系统，这样就有了 TeX 。
TeX 在希腊语中这个词的意思是“科技”和“艺术”。
‎TeX 是一个排版系统。它提供了许多命令，需要你自己指定文档格式，比如字号，行距，页面分割等等。听起来就很麻烦，所以这需要专业排版的人员来搞。一般用户不可能为了排版而学习他整套系统。

LaTeX（TeX宏集）

LaTeX 是一套建在 TeX 之上的高质量的排版格式，可以生成复杂的表格与数学公式，是当前电子与数学出版行业的事实标准。
LaTeX 是当今世界上最流行和使用最广泛的TEX宏集。
由美国计算机科学家莱斯利·兰伯特在20世纪80年代初期开发，利用这种格式系统的处理，即使用户没有排版和程序设计的知识也可以充分发挥由TeX所提供的强大功能。

‎LaTeX 是一套建在 TeX 之上的宏。LaTeX 背后的理念是将焦点从‎‎格式‎‎转移到文档‎‎内容‎‎。在 LaTeX 命令是为了给文档内容提供结构。已经按照一套排版标准编写好模板，你只需要指定就行了。

KaTeX 和 MathJax

俩都是JavaScript渲染器。将 LaTeX 表达的内容显示出来。
目前来说，在网页上显示数学公式最常用的方案是引入 JavaScript 对 LaTeX 代码渲染，如维基百科、segmentfault 都是采用这样的方案，其中使用最多的库是 MathJax 和 KaTeX。

2 注意点

单双美元符号包裹问题

csdn 中 LaTex 语法使用，Markdown中两种输入公式的方法：一是行内公式（inline），用一对美元符号“$”包裹。二是整行公式（displayed）【占据整行】，用一对紧挨的两个美元符号“$$ ”包裹。

注：

1. 有时单美元符号，显示不对时，可以使用双美元符号。
2. 防止排版乱，可以使用双美元符号。

语法	输出
$\sigma$	$\sigma$
$\sqrt[3]{\frac{x^3+y^3}{2}}*$	$\sqrt[3]{\frac{x^3+y^3}{2}}\ast$
$$\dfrac{2}{4} = 0.5 \qquad \dfrac{2}{c + \dfrac{2}{d + \dfrac{2}{4}}} = a$$	$$\frac{2}{4}=0.5\frac{2}{c+\frac{2}{d+\frac{2}{4}}}=a$$

$$
x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}
$$

$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

$x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

KaTeX 有些不支持

CSDN 中的 Markdown 使用的是 KaTeX，KaTex 有些不支持。
详见：https://katex.org/docs/support_table.html
举例：‘\̲i̲i̲i̲i̲n̲t̲’

KaTeX parse error: Expected 'EOF', got '\iiiint' at position 1

3 语法

保留字符

LaTeX 环境中具有特殊含义的保留字符，不能直接使用，必须通过指定的语法实现：

序号	符号	LaTeX	序号	符号	LaTeX
1	#	\#	6	{	\{
2	%	\%	7	}	\}
3	∧	^\wedge	8	∼	\sim
4	&	\&	9	∖	\backslash
5	_	\_

希腊字母

序号	标准符号	LaTeX	首字母大写	LaTeX	使用 var 前缀	LaTeX	读音
1	α	\alpha					/ˈælfə/
2	β	\beta					/ˈbeɪtə/
3	γ	\gamma	Γ	\Gamma	Γ	\varGamma	/ˈɡæmə/
4	δ	\delta	Δ	\Delta	Δ	\varDelta	/ˈdɛltə/
5	ϵ	\epsilon			ε	\varepsilon	/ˈɛpsɪlɒn/
6	ζ	\zeta					/ˈzeɪtə/
7	η	\eta					/ˈeɪtə/
8	θ	\theta	Θ	\Theta	ϑ、Θ	\vartheta、\varTheta	/ˈθiːtə/
9	ι	\iota					/aɪˈoʊtə/
10	κ	\kappa			ϰ	\varkappa	/ˈkæpə/
11	λ	\lambda	Λ	\Lambda	Λ	\varLambda	/ˈlæmdə/
12	μ	\mu					/mjuː/
13	ν	\nu					/njuː/
14	ξ	\xi	Ξ	\Xi	Ξ	\varXi	/zaɪ, ksaɪ/
15	o	o	O	O			/ˈɒmɪkrɒn/
16	π	\pi	Π	\Pi	ϖ、Π	\varpi、\varPi	/paɪ/
17	ρ	\rho			ϱ	\varrho	/roʊ/
18	σ	\sigma	Σ	\Sigma	ς、Σ	\varsigma、\varSigma	/ˈsɪɡmə/
19	τ	\tau					/taʊ, tɔː/
20	υ	\upsilon	Υ	\Upsilon	Υ	\varUpsilon	/ˈʌpsɪlɒn/
21	ϕ	\phi	Φ	\Phi	φ、Φ	\varphi、\varPhi	/faɪ/
22	χ	\chi					/kaɪ/
23	ψ	\psi	Ψ	\Psi	Ψ	\varPsi	/psaɪ/
24	ω	\omega	Ω	\Omega	Ω	\varOmega	/oʊˈmeɪɡə/
25	ϝ	\digamma					/daɪ’gæmə/

希伯来字母

序号	符号	LaTeX	英文	序号	符号	LaTeX	英文
1	ℵ	\aleph	aleph	3	ℷ	\gimel	gimel
2	ℶ	\beth	beth	4	ℸ	\daleth	daleth

二元运算符

序号	符号	LaTeX	序号	符号	LaTeX
1	+	+	20	∙	\bullet
2	−	-	21	⊕	\oplus
3	×	\times	22	⊖	\ominus
4	÷	\div	23	⊙	\odot
5	±	\pm	24	⊘	\oslash
6	∓	\mp	25	⊗	\otimes
7	◃	\triangleleft	26	◯	\bigcirc
8	▹	\triangleright	27	⋄	\diamond
9	⋅	\cdot	28	⊎	\uplus
10	∖	\setminus	29	△	\bigtriangleup
11	⋆	\star	30	▽	\bigtriangledown
12	∗	\ast	31	⊲	\lhd
13	∪	\cup	32	⊳	\rhd
14	∩	\cap	33	⊴	\unlhd
15	⊔	\sqcup	34	⊵	\unrhd
16	⊓	\sqcap	35	⨿	\amalg
17	∨	\vee	36	≀	\wr
18	∧	\wedge	37	†	\dagger
19	∘	\circ	38	‡	\ddagger

二元关系符

序号	符号	LaTeX	序号	符号	LaTeX
1	=	=	49	$⪈$	\gneq
2	≠	\ne	50	≧	\geqq
3	≠	\neq	51	$\ngeqq$	\ngeq
4	≡	\equiv	52	$$	\ngeqq
5	$\not\equiv$	\not\equiv	53	≩	\gneqq
6	≐	\doteq	54	≩	\gvertneqq
7	≑	\doteqdot	55	≶	\lessgtr
8	$\stackrel{\underset{\mathrm{def}}{}}{=}$	\overset{\underset{\mathrm{def}}{}}{=}	56	⋚	\lesseqgtr
9	:=	:=	57	⪋	\lesseqqgtr
10	∼	\sim	58	≷	\gtrless
11	≁	\nsim	59	⋛	\gtreqless
12	∽	\backsim	60	⪌	\gtreqqless
13	∼	\thicksim	61	⩽	\leqslant
14	≃	\simeq	62	⪇	\nleqslant
15	⋍	\backsimeq	63	⪕	\eqslantless
16	≂	\eqsim	64	⩾	\geqslant
17	≅	\cong	65	$$	\ngeqslant
18	≇	\ncong	66	⪖	\eqslantgtr
19	≈	\approx	67	≲	\lesssim
20	≈	\thickapprox	68	⋦	\lnsim
21	≊	\approxeq	69	⪅	\lessapprox
22	≍	\asymp	70	⪉	\lnapprox
23	∝	\propto	71	≳	\gtrsim
24	∝	\varpropto	72	⋧	\gnsim
25	<	<	73	⪆	\gtrapprox
26	$\nless$	\nless	74	⪊	\gnapprox
27	≪	\ll	75	≺	\prec
28	≪̸	\not\ll	76	⊀	\nprec
29	⋘	\lll	77	⪯	\preceq
30	⋘̸	\not\lll	78	⋠	\npreceq
31	⋖	\lessdot	79	⪵	\precneqq
32	>	>	80	≻	\succ
33	$\ngtr$	\ngtr	81	⊁	\nsucc
34	≫	\gg	82	⪰	\succeq
35	$/\gg$	\not\gg	83	⋡	\nsucceq
36	⋙	\ggg	84	⪶	\succneqq
37	$/⋙$	\not\ggg	85	≼	\preccurlyeq
38	⋗	\gtrdot	86	⋞	\curlyeqprec
39	≤	\le	87	≽	\succcurlyeq
40	≤	\leq	88	⋟	\curlyeqsucc
41	⪇	\lneq	89	≾	\precsim
42	≦	\leqq	90	⋨	\precnsim
43	$\nleqq$	\nleq	91	⪷	\precapprox
44	$$	\nleqq	92	⪹	\precnapprox
45	≨	\lneqq	93	≿	\succsim
46	≨	\lvertneqq	94	⋩	\succnsim
47	≥	\ge	95	⪸	\succapprox
48	≥	\geq	96	⪺	\succnapprox

几何符号

序号	符号	LaTeX	序号	符号	LaTeX
1	∥	\parallel	14	◊	\lozenge
2	∦	\nparallel	15	⧫	\blacklozenge
3	∥	\shortparallel	16	★	\bigstar
4	∦	\nshortparallel	17	◯	\bigcirc
5	⊥	\perp	18	△	\triangle
6	∠	\angle	19	△	\bigtriangleup
7	∢	\sphericalangle	20	▽	\bigtriangledown
8	∡	\measuredangle	21	△	\vartriangle
9	45∘	45^\circ	22	▽	\triangledown
10	◻	\Box	23	▴	\blacktriangle
11	◼	\blacksquare	24	▾	\blacktriangledown
12	⋄	\diamond	25	◂	\blacktriangleleft
13	◊◊	\Diamond \lozenge	26	▸	\blacktriangleright

逻辑符号

序号	符号	LaTeX	序号	符号	LaTeX
1	∀	\forall	20	¬	\neg
2	∃	\exists	21	$/R$	\not\operatorname{R}
3	∄	\nexists	22	⊥	\bot
4	∴	\therefore	23	⊤	\top
5	∵	\because	24	⊢	\vdash
6	&	\And	25	⊣	\dashv
7	∨	\lor	26	⊨	\vDash
8	∨	\vee	27	⊩	\Vdash
9	⋎	\curlyvee	28	⊨	\models
10	⋁	\bigvee	29	⊪	\Vvdash
11	∧	\land	30	⊬	\nvdash
12	∧	\wedge	31	$$⊮$$	\nVdash
13	⋏	\curlywedge	32	⊭	\nvDash
14	⋀	\bigwedge	33	$$⊯$$	\nVDash
15	$\bar{q}$	\bar{q}	34	⌜	\ulcorner
16	$\overline{abc}$	\bar{abc}	35	⌝	\urcorner
17	$\overline{q}$	\overline{q}	36	⌞	\llcorner
18	$\overline{abc}$	\overline{abc}	37	⌟	\lrcorner
19	¬	\lnot

集合符号

序号	符号	LaTeX	序号	符号	LaTeX
1	{}	\{ \}	23	⊏	\sqsubset
2	∅	\emptyset	24	⊃	\supset
3	∅	\varnothing	25	⋑	\Supset
4	∈	\in	26	⊐	\sqsupset
5	∉	\notin	27	⊆	\subseteq
6	∋	\ni	28	⊈	\nsubseteq
7	∩	\cap	29	⊊	\subsetneq
8	⋒	\Cap	30	⊊	\varsubsetneq
9	⊓	\sqcap	31	⊑	\sqsubseteq
10	⋂	\bigcap	32	⊇	\supseteq
11	∪	\cup	33	⊉	\nsupseteq
12	⋓	\Cup	34	⊋	\supsetneq
13	⊔	\sqcup	35	⊋	\varsupsetneq
14	⋃	\bigcup	36	⊒	\sqsupseteq
15	⨆	\bigsqcup	37	⫅	\subseteqq
16	⊎	\uplus	38	$$	\nsubseteqq
17	⨄	\biguplus	39	⫋	\subsetneqq
18	∖	\setminus	40	⫋	\varsubsetneqq
19	∖	\smallsetminus	41	⫆	\supseteqq
20	×	\times	42	⊉	\nsupseteqq
21	⊂	\subset	43	⫌	\supsetneqq
22	⋐	\Subset	44	⫌	\varsupsetneqq

箭头符号

序号	符号	LaTeX	序号	符号	LaTeX
1	⇛	\Rrightarrow	36	⟼	\longmapsto
2	⇚	\Lleftarrow	37	⇀	\rightharpoonup
3	⇒	\Rightarrow	38	⇁	\rightharpoondown
4	⇏	\nRightarrow	39	↼	\leftharpoonup
5	⟹	\Longrightarrow	40	↽	\leftharpoondown
6	⟹	\implies	41	↿	\upharpoonleft
7	⇐	\Leftarrow	42	↾	\upharpoonright
8	⇍	\nLeftarrow	43	⇃	\downharpoonleft
9	⟸	\Longleftarrow	44	⇂	\downharpoonright
10	⇔	\Leftrightarrow	45	⇌	\rightleftharpoons
11	⇎	\nLeftrightarrow	46	⇋	\leftrightharpoons
12	⟺	\Longleftrightarrow	47	↶	\curvearrowleft
13	⟺	\iff	48	↺	\circlearrowleft
14	⇑	\Uparrow	49	↰	\Lsh
15	⇓	\Downarrow	50	⇈	\upuparrows
16	⇕	\Updownarrow	51	⇉	\rightrightarrows
17	→	\rightarrow	52	⇄	\rightleftarrows
18	→	\to	53	↣	\rightarrowtail
19	$\nrightarrow$	\nrightarrow	54	↬	\looparrowright
20	⟶	\longrightarrow	55	↷	\curvearrowright
21	←	\leftarrow	56	↻	\circlearrowright
22	←	\gets	57	↱	\Rsh
23	$\nleftarrow$	\nleftarrow	58	⇊	\downdownarrows
24	⟵	\longleftarrow	59	⇇	\leftleftarrows
25	↔	\leftrightarrow	60	⇆	\leftrightarrows
26	$\nleftrightarrow$	\nleftrightarrow	61	↢	\leftarrowtail
27	⟷	\longleftrightarrow	62	↫	\looparrowleft
28	↑	\uparrow	63	↪	\hookrightarrow
29	↓	\downarrow	64	↩	\hookleftarrow
30	↕	\updownarrow	65	⊸	\multimap
31	↗	\nearrow	66	↭	\leftrightsquigarrow
32	↙	\swarrow	67	⇝	\rightsquigarrow
33	↖	\nwarrow	68	↠	\twoheadrightarrow
34	↘	\searrow	69	↞	\twoheadleftarrow
35	↦	\mapsto

特殊符号

序号	符号	LaTeX	序号	符号	LaTeX
1	∞	\infty	33	♭	\flat
2	ℵ	\aleph	34	♮	\natural
3	∁	\complement	35	♯	\sharp
4	∍	\backepsilon	36	╱	\diagup
5	ð	\eth	37	╲	\diagdown
6	Ⅎ	\Finv	38	⋅	\centerdot
7	ℏ	\hbar	39	⋉	\ltimes
8	ℑ	\Im	40	⋊	\rtimes
9	ı	\imath	41	⋋	\leftthreetimes
10	ȷ	\jmath	42	⋌	\rightthreetimes
11	𝕜	\Bbbk	43	≖	\eqcirc
12	ℓ	\ell	44	≗	\circeq
13	℧	\mho	45	≜	\triangleq
14	℘	\wp	46	≏	\bumpeq
15	ℜ	\Re	47	≎	\Bumpeq
16	Ⓢ	\circledS	48	≑	\doteqdot
17	⨿	\amalg	49	≓	\risingdotseq
18	%	\%	50	≒	\fallingdotseq
19	†	\dagger	51	⊺	\intercal
20	‡	\ddagger	52	⊼	\barwedge
21	…	\ldots	53	⊻	\veebar
22	⋯	\cdots	54	⩞	\doublebarwedge
23	⌣	\smile	55	≬	\between
24	⌢	\frown	56	⋔	\pitchfork
25	≀	\wr	57	⊲	\vartriangleleft
26	◃	\triangleleft	58	⋪	\ntriangleleft
27	▹	\triangleright	59	⊳	\vartriangleright
28	♢	\diamondsuit	60	⋫	\ntriangleright
29	♡	\heartsuit	61	⊴	\trianglelefteq
30	♣	\clubsuit	62	⋬	\ntrianglelefteq
31	♠	\spadesuit	63	⊵	\trianglerighteq
32	⅁	\Game	64	⋭	\ntrianglerighteq

分数

类型	符号	LaTeX
分数	$\frac{2}{4}x=0.5xor\frac{2}{4}x=0.5x$	\frac{2}{4}x=0.5x or {2 \over 4}x=0.5x
小型分数	24x=0.5x	\tfrac{2}{4}x = 0.5x
大型分数 （不嵌套）	$$\frac{2}{4}=0.5\frac{2}{c+\frac{2}{d+\frac{2}{4}}}=a$$	\dfrac{2}{4} = 0.5 \qquad \dfrac{2}{c + \dfrac{2}{d + \dfrac{2}{4}}} = a
大型分数 （嵌套）	$\frac{2}{c+\frac{2}{d+\frac{2}{4}}}=a$	\cfrac{2}{c + \cfrac{2}{d + \cfrac{2}{4}}} = a

数值函数

符号	LaTeX
${\exp }_{a}b=a^b,\exp b=e^b,10^m$	\exp_a b = a^b, \exp b = e^b, 10^m
$\ln c,\lg d=\log e,{\log }_{10}f$	\ln c, \lg d = \log e, \log_{10} f
$\sin a,\cos b,\tan c,\cot d,\sec e,\csc f$	\sin a, \cos b, \tan c, \cot d, \sec e, \csc f
$\arcsin a,\arccos b,\arctan c$	\arcsin a, \arccos b, \arctan c
$\mathrm{arccot}d,\mathrm{arcsec}e,\mathrm{arccsc}f$	\operatorname{arccot} d, \operatorname{arcsec} e, \operatorname{arccsc} f
$\sinh a,\cosh b,\tanh c,\coth d$	\sinh a, \cosh b, \tanh c, \coth d
$\mathrm{sh}k,\mathrm{ch}l,\mathrm{th}m,\coth n$	\operatorname{sh}k, \operatorname{ch}l, \operatorname{th}m, \operatorname{coth}n
$\mathrm{argsh}o,\mathrm{argch}p,\mathrm{argth}q$	\operatorname{argsh}o, \operatorname{argch}p, \operatorname{argth}q
$\mathrm{sgn}r,\left|s\right|$	\operatorname{sgn}r, \left\vert s \right\vert
min(x,y),max(x,y)	\min(x,y), \max(x,y)

如果需要使用特殊的函数符号，那么可以采用 \operatorname{} 命令进行自定义：

符号	LaTeX
$\mathrm{mydefine}x$	\operatorname{mydefine}x

根式

符号	LaTeX	符号	LaTeX
√	\surd	$\sqrt[n]{\pi }$	\sqrt[n]{\pi}
π	\sqrt{\pi}	$\sqrt[3]{\frac{x^3+y^3}{2}}$	\sqrt[3]{\frac{x^3+y^3}{2}}

微分与导数

符号	LaTeX
dt,dt,∂t,∇ψ	dt, \mathrm{d}t, \partial t, \nabla\psi
$dy/dx,\mathrm{d}y/\mathrm{d}x,\frac{dy}{dx},\frac{\mathrm{d}y}{\mathrm{d}x},\frac{{\partial }^2}{\partial x_1\partial x_2}y$	dy/dx, \mathrm{d}y/\mathrm{d}x, \frac{dy}{dx}, \frac{\mathrm{d}y}{\mathrm{d}x}, \frac{\partial^2}{\partial x_1\partial x_2}y
$\prime ,‵,f^{\prime },f^{\prime },f^{\prime \prime },f^{(3)},\dot{y},\ddot{y}$	\prime, \backprime, f^\prime, f', f'', f^{(3)}, \dot y, \ddot y

模运算

符号	LaTeX
$s_k\equiv 0(\mathrm{mod}m)$	s_k \equiv 0 \pmod{m}
$a\mathrm{mod}b$	a \bmod b
$\gcd (m,n),\mathrm{lcm}(m,n)$	\gcd(m, n), \operatorname{lcm}(m, n)
$\mid ,\nmid ,\mid ,$	\mid, \nmid, \shortmid, \nshortmid

极限

符号	LaTeX
${\lim }_{n\to \infty }{x}_n$	\lim_{n \to \infty}x_n
${\lim }_{n\to \infty }{x}_n$	\textstyle \lim_{n \to \infty}x_n

范围与预测

符号	LaTeX
$\min x,\max y,\inf s,\sup t$	\min x, \max y, \inf s, \sup t
$\lim u,\mathrm{liminf}v,\mathrm{limsup}w$	\lim u, \liminf v, \limsup w
$\dim p,\mathrm{deg}q,\det m,\ker \varphi$	\dim p, \deg q, \det m, \ker\phi
$\mathrm{Pr}j,\mathrm{hom}l,\Vert z\Vert ,\arg z$	\Pr j, \hom l, \lVert z \rVert, \arg z

积分

符号	LaTeX
$\underset{1}{\overset{3}{\int }}\frac{e^3/x}{x^2}dx$	\int\limits_{1}^{3}\frac{e^3/x}{x^2}\, dx
${\int }_1^3\frac{e^3/x}{x^2}dx$	\int_{1}^{3}\frac{e^3/x}{x^2}\, dx
$\underset{-N}{\overset{N}{\int }}{e}^{x}dx$	\textstyle \int\limits_{-N}^{N} e^x dx
${\int }_{-N}^N{e}^{x}dx$	\textstyle \int_{-N}^{N} e^x dx
$\underset{D}{\iint }dxdy$	\iint\limits_D dx\,dy
$\underset{E}{\iiint }dxdydz$	\iiint\limits_E dx\,dy\,dz
$\int \underset{F}{\iiint }dxdydzdt$	\iiiint\limits_F dx\,dy\,dz\,dt
${\int }_{(x,y)\in C}{x}^{3}dx+4y^{2}dy$	\int_{(x,y)\in C} x^3\, dx + 4y^2\, dy
${\oint }_{(x,y)\in C}{x}^{3}dx+4y^{2}dy$	\oint_{(x,y)\in C} x^3\, dx + 4y^2\, dy

注意：积分符号采用 \int\_{}^{} 命令调用，双重积分符号采用 \iint\_{}^{}，以此类推，最高可以支持四重积分。不过KaTex不支持四重积分。

曲线积分可以使用 \oint 命令调用，但是 MathJax 并不支持该语法，因此在开启了 Unicode 扩展的前提下，可以改为采用 \unicode{} 命令调用：

符号	LaTeX	描述
∯∯c	\unicode{8751} \unicode{x222F}_C	曲面积分符号的 Unicode 码十进制为 8751,十六进制为 x222F；
∰∰c	\unicode{8752} \unicode{x2230}_C	三维曲面积分符号的 Unicode 码十进制为 8752,十六进制为 x2230；
∱∱c∲∳c∲∲c	\unicode{8753} \unicode{x2231}_c \unicode{8754} \unicode{x2232}_c \unicode{8755} \unicode{x2233}_c	其它积分符号；

大型运算符

分类	符号	LaTeX	符号	LaTeX
求和	${\sum }_a^b$	\sum_{a}^{b}	${\sum }_a^b$	\textstyle \sum_{a}^{b}
连乘积	${\prod }_a^b$	\prod_{a}^{b}	${\prod }_a^b$	\textstyle \prod_{a}^{b}
余积	${\coprod }_a^b$	\coprod_{a}^{b}	${\coprod }_a^b$	\textstyle \coprod_{a}^{b}
并集	${\bigcup }_a^b$	\bigcup_{a}^{b}	${\bigcup }_a^b$	\textstyle \bigcup_{a}^{b}
交集	${\bigcap }_a^b$	\bigcap_{a}^{b}	${\bigcap }_a^b$	\textstyle \bigcap_{a}^{b}
析取	${\bigvee }_a^b$	\bigvee_{a}^{b}	${\bigvee }_a^b$	\textstyle \bigvee_{a}^{b}
合取	${\bigwedge }_a^b$	\bigwedge_{a}^{b}	${\bigwedge }_a^b$	\textstyle \bigwedge_{a}^{b}

上下标

类型	符号	代码
上标	$a^2$ $a^{x+3}$	a^2 a^{x+3}
下标	$a_2$	a_2
组合	$10^{30}{a}^{2+2}$ $ai,jb{f}^{\prime }$	10^{30} a^{2+2} a{i,j} b{f'}
上下标混合	$x_2^3$ ${x_2}^3$	x_2^3 {x_2}^3
上标的上标	$10^{10^8}$	10^{10^{8}}
混合标识	KaTeX parse error: Undefined control sequence: \sideset at position 1: \̲s̲i̲d̲e̲s̲e̲t̲{1^2}{3^4}X_a^b ${}_1^2!{\Omega }_3^4$	\sideset{1^2}{3^4}X_a^b {}_1^2!\Omega_3^4
顶标底标	ωα ωα ωγα ωα	\overset{\alpha}{\omega} \underset{\alpha}{\omega} \overset{\alpha}{\underset{\gamma}{\omega}} \stackrel{\alpha}{\omega}
导数	x′,y″,f′,f″ x′,y′′	x', y'', f', f'' x^\prime, y^{\prime\prime}
导数点	x˙,x¨	\dot{x}, \ddot{x}
上下划线与向量	$\hat{a}\bar{b}\vec{c}$ $\overrightarrow{ab}\overleftarrow{cd}\widehat{def}$ $\overline{ghi}\underline{jkl}$	\hat a \ \bar b \ \vec c \overrightarrow{a b} \ \overleftarrow{c d} \ \widehat{d e f} \overline{g h i} \ \underline{j k l}
弧度	$\stackrel{⌢}{\mathrm{AB}}$	\overset{\frown} {AB}
箭头	$A\stackrel{n+\mu -1}{\leftarrow }B\underset{T}{\overset{n\pm i-1}{\to }}C$	A \xleftarrow{n+\mu-1} B \xrightarrow[T]{n\pm i-1} C
大括号	$\stackrel{5050}{\overbrace{1+2+\cdots +100}}$	\overbrace{ 1+2+\cdots+100 }^{5050}
底部大括号	$\underset{26}{\underbrace{a+b+\cdots +z}}$	\underbrace{ a+b+\cdots+z }_{26}
求和运算	${\sum }_{k=1}^N{k}^2$	\sum_{k=1}^N k^2
文本模式下的求和运算	${\sum }_{k=1}^N{k}^2$	\textstyle \sum_{k=1}^N k^2
分式中的求和运算	$\frac{{\sum }_{k=1}^N{k}^2}{a}$	\frac{\sum_{k=1}^N k^2}{a}
分式中的求和运算	$\frac{\sum _{k=1}^N{k}^2}{a}$	\frac{\displaystyle \sum_{k=1}^N k^2}{a}
分式中的求和运算	$\frac{\sum _{k=1}^{{}^N}{k}^2}{a}$	\frac{\sum\limits^{^N}_{k=1} k^2}{a}
乘积运算	${\prod }_{i=1}^N{x}_i$	\prod_{i=1}^N x_i
乘积运算	${\prod }_{i=1}^N{x}_i$	\textstyle \prod_{i=1}^N x_i
副乘运算	${\coprod }_{i=1}^N{x}_i$	\coprod_{i=1}^N x_i
副乘运算	${\coprod }_{i=1}^N{x}_i$	\textstyle \coprod_{i=1}^N x_i
极限	${\lim }_{n\to \infty }{x}_n$	\lim_{n \to \infty}x_n
极限	${\lim }_{n\to \infty }{x}_n$	\textstyle \lim_{n \to \infty}x_n
积分	$\underset{1}{\overset{3}{\int }}\frac{e^3/x}{x^2}dx$	\int\limits_{1}^{3}\frac{e^3/x}{x^2}\, dx
积分	${\int }_1^3\frac{e^3/x}{x^2}dx$	\int_{1}^{3}\frac{e^3/x}{x^2}\, dx
积分	$\underset{-N}{\overset{N}{\int }}{e}^{x}dx$	\textstyle \int\limits_{-N}^{N} e^x dx
积分	${\int }_{-N}^N{e}^{x}dx$	\textstyle \int_{-N}^{N} e^x dx
双重积分	$\underset{D}{\iint }dxdy$	\iint\limits_D dx\,dy
三重积分	$\underset{E}{\iiint }dxdydz$	\iiint\limits_E dx\,dy\,dz
四重积分	$\int \underset{F}{\iiint }dxdydzdt$	\iiiint\limits_F dx\,dy\,dz\,dt
路径积分	${\int }_{(x,y)\in C}{x}^{3}dx+4y^{2}dy$	\int_{(x,y)\in C} x^3\, dx + 4y^2\, dy
环路积分	${\oint }_{(x,y)\in C}{x}^{3}dx+4y^{2}dy$	\oint_{(x,y)\in C} x^3\, dx + 4y^2\, dy
交集	${\bigcap }_{i=1}^n{E}_i$	\bigcap_{i=1}^n E_i
并集	${\bigcup }_{i=1}^n{E}_i$	\bigcup_{i=1}^n E_i

二项式系数

类型	符号	LaTeX
二项式系数	$\left(\genfrac{}{}{0ex}{}{n}{k}\right)$	\binom{n}{k}
小型二项式系数	$\left(\genfrac{}{}{0ex}{}{n}{k}\right)$	\tbinom{n}{k}
大型二项式系数	$\left(\genfrac{}{}{0ex}{}{n}{k}\right)$	\dbinom{n}{k}

矩阵

$$\begin{array}{cc}x& y\\ z& v\end{array}$$

\begin{matrix}
x & y \\
z & v
\end{matrix}

$$\left|\begin{array}{cc}x& y\\ z& v\end{array}\right|$$

\begin{vmatrix}
x & y \\
z & v
\end{vmatrix}

$$\Vert \begin{array}{cc}x& y\\ z& v\end{array}\Vert$$

\begin{Vmatrix}
x & y \\
z & v
\end{Vmatrix}

$$\left[\begin{array}{ccc}0& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & 0\end{array}\right]$$

\begin{bmatrix}
0 & \cdots & 0 \\
\vdots & \ddots & \vdots \\
0 & \cdots & 0
\end{bmatrix}

$$\left\{\begin{array}{cc}x& y\\ z& v\end{array}\right\}$$

\begin{Bmatrix}
x & y \\
z & v
\end{Bmatrix}

$$\left(\begin{array}{cc}x& y\\ z& v\end{array}\right)$$

\begin{pmatrix}
x & y \\
z & v
\end{pmatrix}

$$\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$$

\bigl( \begin{smallmatrix}
a&b\\
c&d
\end{smallmatrix} \bigr)

数组

$$\begin{array}{ccc}a& b& S\\ 0& 0& 1\\ 0& 1& 1\\ 1& 0& 1\\ 1& 1& 0\end{array}$$

\begin{array}{ | c | c | c | }
a & b & S \\
\hline
0 & 0 & 1 \\
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}

方程与方程组

$$\{\begin{array}{l}3x+5y+z\\ 7x-2y+4z\\ -6x+3y+2z\end{array}$$

\begin{cases}
3x + 5y + z \\
7x - 2y + 4z \\
-6x + 3y + 2z
\end{cases}

条件定义

$$f(n)=\{\begin{array}{ll}n/2,& \text{if }n\text{ is even}\\ 3n+1,& \text{if }n\text{ is odd}\end{array}$$

f(n) =
\begin{cases}
n/2, & \text{if }n\text{ is even} \\
3n+1, & \text{if }n\text{ is odd}
\end{cases}

多行等式

$$\begin{array}{rl}f(x)& =(a+b{)}^2\\ & =a^2+2ab+b^2\end{array}$$

\begin{align}
f(x) & = (a+b)^2\\
& = a^2+2ab+b^2
\end{align}

$$\begin{array}{rl}f(x)& =(a-b{)}^2\\ & =a^2-2ab+b^2\end{array}$$

\begin{alignat}{2}
f(x) & = (a-b)^2 \\
& = a^2-2ab+b^2
\end{alignat}

$$\begin{array}{lcl}z& =& a\\ f(x,y,z)& =& x+y+z\end{array}$$

\begin{array}{lcl}
z & = & a \\
f(x,y,z) & = & x + y + z
\end{array}

$$\begin{array}{lcr}z& =& a\\ f(x,y,z)& =& x+y+z\end{array}$$

\begin{array}{lcr}
z & = & a \\
f(x,y,z) & = & x + y + z
\end{array}

自动编号

开启 AMS 扩展包的情况下，会在部分环境的多行公式后自动编号；

KaTeX parse error: No such environment: eqnarray at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲ E = mc^2 \\ e^…

\begin{eqnarray}
E = mc^2 \\
e^{i\pi}+1=0
\end{eqnarray}

KaTeX parse error: No such environment: eqnarray* at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲*̲}̲ E = mc^2 \\ e^…

\begin{eqnarray*}
E = mc^2 \\
e^{i\pi}+1=0
\end{eqnarray*}

KaTeX parse error: No such environment: eqnarray at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲ E = mc^2 \\ e^…

\begin{eqnarray}
E = mc^2 \\
e^{i\pi}+1=0 \nonumber
\end{eqnarray}

KaTeX parse error: No such environment: eqnarray at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲ E = mc^2 \nota…

\begin{eqnarray}
E = mc^2 \notag\\
e^{i\pi}+1=0 \tag{b}
\end{eqnarray}

括号

常用的 ()、[]、{} 括号符号可以在 LaTeX 环境当中直接进行使用，但是如果处于较大的符号当中，就应该配合 \left 与 \right 命令来使用：

类型	符号	LaTeX
圆括号、小括号	(ab)	\left ( \frac{a}{b} \right )
方括号、中括号	$\left[\frac{a}{b}\right]$ $\left[\frac{a}{b}\right]$	\left [ \frac{a}{b} \right ] \left \lbrack \frac{a}{b} \right \rbrack
花括号、大括号	$\left\{\frac{a}{b}\right\}$ $\left\{\frac{a}{b}\right\}$	\left \{ \frac{a}{b} \right \} \left \lbrace \frac{a}{b} \right \rbrace
角括号	$⟨\frac{a}{b}⟩$	\left \langle \frac{a}{b} \right \rangle
单竖线和双竖线	$\left|\frac{a}{b}\right|$ $\Vert \frac{c}{d}\Vert$	\left \vert \frac{a}{b} \right \vert \left \Vert \frac{c}{d} \right \Vert
取整函数与取顶函数	$\lfloor \frac{a}{b}\rfloor$ $\lceil \frac{c}{d}\rceil$	\left \lfloor \frac{a}{b} \right \rfloor \left \lceil \frac{c}{d} \right \rceil
斜线与反斜线	$/\frac{a}{b}\backslash$	\left / \frac{a}{b} \right \backslash
上下箭头	$\uparrow \frac{a}{b}\downarrow$ $\Uparrow \frac{a}{b}\Downarrow$ $\updownarrow \frac{a}{b}\Updownarrow$	\left \uparrow \frac{a}{b} \right \downarrow \left \Uparrow \frac{a}{b} \right \Downarrow \left \updownarrow \frac{a}{b} \right \Updownarrow
混合括号	[0,1) ⟨ψ|	\left [ 0,1 \right ) \left \langle \psi \right \vert
使用\left.和\right.不显示某侧的括号；	$$\frac{A}{B}\}\to X$$	\left. \frac{A}{B} \right \} \to X

注意：在 Markdown 当中使用 LaTeX 时，为了避免语法冲突，花括号 {} 必须采用 \{和\} 进行转义，或者改用 \lbrace 和 \rbrace 的方式；如果是在 Markdown 表格当中使用 LaTeX，则必须采用 \vert 或者 \Vert 代替直接在公式当中书写 | 和 ||。

括号尺寸

符号	LaTeX
$((\left(\right((\dots ]\left]\right]]]$	( \bigl( \Bigl( \biggl( \Biggl( \dots \Biggr] \biggr] \Bigr] \bigr] ]
{ { { { { …   ⟩ ⟩ ⟩ ⟩ ⟩ \{ \bigl \{ \Bigl \{ \biggl \{ \Biggl \{ \dots \Biggr\rangle \biggr\rangle \Bigr\rangle \bigr\rangle \rangle {{{{{…⟩⟩⟩⟩⟩	\{ \bigl \{ \Bigl \{ \biggl \{ \Biggl \{ \dots \Biggr\rangle \biggr\rangle \Bigr\rangle \bigr\rangle \rangle
$||\left|\right||\dots |\left|\right||$	\vert \big \vert \Big \vert \bigg \vert \Bigg \vert \dots \Bigg \vert \bigg \vert \Big \vert \big \vert
$\lfloor \lfloor \lfloor \lfloor \lfloor \dots \rceil \rceil \rceil \rceil \rceil$	\lfloor \bigl\lfloor \Bigl\lfloor \biggl\lfloor \Biggl\lfloor \dots \Biggr\rceil \biggr\rceil \Bigr\rceil \bigr\rceil \rceil
$$\uparrow \uparrow \uparrow \uparrow \uparrow \dots \Downarrow \Downarrow \Downarrow \Downarrow \Downarrow$$	\uparrow \big\uparrow \Big\uparrow \bigg\uparrow \Bigg\uparrow \dots \Bigg\Downarrow \bigg\Downarrow \Big\Downarrow \big\Downarrow \Downarrow
$\updownarrow \updownarrow \updownarrow \updownarrow \updownarrow \dots \Updownarrow \Updownarrow \Updownarrow \Updownarrow \Updownarrow$	\updownarrow \big\updownarrow \Big\updownarrow \bigg\updownarrow \Bigg\updownarrow \dots \Bigg\Updownarrow \bigg\Updownarrow \Big\Updownarrow \big\Updownarrow \Updownarrow
$/////\dots \backslash \backslash \backslash \backslash \backslash$	/ \big/ \Big/ \bigg/ \Bigg/ \dots \Bigg\backslash \bigg\backslash \Big\backslash \big\backslash \backslash

空格与换行

序号	符号	LaTeX
双空格	$ab$	a \qquad b
单空格	$ab$	a \quad b
字符空格	$ab$	a\ b
文本模式中的字符空格	$ab$	a \text{ } b
大空格	$ab$	a\;b
小空格	$ab$	a\,b
极小空格	$ab$	ab
极小空格（用于区分语法）	$ab$	a b
无空格（用于区分多字母变量）	$ab$	\mathit{ab}

MathJax 3.0 取消了单行公式环境下 \\ 的强制换行功能，因此强制换行命令 \\ 仅能用于 eqnarray、align、array、matrix 等多行环境当中。除此之外，还可以在 \displaylines{} 行显示命令当中使用 \\ 强制换行命令：

符号	LaTeX
KaTeX parse error: Undefined control sequence: \displaylines at position 1: \̲d̲i̲s̲p̲l̲a̲y̲l̲i̲n̲e̲s̲{y=1729x \\ y=1…	\displaylines{y=1729x \\ y=1729-x}

颜色

注意：CSDN中Markdown使用KaTex支持LeTeX，如下颜色列表，KaTex好多不支持，建议使用16进制。

编写 LaTeX 的时候，支持将文本、符号或者背景设置为下面表格当中的各种颜色：
$example$

$\textcolor{red}{example}$
$\color{red}{example}$
$\color{00FF00}{example}$

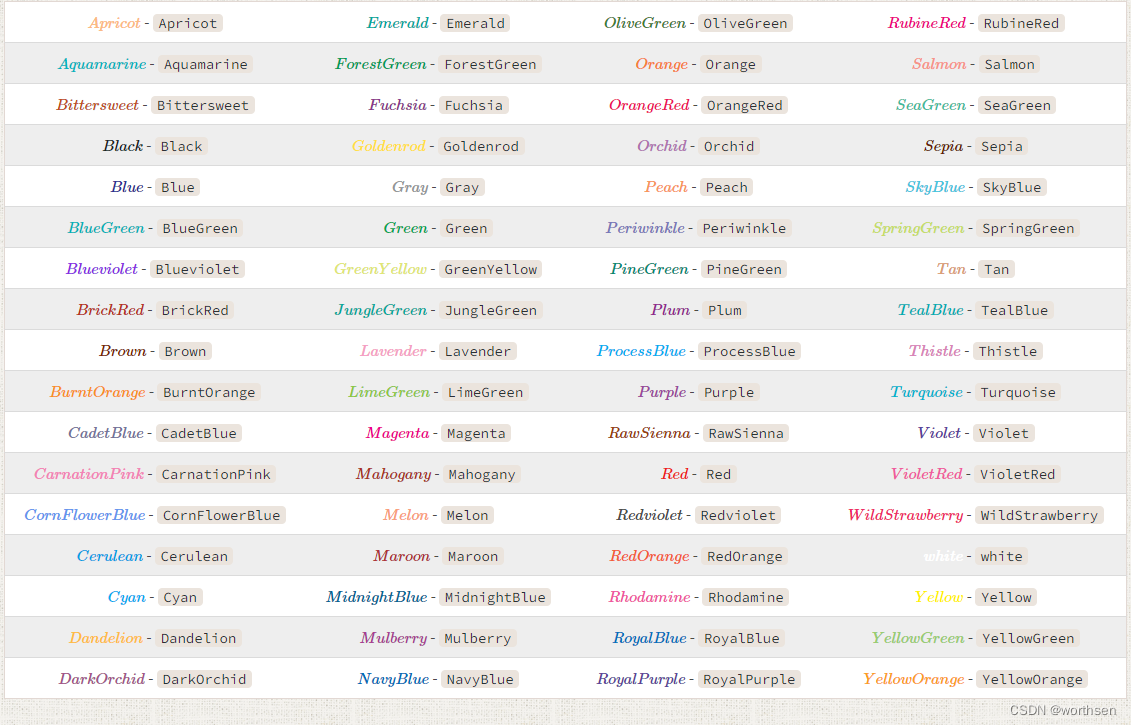
Apricot - Apricot	Emerald - Emerald	OliveGreen - OliveGreen	RubineRed - RubineRed
Aquamarine - Aquamarine	ForestGreen - ForestGreen	Orange - Orange	Salmon - Salmon
Bittersweet - Bittersweet	Fuchsia - Fuchsia	OrangeRed - OrangeRed	SeaGreen - SeaGreen
Black - Black	Goldenrod - Goldenrod	Orchid - Orchid	Sepia - Sepia
Blue - Blue	Gray - Gray	Peach - Peach	SkyBlue - SkyBlue
BlueGreen - BlueGreen	Green - Green	Periwinkle - Periwinkle	SpringGreen - SpringGreen
Blueviolet - Blueviolet	GreenYellow - GreenYellow	PineGreen - PineGreen	Tan - Tan
BrickRed - BrickRed	JungleGreen - JungleGreen	Plum - Plum	TealBlue - TealBlue
Brown - Brown	Lavender - Lavender	ProcessBlue - ProcessBlue	Thistle - Thistle
BurntOrange - BurntOrange	LimeGreen - LimeGreen	Purple - Purple	Turquoise - Turquoise
CadetBlue - CadetBlue	Magenta - Magenta	RawSienna - RawSienna	Violet - Violet
CarnationPink - CarnationPink	Mahogany - Mahogany	Red - Red	VioletRed - VioletRed
CornFlowerBlue - CornFlowerBlue	Melon - Melon	Redviolet - Redviolet	WildStrawberry - WildStrawberry
Cerulean - Cerulean	Maroon - Maroon	RedOrange - RedOrange	white - white
Cyan - Cyan	MidnightBlue - MidnightBlue	Rhodamine - Rhodamine	Yellow - Yellow
Dandelion - Dandelion	Mulberry - Mulberry	RoyalBlue - RoyalBlue	YellowGreen - YellowGreen
DarkOrchid - DarkOrchid	NavyBlue - NavyBlue	RoyalPurple - RoyalPurple	YellowOrange - YellowOrange

字体颜色

公式当中可以使用 {\color{hues}text} 调用颜色命令，其中 hues 参数为字体颜色，而 text 参数是公式内容：

符号	LaTeX
$x^2+2x-1$	{\color{Blue}x^2}+{\color{Orange}2x}-{\color{LimeGreen}1}

背景颜色

文本环境中可以使用 \colorbox{hues}{text} 来调用背景颜色命令，其中 hues 参数为背景颜色，而 text 参数是公式内容：

符号	LaTeX
$Thistext$	\colorbox{yellow}{Thistext}

该命令应用于数学环境当中时，需要在第 2 个参数加入 $\displaystyle + 公式$：

符号	LaTeX
$$\frac{a}{b}$$	\colorbox{yellow}{$\displaystyle \frac{a}{b}$}

注意：在 Markdown 内联 LaTeX 公式 $...$ 当中使用 $\displaystyle + 公式$ 语法时将会引发冲突，因此该语法仅用于多行公式 $$...$$。

RGB 颜色

通过使用 \definecolor 命令可以自定义 LaTeX 公式的颜色：

符号	LaTeX
$$e^{i\pi }+1=0$$	\definecolor{mygreen}{RGB}{0,200,0} {\color{mygreen}e^{i \pi} + 1 = 0 }

csdn 的 markdown 使用如下
$$\textcolor{00FF00}{e^{i \pi} + 1 = 0}$$

字体

字体加粗

符号	LaTeX
$\mathbf{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$	\boldsymbol{ABCDEFGHIJKLMNOPQRSTUVWXYZ}
$\mathbf{abcdefghijklmnopqrstuvwxyz}$	\boldsymbol{abcdefghijklmnopqrstuvwxyz}
$0123456789$	\boldsymbol{0123456789}

黑体

符号	LaTeX
$\mathbf{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$	\mathbf{ABCDEFGHIJKLMNOPQRSTUVWXYZ}
$\mathbf{abcdefghijklmnopqrstuvwxyz}$	\mathbf{abcdefghijklmnopqrstuvwxyz}
$0123456789$	\mathbf{0123456789}

黑板报体

符号	LaTeX
$\mathbb{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$	\mathbb{ABCDEFGHIJKLMNOPQRSTUVWXYZ}
𝕒𝕓𝕔𝕕𝕖𝕗𝕘𝕙𝕚𝕛𝕜𝕝𝕞𝕟𝕠𝕡𝕢𝕣𝕤𝕥𝕦𝕧𝕨𝕩𝕪𝕫	\mathbb{abcdefghijklmnopqrstuvwxyz}
𝟘𝟙𝟚𝟛𝟜𝟝𝟞𝟟𝟠𝟡	\mathbb{0123456789}

斜体

符号	LaTeX
$ABCDEFGHIJKLMNOPQRSTUVWXYZ$	\mathit{ABCDEFGHIJKLMNOPQRSTUVWXYZ}
$abcdefghijklmnopqrstuvwxyz$	\mathit{abcdefghijklmnopqrstuvwxyz}
$0123456789$	\mathit{0123456789}

罗马体

符号	LaTeX
$\mathrm{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$	\mathrm{ABCDEFGHIJKLMNOPQRSTUVWXYZ}
$\mathrm{abcdefghijklmnopqrstuvwxyz}$	\mathrm{abcdefghijklmnopqrstuvwxyz}
$0123456789$	\mathrm{0123456789}

无衬线体

符号	LaTeX
$\mathsf{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$	\mathsf{ABCDEFGHIJKLMNOPQRSTUVWXYZ}
$\mathsf{abcdefghijklmnopqrstuvwxyz}$	\mathsf{abcdefghijklmnopqrstuvwxyz}
$0123456789$	\mathsf{0123456789}

手写体

符号	LaTeX
$\mathcal{A}\mathcal{BC}\mathcal{D}\mathcal{EFGH}\mathcal{I}\mathcal{J}\mathcal{K}\mathcal{LM}\mathcal{N}\mathcal{O}\mathcal{P}\mathcal{Q}\mathcal{R}\mathcal{S}\mathcal{T}\mathcal{U}\mathcal{V}\mathcal{W}\mathcal{X}\mathcal{Y}\mathcal{Z}$	\mathcal{ABCDEFGHIJKLMNOPQRSTUVWXYZ}
$abcdefghijklmnopqrstuvwxyz$	\mathcal{abcdefghijklmnopqrstuvwxyz}
$0123456789$	\mathcal{0123456789}

哥特字体

符号	LaTeX
$\mathfrak{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$	\mathfrak{ABCDEFGHIJKLMNOPQRSTUVWXYZ}
$\mathfrak{abcdefghijklmnopqrstuvwxyz}$	\mathfrak{abcdefghijklmnopqrstuvwxyz}
$0123456789$	\mathfrak{0123456789}

小脚本风格

符号	LaTeX
$\text{ABCDEFGHIJKLMNOPQRSTUVWXYZ}$	{\scriptstyle\text{ABCDEFGHIJKLMNOPQRSTUVWXYZ}}
$\text{abcdefghijklmnopqrstuvwxyz}$	{\scriptstyle\text{abcdefghijklmnopqrstuvwxyz}}
$\text{0123456789}$	{\scriptstyle\text{0123456789}}

字号尺寸

符号	LaTeX
$abc极小tiny$	{\tiny abc极小tiny}
$abc超小scriptsize$	{\scriptsize abc 超小 scriptsize}
$abc小small$	{\small abc 小 small}
$abc正常normal$	{\normalsize abc 正常 normal}
$abc大large$	{\large abc 大 large}
$abc超大Large$	{\Large abc 超大 Large}
$abc特大LARGE$	{\LARGE abc 特大 LARGE}
$abc巨大huge$	{\huge abc 巨大 huge}
$abc巨无霸Huge$	{\Huge abc 巨无霸 Huge}

参考

1、官方–latex
2、官方–katex
2、通用 LaTeX 数学公式语法手册