leetcode63. 不同路径 II

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/unique-paths-ii

题目描述

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？
网格中的障碍物和空位置分别用 1 和 0 来表示。

示例1:

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：

向右 -> 向右 -> 向下 -> 向下
向下 -> 向下 -> 向右 -> 向右

示例2:

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1

暴力递归

这题是leetcode62. 不同路径的拓展版.加了障碍物,解题思路是一样的,只是要加下障碍物的判断.
还是向下和向右两个方向的选择,两种情况的和就是所有的路线数.

代码演示

/**
* 主方法
*/
 public int uniquePathsWithObstacles(int[][] obstacleGrid) {
 	//如果右下角是障碍物,怎么都过不去,直接返回0
        if(obstacleGrid[obstacleGrid.length - 1][obstacleGrid[0].length - 1] == 1){
            return 0;
        }
        //开始递归
        return process(obstacleGrid,0,0);
    }
	/**
	* 暴力递归
	* i 和 j 描述当前在的位置
	*/
    public int process(int[][]obstacleGrid,int i,int j){
    	//base case 来到最后一个位置,前面路线有效,返回1
        if(i == obstacleGrid.length - 1 && j == obstacleGrid[0].length - 1 ){
            return 1;
        }
        //越界,路线无效 返回0
        if(i >= obstacleGrid.length || j >= obstacleGrid[0].length){
            return 0;
        }
        // 碰到障碍物,无效返回0
        if(obstacleGrid[i][j] == 1){
            return 0;
        }
        //x向下和向右两种情况
        int down = process(obstacleGrid,i + 1,j);
        int right = process(obstacleGrid,i,j + 1);
        //两种情况累加就是所有的路线
        return down + right;
    }

动态规划

从暴力递归中可以得知,(i,j) 位置依赖 (i+1,j)和(i,j+1)两个位置,所以可以轻松得到状态转移方程是:

f(i,j) = f(i+1,j) + f(i,j+1;
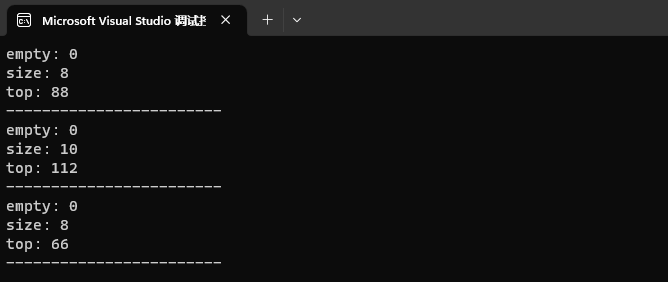
但这里有一些需要注意的地方,就是障碍物的处理,和dp表的初始化,我们以图为例:

上面图代表要走的网格,我只填写了最后一行和一列其他位置没有标注,因为现在只讨论最后一行和一列的情况.
最后一行为例,三角符号标注的位置是最后一次出现的障碍物,在这个障碍物之前的最后一行位置,都无法到最后位置了,所以之前的位置在dp 表中要初始化为0,之后的可以初始化为1,
最后一列也是同样情况:
下面看下代码中如何处理;

代码演示

  /**
     * 动态规划
     * @param obstacleGrid
     * @return
     */
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int n = obstacleGrid.length;
        int m = obstacleGrid[0].length;
        //最有下角如果是障碍物,就无法过去,返回 0
        if (obstacleGrid[n - 1][m - 1] == 1) {
            return 0;
        }
        //动态规划表
        int[][]dp = new int[n][m];
        //来标记最后一行最后一次出现障碍物的位置
        int flagN = -1;
        //来标记最后一列最后一次出现障碍物的位置
        int flagM = -1;
        for (int i = m - 1; i >= 0;i--){
            if(obstacleGrid[n - 1][i] == 1){
                flagN = i;
                break;
            }
        }
        //最后一个障碍物之后的位置初始化为1
        for (int i = flagN + 1; i < m;i++){
            dp[n - 1][i] = 1;
        }
        //标记最后一列最后一次出现障碍物的位置.
        for (int j =  n - 1; j >= 0;j--){
            if(obstacleGrid[j][m - 1] == 1){
                flagM = j;
                break;
            }
        }
        //最后一个障碍物之后的位置初始化为1
        for (int j = flagM + 1; j < n;j++){
            dp[j][m - 1] = 1;
        }

        for (int i = n - 2;i >= 0;i--){
            for (int j = m - 2;j >= 0;j--){
                //当前位置本身是障碍物 即为0
                if(obstacleGrid[i][j] == 1){
                    dp[i][j] = 0;
                }else{
                    //z状态转移方程
                    dp[i][j] = dp[i + 1][j] + dp[i][j + 1];
                }

            }
        }
        return dp[0][0];
    }

动态规划空间压缩

  /**
     * 动态规划 + 空间压缩
     * @param obstacleGrid
     * @return
     */
    public int uniquePathsWithObstacles2(int[][] obstacleGrid) {
        int n = obstacleGrid.length;
        int m = obstacleGrid[0].length;
        if (obstacleGrid[n - 1][m - 1] == 1) {
            return 0;
        }
        int[]dp = new int[m];
        int flagN = -1;
        for (int i = m - 1; i >= 0;i--){
            if(obstacleGrid[n - 1][i] == 1){
                flagN = i;
                break;
            }
        }
        for (int i = flagN + 1; i < m;i++){
            dp[i] = 1;
        }
        int flagM = -1;
        for (int j =  n - 1; j >= 0;j--){
            if(obstacleGrid[j][m - 1] == 1){
                flagM = j;
                break;
            }
        }

        for (int i = n - 2;i >= 0;i--){
            dp[m - 1] = i > flagM ? 1 : 0;
            for (int j = m - 2;j >= 0;j--){
                if(obstacleGrid[i][j] == 1){
                    dp[j] = 0;
                }else{
                    dp[j] = dp[j] + dp[j + 1];
                }

            }
        }
        return dp[0];
    }