贪婪算法是一种算法范例，它遵循在每个阶段进行局部最优选择的问题求解启发式，希望找到全局最优值。换句话说，贪婪算法在每一步都选择最好的可能选项，而不考虑该选择对未来步骤的影响。

当一个问题可以被划分成更小的子问题，并且每个子问题的解可以被组合以解决整个问题时，贪婪算法是有用的。贪婪算法可用于解决涉及在许多可能的解中找到最佳解的优化问题。
可以使用贪婪算法解决的问题的经典示例是“硬币找零”问题。问题是用尽可能少的硬币换给定金额的钱。例如，如果金额是25美分，可用的硬币是1美分，5美分和10美分，那么贪婪算法将在每一步选择最大的硬币。它会先选择一个10美分的硬币，然后是另一个10美分的硬币，最后是一个5美分的硬币，总共有三个硬币。
然而，贪婪算法可能并不总是找到最优解。例如，如果可用的硬币是1美分、3美分和4美分，并且金额是6美分，则贪婪算法将选择一个4美分硬币和两个1美分硬币，而最优解决方案是使用两个3美分硬币。

因此，证明贪婪算法的正确性并理解其局限性是很重要的。贪婪算法可以应用于许多环境中，包括调度、图论和动态规划。
贪婪算法被定义为一种解决优化问题的方法，它通过采取决策来产生最明显和最直接的利益，而不管最终结果如何。它适用于最小化或最大化导致所需解决方案的情况。

贪婪算法的特点

对于要使用贪婪方法解决的问题，它必须遵循以下几个主要特征：

• 有一个有序的资源列表（利润、成本、价值等）
• 所有资源的最大值（最大利润、最大价值等）都有了
• 例如，在分数背包问题中，根据可用容量首先取最大值/权重。
  

使用贪婪算法

贪婪算法是一种用于优化问题的方法，其目标是在每个阶段进行局部最优选择，并希望找到全局最优值。它被称为“贪婪”，因为它试图通过在每一步做出最佳选择来找到最佳解决方案，而不考虑未来的步骤或当前决策的后果。
贪婪算法的一些常见用例包括：
调度和资源分配：贪婪算法可以用于调度作业或以有效的方式分配资源。
最小生成树：贪婪算法可以用来寻找图的最小生成树，它是连接所有顶点的总边权最小的子图。
硬币兑换问题：贪婪算法可以用于通过总是选择具有小于要改变的剩余量的最高值的硬币来以最小数量的硬币对给定量进行改变。
霍夫曼编码：贪婪算法可用于生成用于数据压缩的无前缀代码，通过以考虑每个字符的频率的方式构造二叉树。

值得注意的是，并不是所有的优化问题都可以用贪婪算法来解决，在某些情况下，贪婪方法可能会导致次优解决方案。然而，在许多情况下，贪婪算法提供了一个很好的近似最优解，是一个有用的工具，快速有效地解决优化问题。

所有贪婪算法都遵循一个基本结构

1. 声明一个空结果 = 0。
2. 我们做一个贪婪的选择，如果选择是可行的，把它添加到最终结果。
3. 返回结果。

为什么选择贪婪算法？

贪婪方法具有一些折衷，这可以使其适合于优化。一个突出的原因是立即获得最可行的解决方案。在活动选择问题中（下面解释），如果在完成当前活动之前可以完成更多活动，则这些活动可以在相同的时间内执行。 另一个原因是基于条件递归地划分问题，而不需要联合收割机所有的解决方案。在活动选择问题中，“递归除法”步骤通过仅扫描一次项目列表并考虑某些活动来实现。

贪婪算法示例

具有最优子结构性质并可使用贪婪方法求解的一些著名问题是

1. 作业排序问题：
   贪婪地首先选择利润最大的工作，通过将工作按其利润的降序排序。这将有助于最大化总利润，因为选择每个时间段利润最大的作业最终将使总利润最大化
2. 求最小生成树的Prim算法：
   它从一个空的生成树开始。这个想法是维护两组顶点。第一集合包含已经包括在MST中的顶点，另一集合包含尚未包括的顶点。在每一步，它考虑连接两个集合的所有边，并从这些边中挑选最小权重边。拾取边后，它将边的另一个端点移动到包含MST的集合。

贪婪算法是如何工作的？

当在没有进行彻底检查的情况下选择应用贪婪方法时，使用它的决定可能会有些困难，有时甚至会导致失败。在某些情况下，采用局部最佳选择可能导致失去全局最优解。
例如：

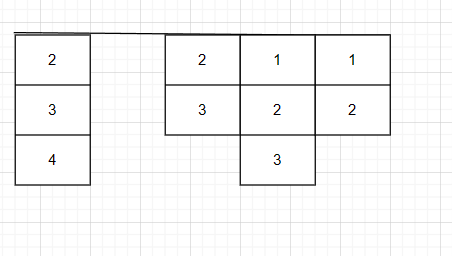
• 贪婪方法失败的一个这样的示例是找到给定图中的节点的最大加权路径。
  
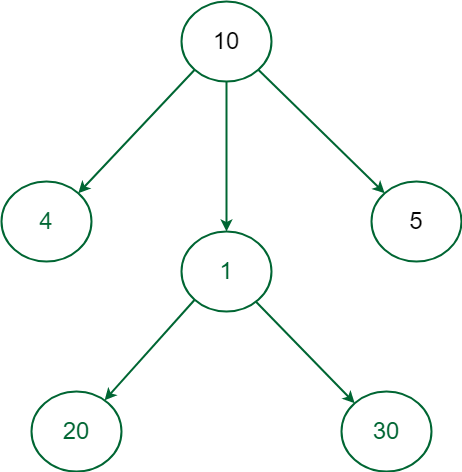
• 在上图中，从根节点10开始，如果我们贪婪地选择下一个节点以获得最大权重路径，则下一个选择的节点将是5，其将取总和为15，并且路径将结束，因为不存在5的子节点，但是路径10 -> 5不是最大权重路径。
  
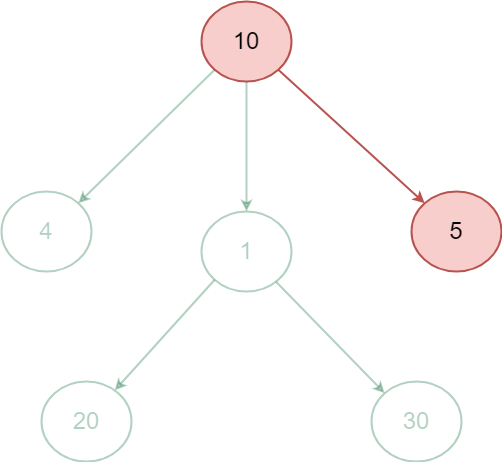
• 为了找到最大权的路径，必须计算所有可能的路径和，并且必须比较它们的路径和以得到期望的结果，可见，上图中的最大权的路径是10 -> 1 -> 30，其给出路径和41。
  
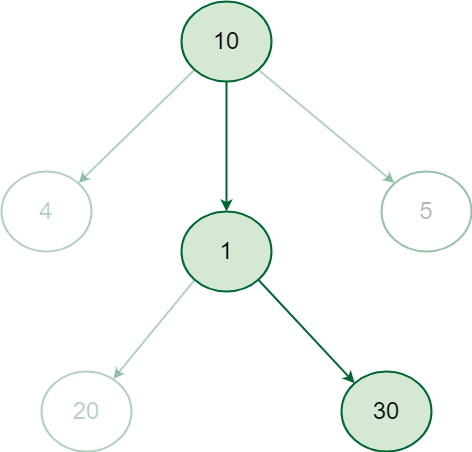
• 在这种情况下，贪婪方法将不起作用，而是必须考虑从根到叶节点的完整路径以获得正确的答案，即。这可以通过递归地检查所有路径并计算它们的权重来实现。

因此，使用贪婪算法的问题必须不包含重叠的子问题。

贪婪算法的应用

• 寻找最佳解决方案（活动选择，分数背包，作业排序，霍夫曼编码）。
• 找到接近最优解的NP难题，如TSP。
• 贪婪算法用于选择在各自的截止日期之前完成的作业，并使利润最大化。
• 贪婪算法用于基于某些标准（例如距离或相似性）将数据点聚类在一起。
• 问题被分解为独立解决的更小的子问题，但这些子问题中的许多是相同或重叠的。

贪婪算法的优点

• 贪婪算法很容易实现。
• 通常具有较低的时间复杂度。
• 贪婪算法可以用于优化目的或在困难问题的情况下找到接近优化的结果。
• 贪婪算法可能非常有效，因为它不需要探索问题的所有可能解决方案。
• 贪婪算法可以为问题提供清晰且易于理解的解决方案，因为它遵循一个循序渐进的过程。
• 子问题的解决方案可以存储在一个表中，该表可以重复用于类似的问题。

贪婪算法的缺点

• 局部最优解可能不总是全局最优的。
• 缺乏最优性证明。
• 贪婪算法仅适用于具有贪婪选择属性的问题，这意味着并非所有问题都可以使用这种方法来解决。
• 贪婪算法不容易适应不断变化的问题条件。

以下是使用贪婪算法时需要记住的一些要点

1. 贪婪算法在每一步都做出局部最优选择，而不考虑该选择对未来步骤的影响。
2. 贪婪算法可以用来解决优化问题，可以分为更小的子问题。
3. 贪婪算法可能并不总是找到最优解。证明贪婪算法的正确性并理解其局限性是很重要的。
4. 贪婪算法可以应用于许多环境中，包括调度、图论和动态编程。
5. 在设计贪婪算法时，确定最优子结构和贪婪选择性质是很重要的。
6. 贪婪算法的时间复杂度取决于具体问题和算法的实现。
7. 贪婪算法有时可以作为一种启发式方法来解决问题时，很难找到最优解在实践中。

在一些情况下，贪婪算法可以提供接近最优解的解，但不一定是精确的最优解。这些解称为近似解。