堆:
一种满足特定条件的完全二叉树,可分为两种类型:
- 「大顶堆 Max Heap」,任意节点的值 ≥其子节点的值;
- 「小顶堆 Min Heap」,任意节点的值 ≤ 其子节点的值;

将二叉树的根节点称为「堆顶」,将底层最靠右的节点称为「堆底」。
知识点一、堆常用操作
堆通常用作实现优先队列,大顶堆相当于元素按从大到小顺序出队的优先队列。从使用角度来看,我们可以将「优先队列」和「堆」看作等价的数据结构。

大顶堆在入栈的时候*-1颠倒大小关系,max_heap[0]是最小的数(负数形式),取出的时候再乘回-1,变成正数,是最大的数
# 输入列表并建堆
min_heap: List[int] = [1, 3, 2, 5, 4]
heapq.heapify(min_heap)知识点二、堆的实现
1.堆的储存:
堆由于满足完全二叉树,所以很适合用数组储存(地址连续)当使用数组表示二叉树时,元素代表节点值,索引代表节点在二叉树中的位置。节点指针通过索引映射公式来实现。
给定索引i,其父节点为(i-1)//2,左子节点为2i+1,右子节点为2i+2
堆顶元素:max_heap[0]
2.元素入堆:O(logn)
给定元素 val ,我们首先将其添加到堆底。添加之后,由于 val 可能大于堆中其他元素,堆的成立条件可能已被破坏。因此,需要修复从插入节点到根节点的路径上的各个节点,这个操作被称为「堆化 Heapify」。
考虑从入堆节点开始,从底至顶执行堆化。具体来说,我们比较插入节点与其父节点的值,如果插入节点更大,则将它们交换。然后继续执行此操作,从底至顶修复堆中的各个节点,直至越过根节点或遇到无需交换的节点时结束。

3.堆顶元素出堆 O(logn)
堆顶元素是二叉树的根节点,即列表首元素。
为了尽量减少元素索引的变动,采取以下操作步骤:
- 交换堆顶元素与堆底元素(即交换根节点与最右叶节点);
- 交换完成后,将堆底从列表中删除(注意,由于已经交换,实际上删除的是原来的堆顶元素);
- 从根节点开始,从顶至底执行堆化(将根节点的值与其两个子节点的值进行比较,将最大的子节点与根节点交换;然后循环执行此操作,直到越过叶节点或遇到无需交换的节点时结束。);
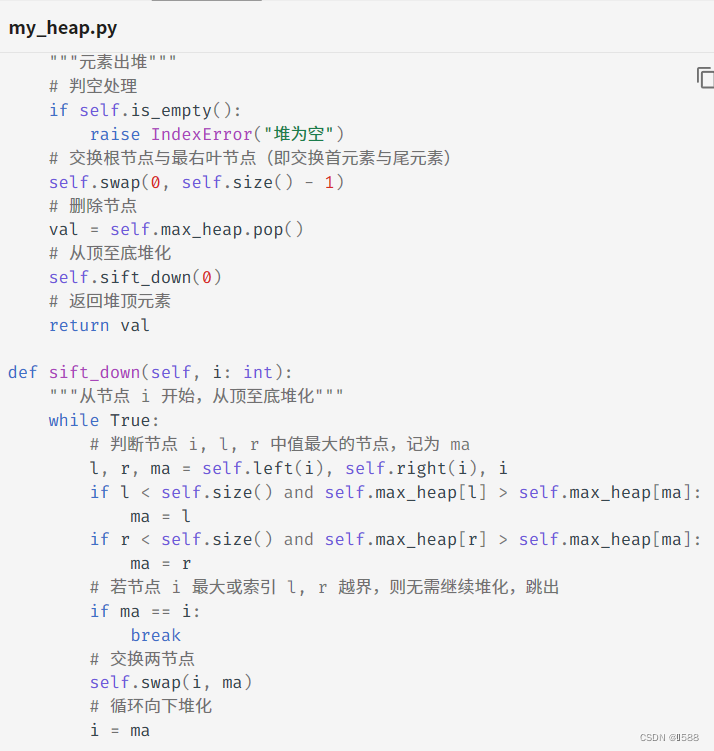
swap那里换的是i和ma索引对应的值,但是i和ma这两个索引没变,后面i=ma才是相当于把指针(索引)挪到子节点处,让i和ma指向同一个子节点
知识点三、建堆操作:根据输入列表生成一个堆
方法1.首先创建一个空堆,然后将列表元素依次添加到堆中。O(nlogn)
方法2.先将列表所有元素原封不动添加到堆中,然后迭代地对各个节点执行“从顶至底堆化” 优化至O(n)
知识点四、用堆解决Top-K问题:
- 初始化一个小顶堆,其堆顶元素最小;
- 先将数组的前 k 个元素依次入堆;
- 从第 k + 1 个元素开始,若当前元素大于堆顶元素,则将堆顶元素出堆,并将当前元素入堆;
- 遍历完成后,堆中保存的就是最大的 k 个元素;
O(nlogk)

有一个问题,在heappush之后,是不是应该heapify一下?还是说这里默认删除和插入都会附带heapify?