字符          数值
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

例如， 罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做  XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

• I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
• X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。 
• C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给你一个整数，将其转为罗马数字。

 

示例 1:

输入: num = 3
输出: "III"

示例 2:

输入: num = 4
输出: "IV"

示例 3:

输入: num = 9
输出: "IX"

示例 4:

输入: num = 58
输出: "LVIII"
解释: L = 50, V = 5, III = 3.

示例 5:

输入: num = 1994
输出: "MCMXCIV"
解释: M = 1000, CM = 900, XC = 90, IV = 4.

 

提示：

• 1 <= num <= 3999

题解
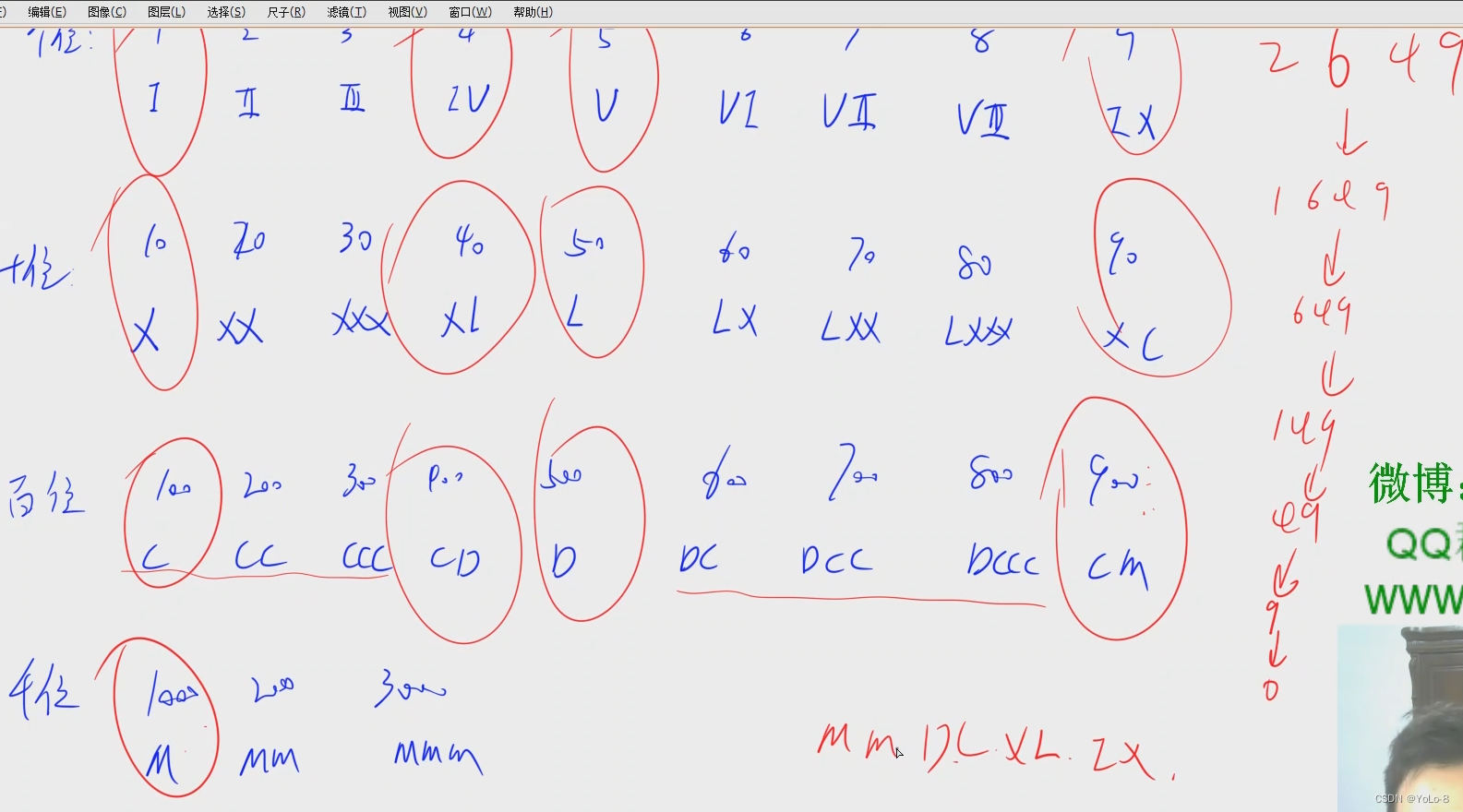
找规律
从一般到特殊

class Solution {
public:
    string intToRoman(int num) {
        int values[] = {
            1000,
            900,500,400,100,
            90,50,40,10,
            9,5,4,1,
        };
        string reps[] = {
            "M",
            "CM","D","CD","C",
            "XC","L","XL","X",
            "IX","V","IV","I",
        };
        string res;
        for(int i = 0; i <= 12;i++){
            while(num >= values[i]) {
                num -= values[i];
                res += reps[i];
            }
        }
        return res;
    }
};