子集型回溯

在这里插入图片描述
主要学习分别从输入和答案去思考的两种代码模板。

例题1——78.子集

例题：78. 子集
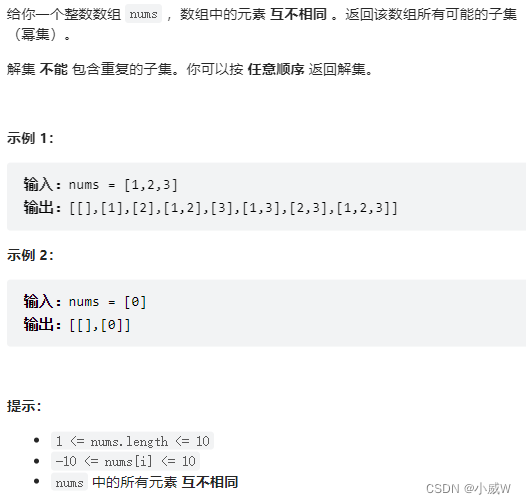
在这里插入图片描述

代码模板1

站在答案的角度思考
枚举第一个数选谁
枚举第二个数选谁
每个节点都是答案

class Solution {
    List<List<Integer>> ans = new ArrayList();
    List<Integer> t = new ArrayList();

    public List<List<Integer>> subsets(int[] nums) {
        dfs(0, nums);
        return ans;
    }

    public void dfs(int startIndex, int[] nums) {
        ans.add(new ArrayList(t));
        if (startIndex == nums.length) {
            return;
        }
        for (int i = startIndex; i < nums.length; ++i) {
            t.add(nums[i]);
            dfs(i + 1, nums);
            t.remove(t.size() - 1);
        }
    }
}

代码模板2

站在输入的角度思考
每个数可以在子集中（选）
也可以不在子集中（不选）
叶子是答案

class Solution {
    List<List<Integer>> ans = new ArrayList();
    List<Integer> t = new ArrayList();

    public List<List<Integer>> subsets(int[] nums) {
        dfs(0, nums);
        return ans;
    }

    public void dfs(int i, int[] nums) {
        if (i == nums.length) {
            ans.add(new ArrayList(t));	// 当每个位置都经历了选和不选之后，加入答案
            return;
        }
        dfs(i + 1, nums);	// 不选直接下一个
        t.add(nums[i]);
        dfs(i + 1, nums);	// 选了之后递归下一个
        t.remove(t.size() - 1);
    }
}

个人感觉代码模板2更好理解一些。

例题2——131.分割回文串

https://leetcode.cn/problems/palindrome-partitioning/
在这里插入图片描述

所谓分割字符串，其实就是字符之间的逗号选不选的问题，因此这也是子集型回溯。

代码模板1

class Solution {
    boolean[][] st;
    List<List<String>> ans = new ArrayList();
    List<String> t = new ArrayList();

    public List<List<String>> partition(String s) {
        int n = s.length();
        st = new boolean[n][n];		// 提前计算出dp[i][j]表示从i~j是否为回文串
        for (int i = n - 1; i >= 0; --i) {
            for (int j = i; j < n; ++j) {
                if (i == j) st[i][j] = true;
                else if (j == i + 1) st[i][j] = s.charAt(i) == s.charAt(j);
                else st[i][j] = st[i + 1][j - 1] && s.charAt(i) == s.charAt(j);
            }
        }
        dfs(s, 0);
        return ans;
    }

    public void dfs(String s, int startIndex) {
        if (startIndex == s.length()) {
            ans.add(new ArrayList(t));
            return;
        }
        for (int i = startIndex; i < s.length(); ++i) {
            if (st[startIndex][i]) {	// 从startIndex到当前i是回文串
                t.add(s.substring(startIndex, i + 1));
                dfs(s, i + 1);
                t.remove(t.size() - 1);
            }
        }
    }
}

代码模板2

class Solution {
    List<List<String>> ans = new ArrayList();
    List<String> t = new ArrayList();

    public List<List<String>> partition(String s) {
        dfs(s, 0, 0);
        return ans;
    }

    public void dfs(String s, int i, int last) {
        if (i == s.length()) {	// 要选的字符已经选完了
            ans.add(new ArrayList(t));
            return;
        }
        if (i + 1 < s.length()) dfs(s, i + 1, last);	// 不选当前字符
        if (check(s, last, i)) {	// 如果当前字符可以被选择
            t.add(s.substring(last, i + 1));
            dfs(s, i + 1, i + 1);	// 由于当前字符要被选择了，所以下一个回文子串从i + 1开始
            t.remove(t.size() - 1);
        }
    }

    public boolean check(String s, int l, int r) {
        while (l < r) {
            if (s.charAt(l++) != s.charAt(r--)) return false;
        }
        return true;
    }
}

补充：怎么判断回文串

双指针

https://leetcode.cn/problems/find-first-palindromic-string-in-the-array/
两边各设置一个指针，分别为 l 和 r，逐步移动并比较是否相同。

或者叫 中心拓展法 ，从中间开始逐步向两边移动并比较。

class Solution {
public:
    string firstPalindrome(vector<string>& words) {
        // 判断字符串是否回文
        auto isPalindrome = [](const string& word) -> bool {
            int n = word.size();
            int l = 0, r = n - 1;
            while (l < r) {
                if (word[l] != word[r]) {
                    return false;
                }
                ++l;
                --r;
            }
            return true;
        };
        
        // 顺序遍历字符串数组，如果遇到回文字符串则返回，未遇到则返回空字符串
        for (const string& word: words) {
            if (isPalindrome(word)) {
                return word;
            }
        }
        return "";
    }
};

dp提前处理

https://leetcode.cn/problems/palindromic-substrings/

class Solution {
    public int countSubstrings(String s) {
        int n = s.length(), ans = 0;
        boolean[][] dp = new boolean[n][n];
        for (int i = n - 1; i >= 0; --i) {
            for (int j = i; j < n; ++j) {
                dp[i][j] = s.charAt(i) == s.charAt(j);
                if (j > i + 1) dp[i][j] &= dp[i + 1][j - 1];
                if (dp[i][j]) ++ans;
            }
        }
        return ans;
    }
}