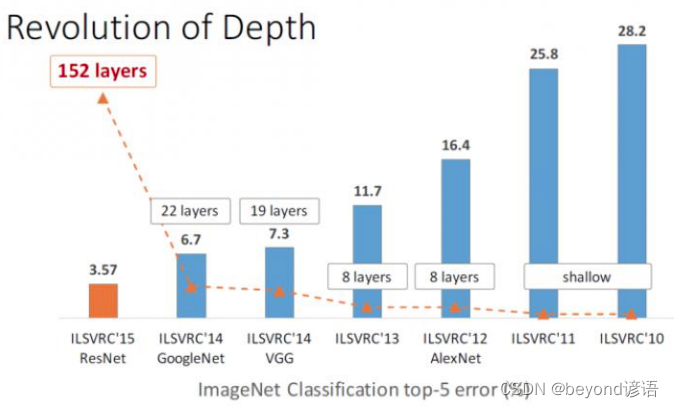
vins中的光流法
说到光流法,首先介绍其假设条件:
1.亮度恒定,就是同一点随着时间的变化,其亮度不会发生改变。这是基本光流法的假定(所有光流法变种都必须满足),用于得到光流法基本方程。就是在一阶Taylor展开以后求解变化量。
2.小运动,这个也必须满足,就是时间的变化不会引起位置的剧烈变化,这样灰度才能对位置求偏导(换句话说,小运动情况下我们才能用前后帧之间单位位置变化引起的灰度变化去近似灰度对位置的偏导数),这也是光流法不可或缺的假定。当然快速运动的情况也有用光流法的算法,这时候上一个图像金字塔基本就可以解决快速运动的问题了。
3.空间一致,一个场景上邻近的点投影到图像上也是邻近点,且邻近点速度一致。这是Lucas-Kanade光流法特有的假定,因为光流法基本方程约束只有一个,而要求x,y方向的速度,有两个未知变量。我们假定特征点邻域内做相似运动,就可以连立n多个方程求取x,y方向的速度(n为特征点邻域总点数,包括该特征点)
以上就是光流法的假设条件,一般就是灰度不变性、小运动和空间一致。
算法原理:

编辑切换为居中
添加图片注释,不超过 140 字(可选)
上面首先进行了一阶Taylor展开,然后前后灰度不变,那么I(x+dx,y+dy,t+dt) = I(x,y,t),那么Taylor展开的一阶项等于0,再对一阶项除以dt,就得到了上面的公式。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
基于上面第三条假设,空间一致性,得到了n个方程,然后最小二乘求解一下即可得到u和v,这里的uv就是像素坐标的变化量,也即是速度。可以看到光流法是来估计物体运动的(估计的是物体运动的速度,根据速度再计算相对应的特征点)。
算法改进:
LK算法的约束条件即:小速度,亮度不变以及区域一致性都是较强的假设,并不很容易得到满足。如当物体运动速度较快时,假设不成立,那么后续的假设就会有较大的偏差,使得最终求出的光流值有较大的误差。
Jean-Yves Bouguet提出一种基于金字塔分层,针对仿射变换的改进Lucas-Kanade算法
构建图像金字塔可以解决大运动目标跟踪,也可以一定程度上解决孔径问题(相同大小的窗口能覆盖大尺度图片上尽量多的角点,而这些角点无法在原始图片上被覆盖)
主要思想
考虑物体的运动速度较大时,算法会出现较大的误差。那么就希望能减少图像中物体的运动速度。一个直观的方法就是,缩小图像的尺寸。假设当图像为400×400时,物体速度为[16 16],那么图像缩小为200×200时,速度变为[8,8]。缩小为100*100时,速度减少到[4,4]。
所以光流可以通过生成 原图像的金字塔图像,逐层求解,不断精确来求得上层金字塔(低分辨率)中的一个像素可以代表下层的两个
对于Lucas-Kanade改进算法来说,主要的步骤有三步:建立金字塔,基于金字塔跟踪,迭代过程。
这里是对LK光流法的改进,在vins里面也有到了这个思想,同时这里的基于图像金字塔的光流法在vins中是直接调用的opencv接口,非常的方便。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
首先是建立金字塔的过程,通常我们把原始图片放在金字塔的最下面,称为第0层,然后依次往上对图片进行降采样,也即使用上面的公式来计算灰度值。在vins中应该是使用的4层金字塔。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
下面这个做法也很好理解,梳理一下基于图像金字塔的光流法:
首先是建立图像金字塔,从第0层放入原始图像开始,然后依次向上建立金字塔。然后光流法开始,从金字塔的最上面开始跟踪,因为上面分辨率低,光流法能够很轻松地跟踪,并解算当前金字塔层的运动情况。然后当前层光流法结束以后,会得到一个解,将这个解放到下一层,作为初值,然后继续进行光流法。那么下一层基于这个初值也会得到一个解,就这样进行迭代,直到达到金字塔的最底层,也即第0层,就是原始分辨率的那张图片,此时光流法就会给出一个速度值,这个值是比较可靠的(相比对原始图片直接使用光流法来说)。以上过程便是基于图像金字塔的一个流程,可以简单记作:先从图像金字塔的第0层开始建立,依次向上,然后再从图像金字塔的最顶层开始往下,依次光流跟踪。这便是基于图像金字塔的光流法的整个流程。