目录

✿LeetCode110.平衡二叉树❀

✿LeetCode257.二叉树的所有路径❀

 ✿LeetCode404.左叶子之和❀

---

✿LeetCode110.平衡二叉树❀

链接：110.平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

 

 分别求出左右子树的高度，然后看相差是否大于1，代码如下：

public boolean isBalanced(TreeNode root) { 
        if(getHeight(root)==-1){
            return false;
        }
        return true;
    }
    public int getHeight(TreeNode root){
        if(root==null){
            return 0;
        }
        int leftH=getHeight(root.left);
        if(leftH==-1){
            return -1;
        }
        int rightH=getHeight(root.right);
        if(rightH==-1){
            return -1;
        }
        if(Math.abs(leftH-rightH)>1){
            return -1;
        }else{
            return 1+Math.max(leftH,rightH);
        }
    }

✿LeetCode257.二叉树的所有路径❀

链接：257.二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

 

这道题是求二叉树的所有路径，我用了回溯算法，代码如下： 

List<String> result;
    List<Integer> path;
    public List<String> binaryTreePaths(TreeNode root) {
        result=new ArrayList<>();
        path=new ArrayList<>();
        if(root==null){
            return result;
        }
        traversal(root);
        return result;

    }
    public void traversal(TreeNode root){
        path.add(root.val);    //中
        if(root.left==null && root.right==null){
            String str="";
            for(int i=0;i<path.size()-1;i++){
                str+=path.get(i).toString();
                str+="->";
            }
            str+=path.get(path.size()-1).toString();
            result.add(str);
        }
        if(root.left!=null){
            traversal(root.left);   //左
            path.remove(path.size()-1);  //回溯
        }
        if(root.right!=null){
            traversal(root.right);  //右
            path.remove(path.size()-1);   //回溯
        }
        
    }

 ✿LeetCode404.左叶子之和❀

链接：404.左叶子之和

给定二叉树的根节点 root ，返回所有左叶子之和。

 

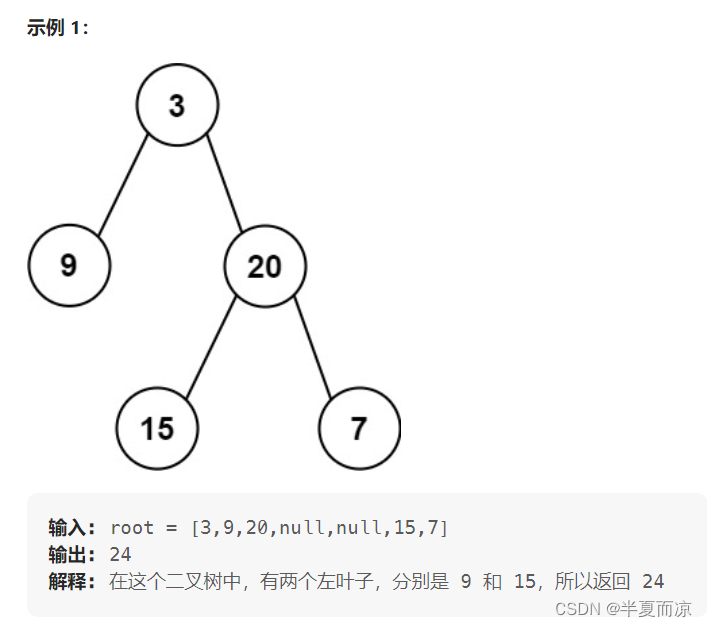
这道题关键在于，什么是左叶子，左叶子就是左孩子的左右孩子都为空，即可写出如下代码： 

public int sumOfLeftLeaves(TreeNode root) {
        if(root==null){
            return 0;
        }
        int leftsum=sumOfLeftLeaves(root.left);
        if(root.left!=null && root.left.left==null && root.left.right==null){
            leftsum=root.left.val;
        }
        int rightsum=sumOfLeftLeaves(root.right);
        int sum=leftsum+rightsum;
        return sum;
    }