概述
数据库设计是一项十分复杂的操作,首先需要理清数据之间的关系,绘制ER图,接着根据ER图设计Relation Schema,最后添加字段属性和索引生成数据表。一个好的ER图是一个数据库的基础。
数据库设计的好坏中最重要的一项指标就是重复率,而降重的常用方法是分解(Decomposition )。
Decomposition
并不是所有的分解都是有效的,分解之后的数据可能会无法组成原来的数据表,此时我们称为有损分解(Lossy decomposition )。
当一个R被分解为R1, R2之后,如果R1∩R2中的字段可以构成R1或R2的Super Key,则该分解是无损的。
这里需要注意的一点是,有损分解并不是指数据会变少恰恰相反,有损分解之后的数据表再重新组合后会引入更多的数据,但这些数据都是错误的信息。有损实际上指的是信息的丢失。
FD(Functional Dependency)
当已知一个(或一组)属性就可以确定另一个(或一组)属性的数据时,我们就称这两个属性之间存在关系依赖(functional dependency),简称FD。FD用符号→ 表示,A → B 表示A决定B,也称B依赖于A。很容易想到一个表中的所有数据都对主键存在关系依赖。关系依赖也就是存在A到B的函数关系,即多个A中的数据可以映射到一个B,但一个A中的数据不能映射到多个B。
A和B均可以是一个或一组属性,当A为一组属性时,我们称其为复杂依赖。
这里我们需要明确几个概念,Key表示一个可以唯一确定一个数据的最小的一组属性,说人话就是根据Key就可以唯一确定一行。其中一个Key在数据表中会被选为主键Primary Key,而其他的Key称为候补键Candidate Key。Super Key是Key的母集,其定义是可以唯一确定一个数据的一组属性,不需要最小,也就是说每行数据本身就是自己的Super Key,而一组数据如果想要成为Super Key,其中至少要包含一个Key。
依赖图示例:
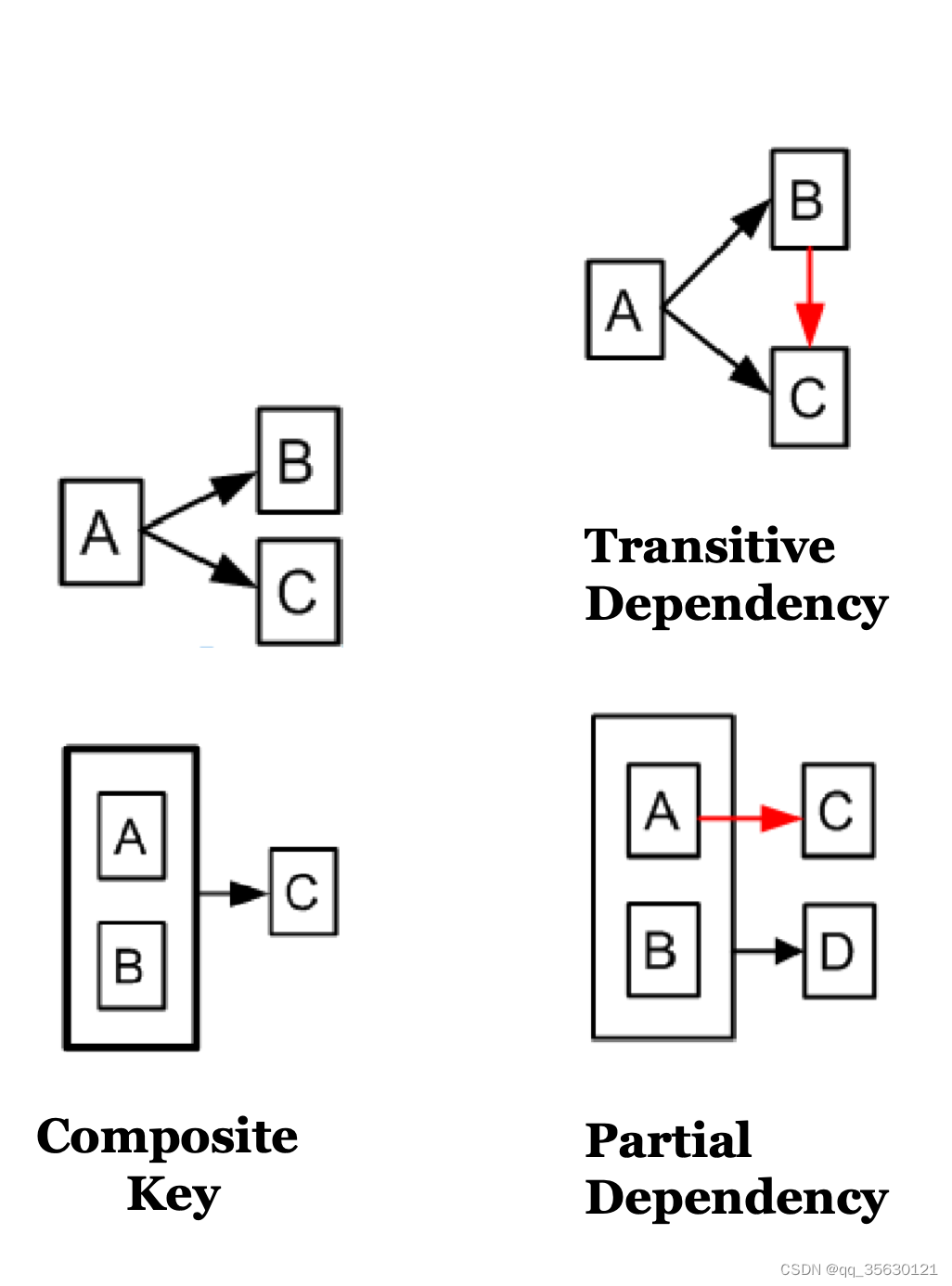
FD定律
- 反射性(reflexivity):如果B是A的子集,那么有 A → B
- 增强性(augmentation):如果A → B,那么AC → BC
- 传递性(transitivity):如果A → B,B → C,那么有A → C
- 可加性(additivity):如果A → B,且A → C,那么有A → BC
- 投射性(projectivity):如果A → BC,那么有A → B, A → C
- 伪传递性(pseudo-transitivity):如果A → B,且BC → D,那么AC → D
FD闭包与属性闭包
当我们已知一个R中的部分FD时,可以通过上述FD定律推演出许许多多额外的FD,而一个包含所有原始FD和推演FD的FD集合就称为FD闭包,用符号F+来表示。
随着F+的大小会随着原始FD数量而指数型增加,因此一般不使用,也没有什么实际意义。
与FD闭包类似的还有属性闭包,属性闭包的概念是使用原始属性和FD可以决定的最多属性的集合,通常用符号X+表示。可以使用以下方法来获得属性的闭包:
result := a;
while (changes to result) do
for each b → c in F do
begin
if b ∈ result
then result := result ∪ c
end
上述方法有些过于公式化,简单来说就是先将原始属性添加到闭包中,随后通过FD,将所有能推导出的属性也添加到闭包中。
当一组属性的闭包包含R中的所有属性时,该组属性就是R的一个Super Key。
获取Candidate Key
通过属性闭包可以获取一个R中的所有Candidate Key,具体方法是:
- 尝试移除一个R中的属性,得到一个子集X,如果X的闭包等于R,则X为Super Key。
- 尝试移除X中的一个属性,使得到的子集的闭包仍为R,并令新子集为X。
- 如果没有任何属性可以移除,则X为一个Candidate Key。
- 重复123步,知道获取所有的Candidate Key,即遍历所有可能性。
最小FD集
由于FD之间有着丰富的推演关系,因此一个相同的FD关系可能会被多个FD集所表示。这里的相同在学术上的意思是两个FD集的F+相同。
但在实际应用中,这种不确定性并不会带来什么好处,而且过多的FD反而会影响我们发现主要关系,因此实际应用中我们更希望一种FD关系有一个固定的、简约的表示,这就是最小FD集的由来。
最小FD集有三个特点:所有FD关系右边必须是单个属性,左边的每个属性都不可舍弃,每个FD关系都不可舍弃,也就是不存在可以被其他FD推导出的FD。
满足以上三个条件的FD集就称为最小FD集,将一个FD集转换为最小FD集用的是与上述特点对应的三个步骤:
- 拆分所有FD关系的右边,将多个属性拆分为多个单属性的FD,例如AB → CD需要拆分为AB → C, AB → D
- 遍历所有FD的左边的,删去非必须项,例如,同时存在 A → B, AB → C,那么AB → C中的B是非必须的,因此应该简化为A → B, A → C,或者同时存在A → C, AB → C,那么AB → C中的B可以删去。
- 删除所有可以被推导出的FD关系,例如,同时存在 A → B, B → C, A → C,那么A → C是可以被A → B, B → C推导出的,需要删除
第一步比较简单,没什么可说的。第二步需要逐个计算左边剔除一个字段之后剩余字段的闭包,如果闭包中包含右边字段,则该字段可以被删除,否则不能删除。第三步只能慢慢看了。
范式
第一范式(1NF):数据表中的每个字段中不能存储多个值。
第二范式(2NF):在满足第一范式的基础上,一个数据表中的非主属性必须完全依赖于一个key,不能部分依赖于一个key。
第三范式(3NF):在满足第二范式的基础上,不能存在非Key属性之间的依赖关系,即其他属性不能依赖非主键。从FD的角度来说,第三范式不允许表中出现通过非主属性实现的传递关系。
Boyce-Codd 范式(BCNF):在满足第三范式的基础上,一个数据表中的被依赖的一组属性必须是Super Key,不能依赖于一组非Super Key的属性。
简单来说,数据库三范式就是为了设计一个具有原子字段(1NF)的,且数据表中除完整的主键外没有任何依赖关系(2NF,3NF)的数据库。
第一范式
一个人可以有多个手机号,假如我们现在想要创建一个数据库存储一个人的id,姓名和手机号。
如果创建数据表为person(pid, name, phone),其中phone字段存储格式为’phone1,phone2,phone3…',那么该字段就是不符合第一范式的,因为phone字段中保存了多个手机号。
解决办法
可以看出,phone相当于person的一个Multivalued Attribute,相当于一个一对多关系,需要创建一个新的数据表person_phone(pid, phone)
第二范式
第一范式是实现第二范式的前提。在第二范式中,一个R中可能存在多个Candidate Key。如果一个属性属于任何一个Candidate Key,就称为主属性,否则称为非主属性。
现在网上许多人将第二范式定义为主键完全依赖,这是不准确的,因为第二范式并没有规定一个R中不能有多个Candidate Key。对于非主键的Candidate Key,同样需要相关的非主属性完全依赖。
而主键完全依赖其实是第二范式与第三范式结合的结果,这就话也是不对的。
解决办法
如果一个R中存在不满足第二范式的属性,那么需要将该非主属性和其部分依赖的Key中的部分属性从R中提取出,创建一个新表。
例如,假如有一个数据表student_course(sid, cid, s_name, c_name, grade),其中sid, cid共同构成主键。但是很容易发现,s_name只依赖于sid,c_name只依赖于cid,即F = {sid → s_name, cid → c_name, sid cid → grade}。两个字段都只部分依赖于主键。
此时正确的做法应该是将sid与s_name提取出单独成表,cid和c_name提取出单独成表,最后得到RC为student_course(sid, cid, grade), student(sid, s_name), course(cid, c_name)。
第三范式
第二范式是实现第三范式的前提。在第三范式中,不能存在非主属性之间的依赖。因为从理论上来说,一个属性如果被依赖,那么他就应该作为key,如果在当前表中不能称为key,就应该为其创建新表。
也就是说,只要一个FD的被依赖属性是完整的活部分Key,就可以满足第三范式,这同样会有一定的风险。
解决办法
如果一个R中存在不满足第三范式的字段,则需要将依赖于非主属性的字段从表中提取出,并以依赖的非主属性字段为主键创立新表。
例如,有一个表student_course(sid, cid, grade, level),grade为课程分数,level为课程评级,很容易发现该表的FD = {sid cid → grade, grade → level}。存在非主属性之间的依赖关系grade → level。
此时应该将level属性提取出,与grade一起创建新表,最终得到两个数据表student_course(sid, cid, grade), grade_level(grade, level)
BCNF
第三范式是实现BCNF的前提。在BCNF中,被依赖的属性必须是Super Key,不能是一个Key的部分字段。从FD的角度来说,如果存在依赖关系 A → B,那么A必须是Super Key。
123范式的实现不会导致任何信息的丢失,而BCNF并不是任何时候都适用的,在某些情况下可能会导致依赖保持(dependency preserving)信息的丢失,在实现时需要注意。
解决办法
如果一个R中存在不满足BCNF的字段,则需要将依赖字段从表中提取出,并将其依赖的字段作为主键构建新表。
例如,有一个表 booking(title, theater, city),其FD = {theater → city, title city → theater}。可以得出其Candidate Key为{title, city}和{title, theater}。而其中FD theater → city,由于theater不是super key,不满足BCNF。
需要将city从booking表中提取出,与theater构成新表theater_city(theater, city) FD = {theater → city},原表剩下booking(title, theater),此时两表均满足BCNF。
即,找出表中的所有FD,检查所有FD中的被依赖字段是否为Super Key,如果不是则以被依赖字段作为主键,依赖字段作为其他属性创建新表,并在原表中删除被依赖字段
例子:
Relation: R(ABCD) FD: B → C, D → A,Only Key:BD。
- 对于FD: B → C,由于B不是Super Key,原关系分解为R1(BC)和R2(ABD)
- 对于FD: D → A,由于D不是Super Key,R2分解为R3(DA)和R4(BD)
依赖保留(Dependency Preservation)
在上面的分析中,我们一直在讨论降重的方法,但实际上除了降重之外,依赖保留也是要考虑的。幸运的是,1NF,2NF和3NF在可以降重的同时都是支持依赖保留的,只有BCNF有时候会对依赖关系就行一些舍弃。
这里我们要了解一个新概念,即F的投影。在上述分析中,我们已知降重需要用到分解,而分解不只是数据表的分解,DF也随之分解并继承到了对应的新表上。而所谓的F的投影指的就是新表的DF关系以及旧表保留的DF关系,用符号Fi表示,其中i为对应数据表的下标。
例如我们有一个数据表R(A, B, C),其F = {A → B, B → C}。很明显其不满足第三范式,我们需要将其分解为R1(A, B), R2(B, C),两个新表的DF分别为F1 = {A → B}, F2 = {B → C}。F1和F2就称为F的投影。
而依赖保留指的就是在一个数据表被分解之后,F的所有投影可重新组合成F。这里需要注意的是,并不是要求(F1∪F2∪F3…) = F,而是(F1∪F2∪F3…)+ = F+。但在实际的计算中我们不可能去比较二者的闭包,只需要使用DF之间的关系特性尝试推导出完整的F即可。
范式总结
在理想情况下,一个数据表中只存在一种FD,即F = {ABC… → abc…},其中ABC…为主键,abc…为主键外的其他属性,即非主属性。
当存在类似于FD = {ABC… → abc…, A → a, B → b }的关系时,说明该表不满足第二范式,需要拆表。分别将属性a和属性b提取出并与对应的依赖属性A和B成表(A, a) (B, b)。
而当存在类似于FD = {ABCD… → abcd…, b → cd}的关系时,说明该表不满足第三范式,需要拆表。将属性cd提取出,并与其依赖的b成立新表(b, c, d)。
3NF会完全保留DF关系,但可能存在重复;而BCNF会完全消除重复,但可能发生关系丢失。在实际使用中,需要根据情况选择使用3NF还是BCNF。
更高的规范化标准同时意味着更多的数据表,虽然可以节省存储空间、避免更新错误,但更多的数据表意味着查询时需要join更多的表,这回影响查询速度。在实际应用中,我们通常还要根据业务需求,对一些需要经常查询的字段进行反规范化处理。
事务
事务是一个流程,表现在代码上就是一组代码。
四个特点ACID
原子性(Atomicity):事务不可分割,一个事务内的所有代码要么全部成功,要么全部失败
一致性(Consistency):这个比较抽象,对应的要求大概是事务不对外展示中间态,即所有事务读取到的都是其他事务开始前和结束后的数据,不会读取到中间数据
隔离性(Isolation):事务之间彼此隔离,互不影响。
持久性(Durability):事务结束后对数据库的影响持久存在,即使设备发生故障。
冲突可序列化(Conflict Serializability)
在实际应用中,为了提高效率,事务一般都是并发的。而并发就要避免冲突,因此需要良好的事务调度。
理想的无冲突情况就是事务串行,当一种调度的结果在冲突层面上与串行是一致的时,我们就称这种调度方式是冲突可序列化的。
实际的数据库系统会通过一些额外的方法(例如锁)来保证所有的调度都是冲突可序列化的。而如果我们想判断一个已知的调度是否是冲突可序列化,可以使用precedence graph。
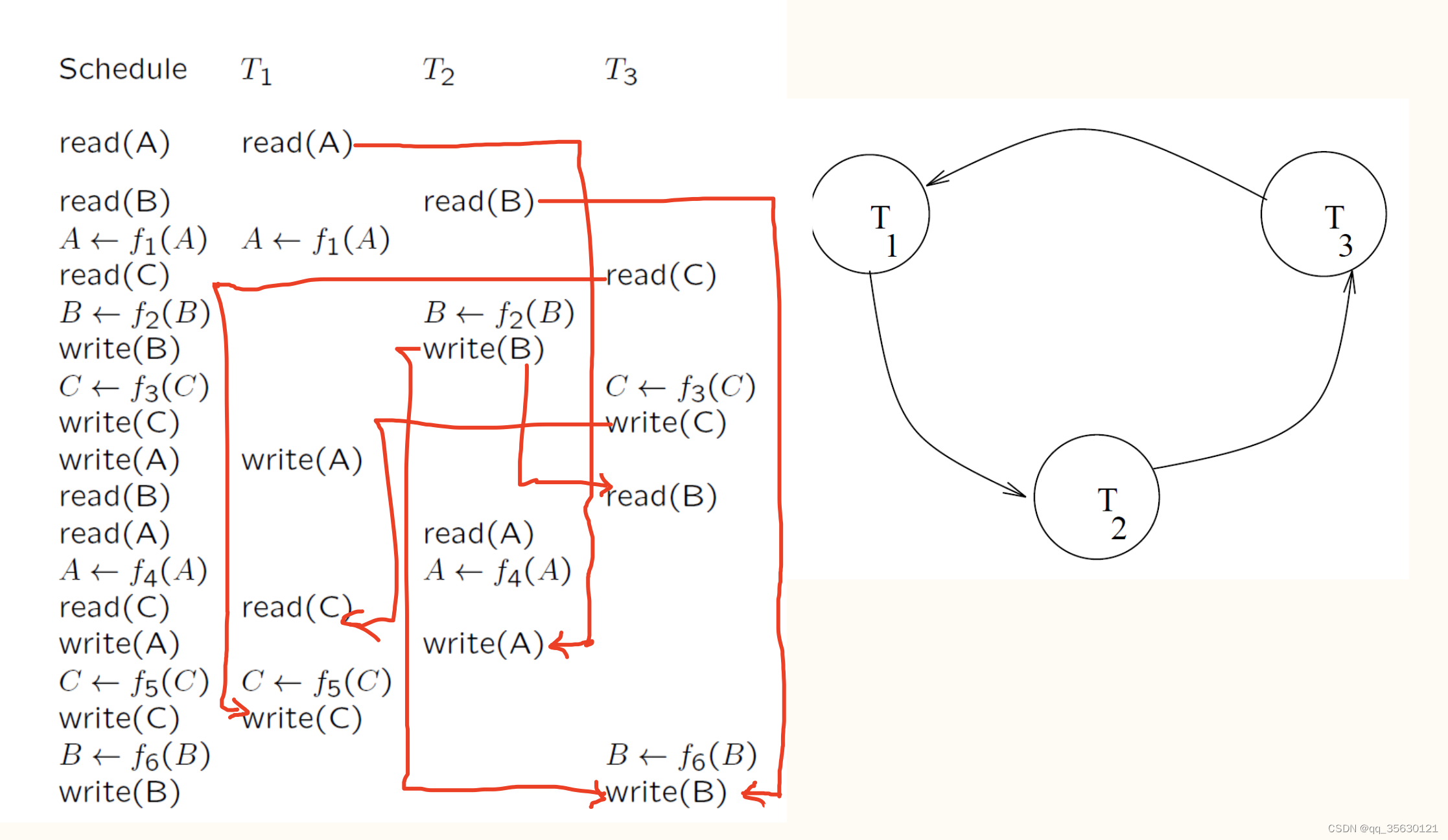
Precedence Graph
为了绘制precedence graph,我们首先需要知道对应的调度(schedule)。在调度中,我们只关心数据的读操作和写操作。以下三种调度序列会导致冲突:
- Read → Write
- Write → Read
- Write → Write
在precedence graph中,事务表示为一个点,数据流表示为一个带箭头的弧线,图中只绘制可能发生冲突的数据流。
当一个precedence graph中存在环时,则说明该调度不是冲突可序列化的,也就是存在风险。反之,如果图中没有环状结构,则说明该调度是冲突可序列化的。
两个事务即使有多个冲突也只需要绘制一条曲线。
锁
锁是保证序列化的最常用工具。一个锁会与一个对象绑定,在数据库中就是与一个表或者一行绑定。在访问(R&W)数据时需要先获取其对应的锁。
锁按照访问权限可以分为读锁(Write Lock)和写锁(Read Lock),也叫共享锁(Share Lock)和排它锁(Exclusive Lock)。
一个共享锁在加锁之后允许其他事务的读操作,但会拒绝写操作,也就是写操作需要等读操作进行完毕并且释放锁之后。
而排它锁在加锁之后会拒绝所有的读写操作。
由于事务的原子性,一个事务对一个锁只能有一个获取操作。如果其对一个数据的全部操作均为读,则获取其读锁,如果至少有一个操作是写,则获取其写锁。获取的锁会在事务对数据的所有操作均结束之后才会被释放。
通过对读写操作进行加锁可以保证事务调度的可序列化,为了保证调度的可序列化,需要使用2PL(Two Phase Locking)规则,即一个事务的生命周期需要分为两个阶段,在第一阶段只能获取锁不能释放锁,在第二阶段只能释放锁不能获取锁。也就是说锁不能在数据操作完就释放,需要等待事务结束时统一释放。
死锁
由于事务会保持锁直到结束,那么很容易想到一种情况,假如事务T1,T2都需要操作A,B数据,T1首先获取了A的锁,T2获取了B的锁,在T1、T2分别处理完了A和B之后需要获取B和A的锁。此时T1和T2会一直互相等待下去,这种情况称为死锁。
死锁在事务调度中不可避免,但需要有对应的处理方式。常用的方式是通过绘制等待关系图(Wait-for Graph)来判断是否存在死锁。当等待关系图中存在环时代表存在死锁。
当死锁发生后需要强制中断其中的一个事务,即打破环状结构。
TSO(Timestamp Ordering)
除了使用锁以外,还有着许多无锁的调度规则,TSO就是其中之一。其原理是在每个事务开始时都为其打上一个时间戳,在操作数据时同样需要获取锁。与加锁方式不同的地方在于,当发生R → W, W → R, W → W这样的情况时,新的想要获取锁的事务不会进行等待,而是由数据库管理系统直接restart时间戳较大(即比较新)的事务。在restart时,事务的时间戳保持不变,防止同一个事务一直被restart。
TSO的优点在于不会引起死锁,管理简单,但其资源利用率相比加锁方式较低,还会引起较多的回滚。
索引
索引可以分为聚集性索引和非聚集性索引,其中聚集性索引只能有一个,数据会按照聚集性索引进行排列,在数据库中聚集性索引即是主键索引。
按照是否直接存储数据地址,可以分为内层索引和外层索引。其中内层索引存储的是数据地址,而外层索引存储的是内层索引的地址。外层索引的作用是降低查询时间,因为实际数据通常都很大。假设有100万条数据,如果只有一层索引那在查询时需要遍历100万条数据,如果我们外接一层索引,索引长度为1000,同时设计1000个内层索引,长度同样为1000,那么在查询时只需遍历2000条数据,可以大大缩小查询时间。
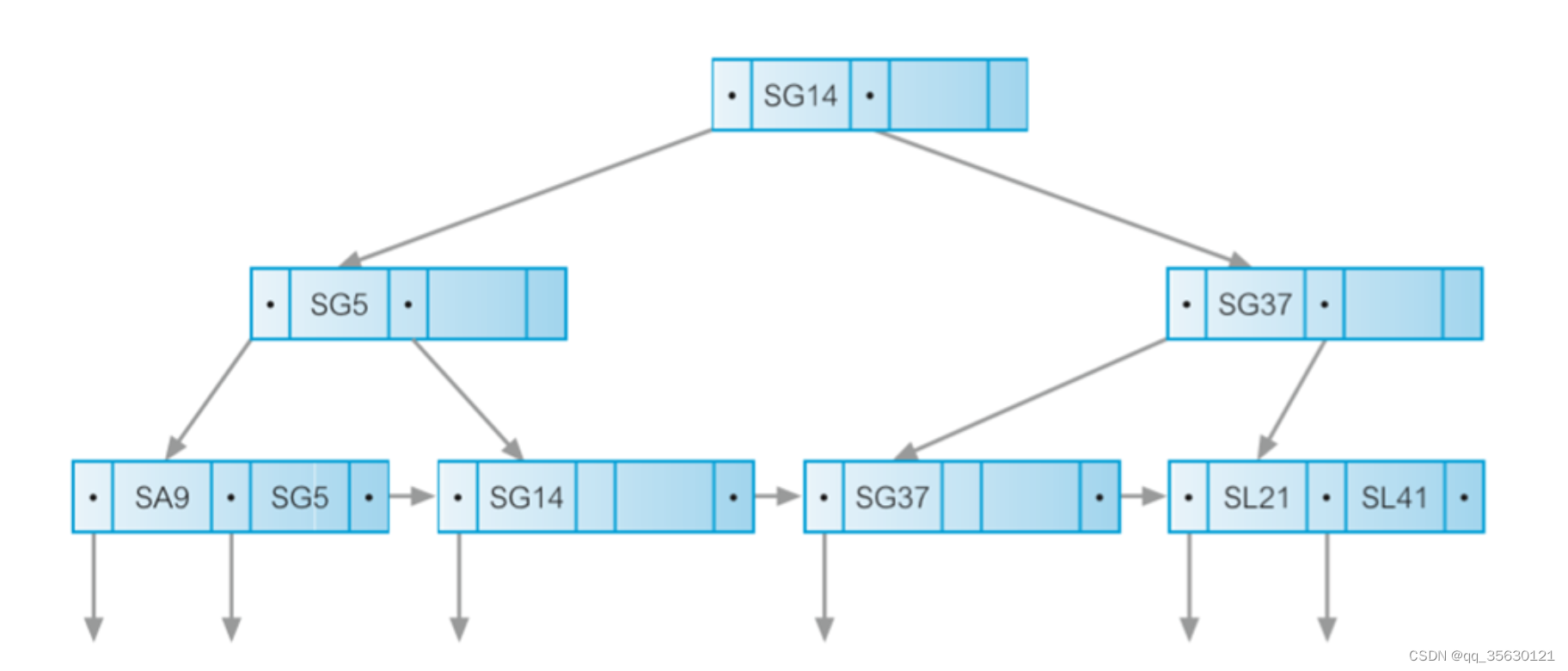
外层索引可以有多层,视具体情况而定。B+树就是一个典型的多层索引。
索引底层结构可以由B+树和哈希表实现,B+树的优势在于可以支持范围查找,因此现在索引默认格式为B+树。
B+树
B+树的一个节点是由交替排列的key和指针p组成的,其中root节点和中间节点存储的是指向子节点的指针,而叶子节点存储的是指向数据地址的指针。同时每个叶子节点还会保存相邻叶子节点的指针,以实现范围查询。
在范围查询时,首先查找到左边界的位置,随后在叶子节点中从左向右遍历取出所有数据,知道叶子节点中的key值大于右边界为止。
每一层的容量是由key的长度和读取磁盘时每一页的大小所决定的。由于索引的作用就是要加快读取速度,因此索引本身不能加载过慢,在每次取出数据时必须取出整个节点。因此每一层的节点容量大致为 页大小 / (key.length + pointer.length)。
在存储字符串类型的key时,由于key的长度是变化的,因此无法确定节点的容量。一个有效的解决办法是每层节点的key只保存固定长度的字符串前缀,对于前缀相同的字符串则在后续节点进行区分。
在查询数据时,从root节点出发,从左向右遍历每一个key值,如果查询的key大于当前key,则继续遍历,否则根据当前key左边的指针访问下一级节点重复该过程,直到获取到数据地址。
在插入数据时,数据首先会被插入对应位置的叶子节点,如果叶子节点容量足够,则完成插入。如果叶子节点位置不够,则需要将叶子节点从中间进行分裂,并将中间的key提取到上一层,并插入上一层的对应位置。如果上一层的位置足够则结束插入,如果位置不够则继续分裂。
在删除数据时,同样是要先删除叶子节点对应位置的数据。在删除完成后首先会尝试和叶子节点左边的节点进行合并,如果左边没有叶子节点则会尝试与右边的叶子节点合并。在合并完成后,如果节点没有超过容量,则删除结束,如果超过了容量则需要按照插入的方式进行分裂。
当key为多个字段时,会按照从左到右的顺序根据多个字段构建新的key,因此使用完整的索引或单独使用左边的索引可以生效,而单独使用右边的索引不会生效。
哈希表
基础知识,就不赘述了。不常用的原因就是不支持范围查找。
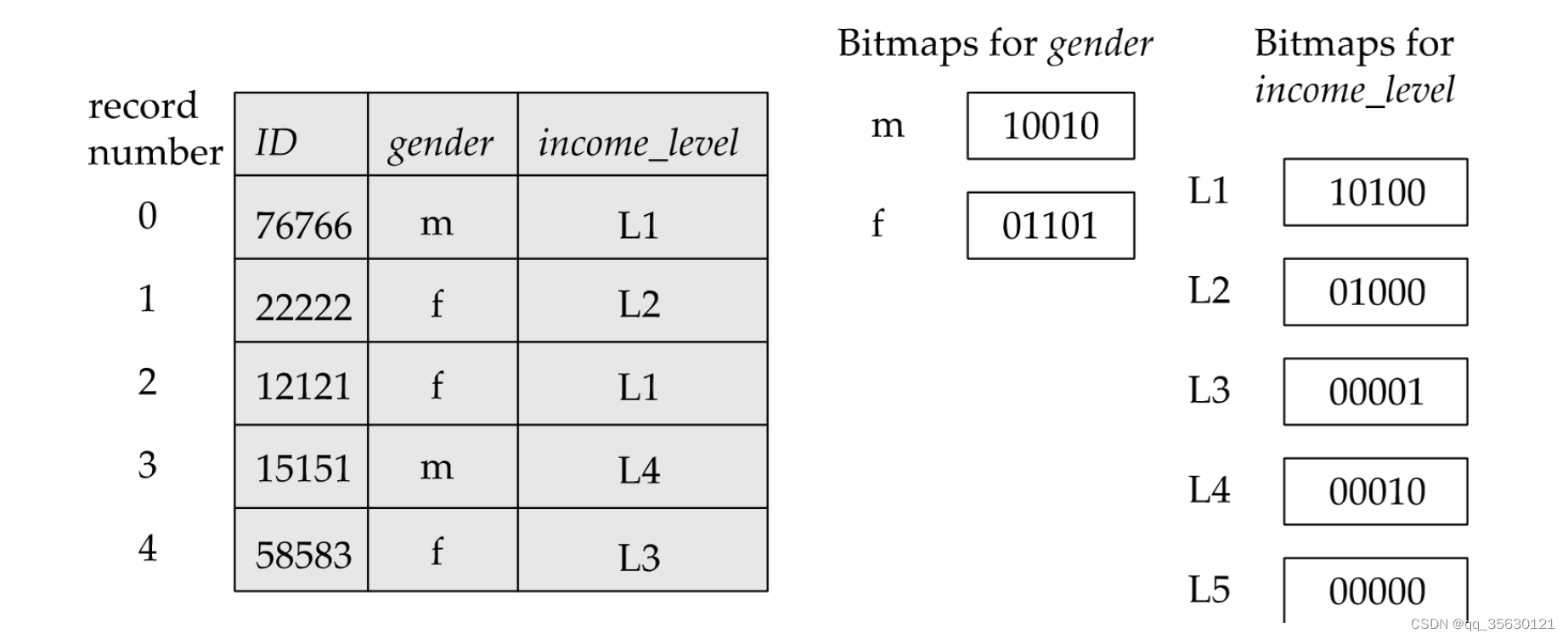
Bitmap
除B+树和哈希表之外,Bitmap也是一类索引结构。Bitmap适用于key值较少,重复的key较多的情况,例如性别,颜色等等。左边为key值,右边是与数据长度相等的01序列,其中1代表对应位置的数据符合索引。
Bitmap可以直接使用右边的数据实现与和并的操作。
![分布式文件存储系统FastDFS[2]-上传和下载文件工具类](https://img-blog.csdnimg.cn/00771231adde482c92c58e6c0478cb35.png)

![[附源码]计算机毕业设计农产品销售网站Springboot程序](https://img-blog.csdnimg.cn/f40e308388db44c68df7e7245d2472ce.png)





![[附源码]Python计算机毕业设计Django校刊投稿系统](https://img-blog.csdnimg.cn/b1cc6ac70b954d0885ea6ad540ef84d4.png)

![[附源码]计算机毕业设计青栞系统Springboot程序](https://img-blog.csdnimg.cn/b953bb0bf76942879006a02b1075c47e.png)
![[附源码]JAVA毕业设计沙县小吃点餐系统(系统+LW)](https://img-blog.csdnimg.cn/7132c19018274e6fa104c8d6aab2f04c.png)


