本文中我在R中构造一个简单的M / M / 1队列的离散事件模拟 。最近我们被客户要求撰写关于随机服务的研究报告，包括一些图形和统计输出。

模拟变量

像往常一样，我们从模拟及其检测所需的变量 开始。

 
t.end <- 10^5 # 模拟的持续时间
t.clock <- 0 # 模拟时间
Ta <- 1.3333 # 抵达间隔期
Ts <- 1.0000 # 服务期
t1 <- 0 # 下一次到达的时间
t2 <- t.end # 下一次出发的时间
tn <- t.clock # 最后事件时间的临时变量
tb <- 0 # 最后一次繁忙时间开始的临时变量
n <- 0 # 系统中的数量
s <- 0 # 累积数量-时间乘积
b <- 0 # 总忙碌时间
c <- 0 # 总完成数
qc <- 0 # 绘制瞬时q大小
tc <- 0 # 绘制时间延迟图
plotSamples <- 100
set.seed(1) 

接下来，我们需要编写R代码以对进入队列和从队列离开进行实际的M / M / 1模拟。

仿真循环
 

while (t.clock < t.end) {
    if(t1 < t2) { # 到达事件
        t.clock <- t1
        s <- s + n * (t.clock - tn) # 队列中的delta时间加权数
     
...

        else { 
            t2 <- t.end
            b <- b + t.clock - tb
        }
    }   
}

检测指标

在这里，我们 检测数据以形成一些众所周知的性能指标。 

队列长度

这是瞬时队列长度- 平均负载数据的曲线图。这就是排队波动的样子。 

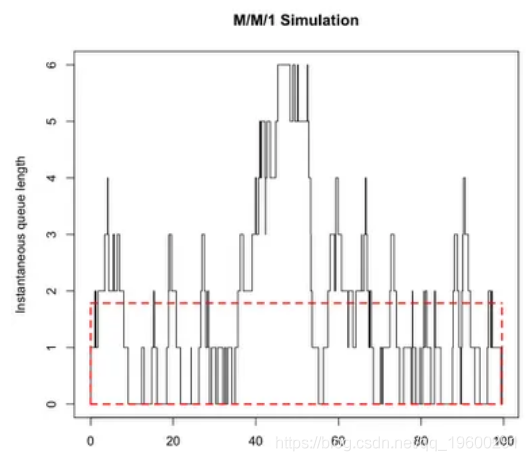
显示为红色虚线的框具有与阶梯曲线下方相同的面积。 

PDQ模型

为了进行分析比较，我们还使用 PDQ-R模型。

是的，这几行代码与上面带工具的仿真代码等效，并且可以保证处于稳定状态。即使在R中运行PDQ本质上也是瞬时的。模拟将花费更长的时间， 

结果

最后，我们可以将模拟的M / M / 1队列与相应的PDQ结果进行比较。像往常一样，最好将它们分解为输入和输出。

1. 输入：

   Tsim：1.00e + 05 
   Ta：1.3333，Ts：1.0000＃次
   Ar：0.7500，Sr：1.0000＃
   

2. 输出：

   Usim：0.7477，Updq：0.75 
   Xsim：0.7495，Xpdq：0.75 
   Rsim：4.0316，Rpdq：4.00 
   Qsim：3.0219，Qpdq：3.00

 我们可以得出结论，仿真在指定的10 5个时间步长内达到了稳态。