一、二叉树

与链表类似，二叉树的基本单元是节点，每个节点包含一个「值」和两个「指针」。

在二叉树中，除叶节点外，其他所有节点都包含子节点和非空子树。

一些术语：

• 「根节点 Root Node」：位于二叉树顶层的节点，没有父节点；
• 「叶节点 Leaf Node」：没有子节点的节点，其两个指针均指向 None ；
• 节点的「层 Level」：从顶至底递增，根节点所在层为 1 ；
• 节点的「度 Degree」：节点的子节点的数量。在二叉树中，度的范围是 0, 1, 2 ；
• 「边 Edge」：连接两个节点的线段，即节点指针；
• 二叉树的「高度」：从根节点到最远叶节点所经过的边的数量；
• 节点的「深度 Depth」 ：从根节点到该节点所经过的边的数量；
• 节点的「高度 Height」：从最远叶节点到该节点所经过的边的数量；

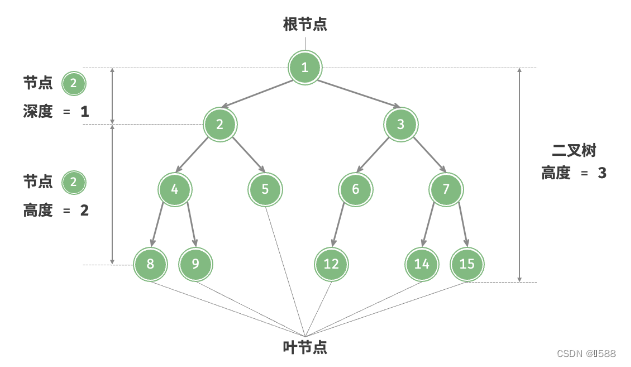
可以看出来二叉树的高度等于层数-1（因为根节点是层1）

知识点1：常见二叉树类型：

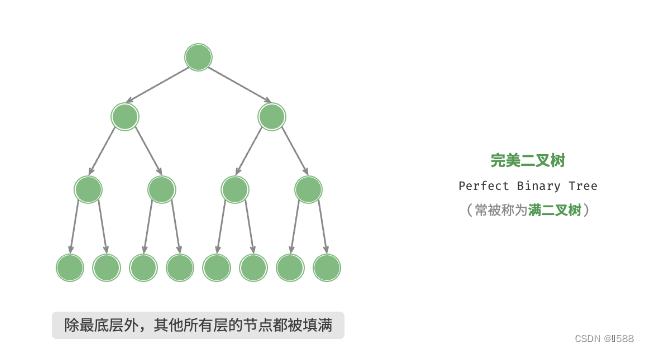
1.完美二叉树（满二叉树）： 除了最底层外，其余所有层的节点都被完全填满。最底层节点尽量靠左填充。

在完美二叉树中，叶节点的度为 0 ，其余所有节点的度都为 2 ；若树高度为h，则节点总数为2的（h+1）次幂-1 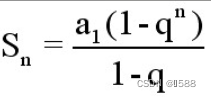   （n从1开始）

 

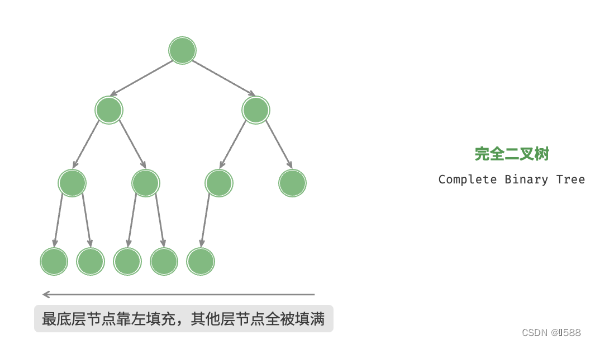
2、完全二叉树：只有最底层的节点未被填满，且最底层节点尽量靠左填充。

 

3、完满二叉树：除了叶节点之外，其余所有节点都有两个子节点。

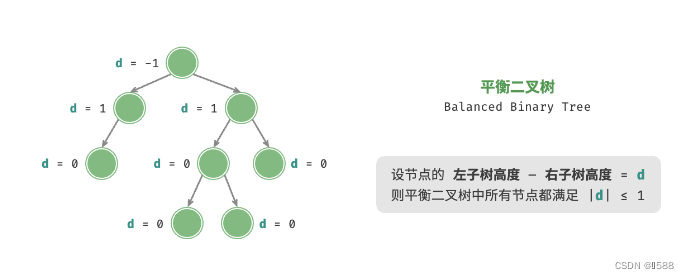
4、平衡二叉树：任意节点的左子树和右子树的高度之差的绝对值不超过 1 。

当二叉树所有节点偏向一层的时候。二叉树退化为链表。 

知识点2：二叉树遍历：分为层序遍历、前序遍历、中序遍历和后序遍历等。

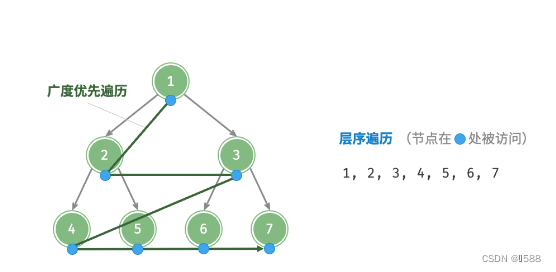
        ①层序遍历：从顶部到底部逐层遍历二叉树，并在每一层按照从左到右的顺序访问节点。属于广度优先搜索BF（优先搜索距离近的）。O（n）

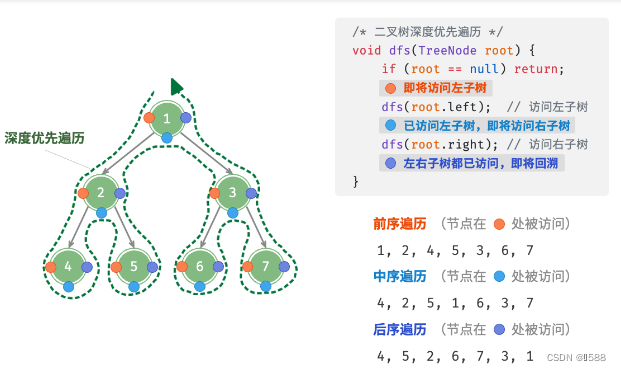
        ② 前序、中序、后序遍历：深度优先遍历DF（优先遍历到最远的，再回溯）含义是“根结点在何时被访问”

 

 

 O（n）

                

二、二叉搜索树：

1. 对于根节点，左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值；
2. 任意节点的左、右子树也是二叉搜索树，即同样满足条件1

知识点1、查找节点：

我们声明一个节点 cur ，从二叉树的根节点 root 出发，循环比较节点值 cur.val 和 num 之间的大小关系

• 若 cur.val < num ，说明目标节点在 cur 的右子树中，因此执行 cur = cur.right ；
• 若 cur.val > num ，说明目标节点在 cur 的左子树中，因此执行 cur = cur.left ；
• 若 cur.val = num ，说明找到目标节点，跳出循环并返回该节点；

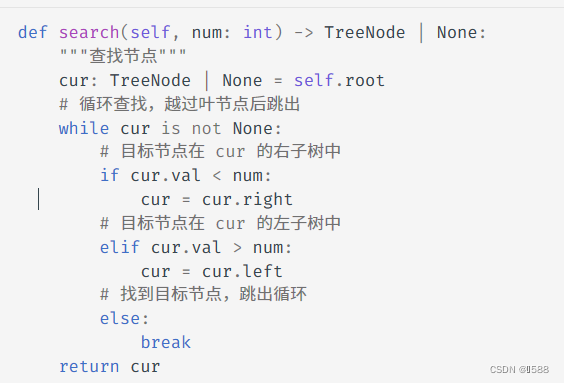
类似二分查找，O（logn） 

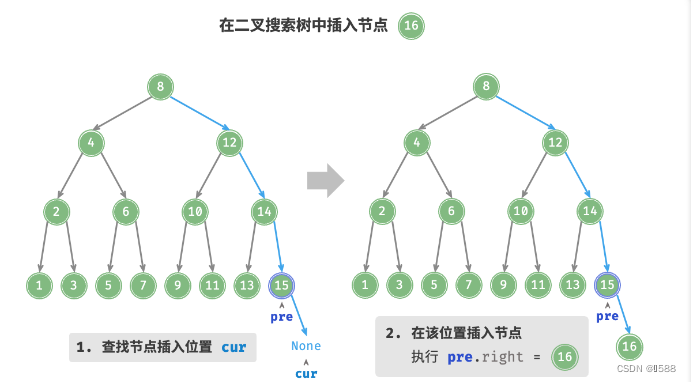
知识点2、插入节点：

1. 查找插入位置：与查找操作相似，从根节点出发，根据当前节点值和 num 的大小关系循环向下搜索，直到越过叶节点（遍历至 None ）时跳出循环；
2. 在该位置插入节点：初始化节点 num ，将该节点置于 None 的位置；

二叉搜索树不允许存在重复节点，否则将违反其定义。因此，若待插入节点在树中已存在，则不执行插入，直接返回。O（logn）

 知识点3、删除节点O（logn）：当待删除节点的子节点数量 =0 时，表示待删除节点是叶节点，可以直接删除；当待删除节点的子节点数量 =1 时，将待删除节点替换为其子节点即可；

当待删除节点的子节点数量 =2 时，删除操作分为三步：

1. 找到待删除节点在“中序遍历序列”中的下一个节点，记为 tmp ；
2. 在树中递归删除节点 tmp ；
3. 用 tmp 的值覆盖待删除节点的值；

 

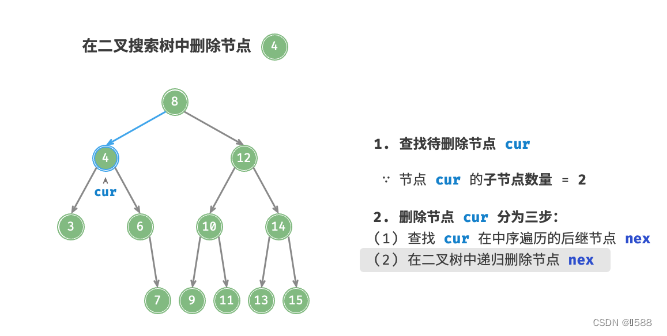
PS：这里有两种选法：

1. 选择该节点的左子树中的最大节点；
2. 选择该节点的右子树中的最小节点；

文中采取的是方法 2

知识点4、排序

二叉搜索树的中序遍历序列是升序的。所以在二叉搜索树中获取有序数据的时间复杂度是O（n）

三、AVL树：平衡二叉搜索树

二叉搜索树在多次插入和删除之后，可能退化成链表，那么时间复杂度就会变成O（n）。「AVL 树」既是二叉搜索树也是平衡二叉树，同时满足这两类二叉树的所有性质，因此也被称为「平衡二叉搜索树」。

每个node的性质有：val,height,left,right

height是指从该节点到最远叶节点的距离，即所经过的“边”的数量。叶节点的高度为 0 ，而空节点的高度为 -1 。

节点的「平衡因子 Balance Factor」定义为节点左子树的高度减去右子树的高度，同时规定空节点的平衡因子为 0 。PS：设平衡因子为 f，则一棵 AVL 树的任意节点的平衡因子皆满足 −1 ≤ f ≤ 1 。

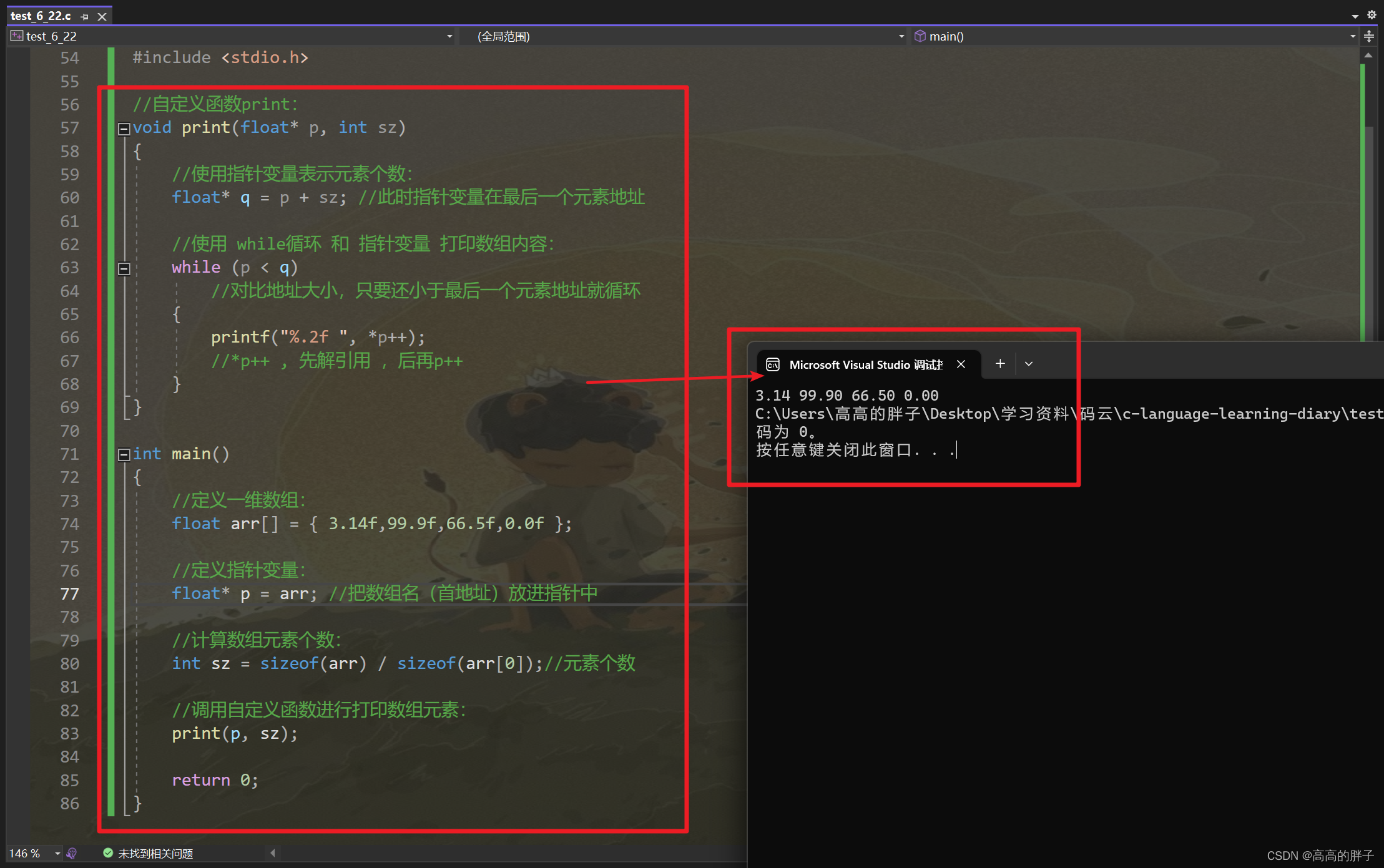
知识点1、AVL树旋转

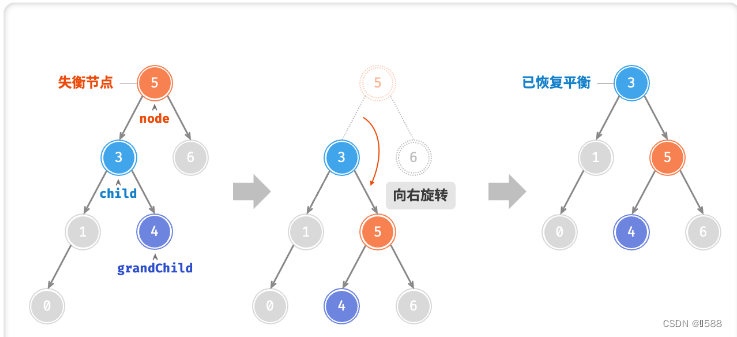
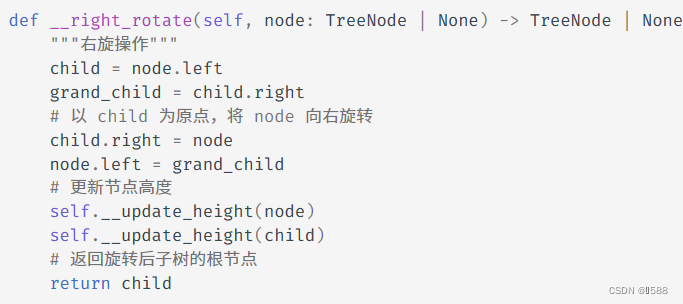
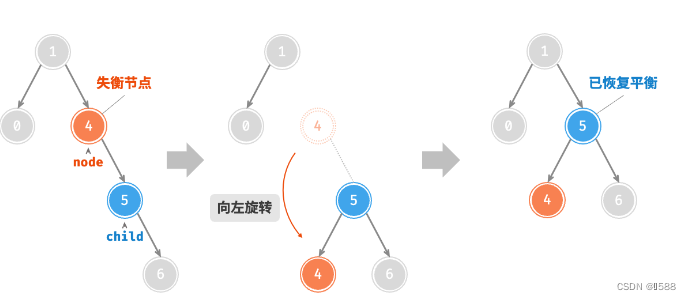
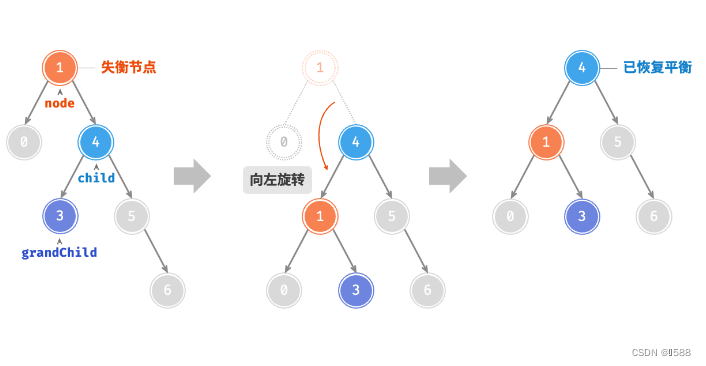
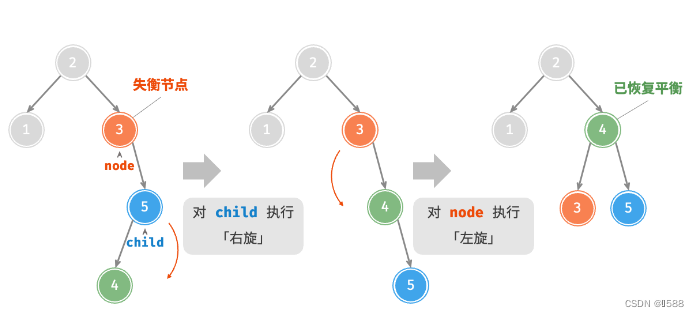
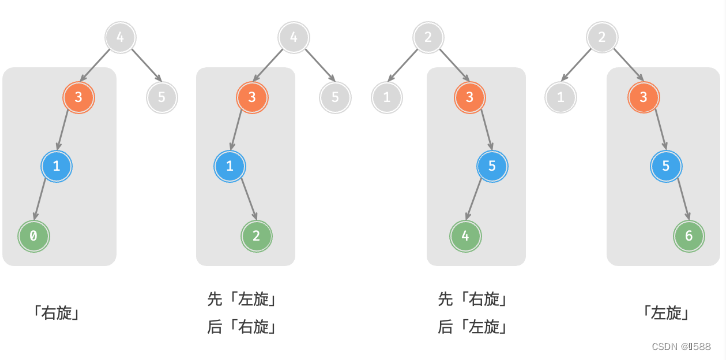
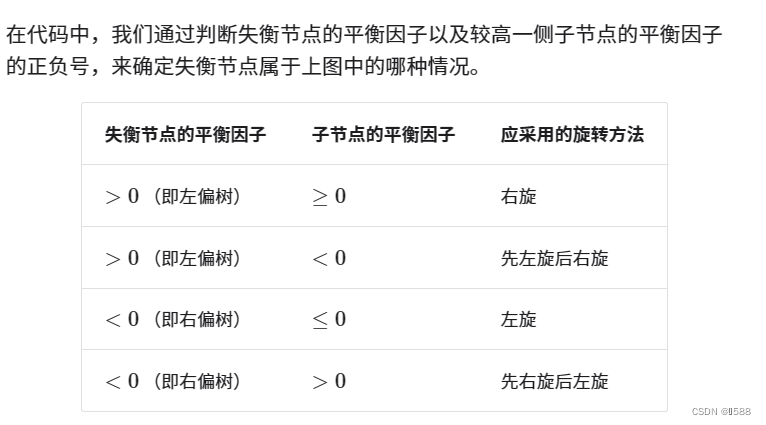
AVL 树的特点在于「旋转 Rotation」操作，它能够在不影响二叉树的中序遍历序列的前提下，使失衡节点重新恢复平衡。换句话说，旋转操作既能保持树的「二叉搜索树」属性，也能使树重新变为「平衡二叉树」。将平衡因子绝对值 >1 的节点称为「失衡节点」。根据节点失衡情况的不同，旋转操作分为四种：右旋、左旋、先右旋后左旋、先左旋后右旋。

①：右旋

情况1

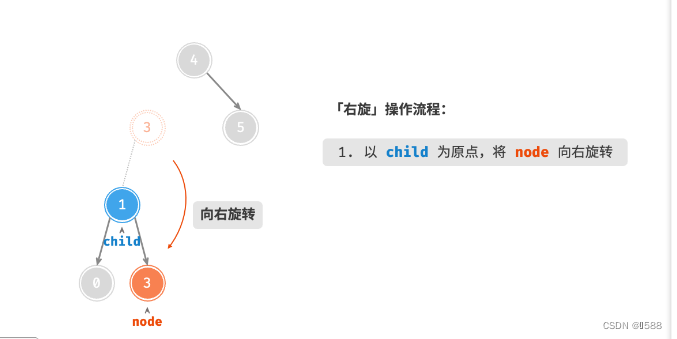
 情况2

 

②：左旋

 情况1

情况2

 

 

③：先左旋再右旋

（对child左旋，再对自己右旋）

 

 

④：先右旋再左旋

（对child右旋再对自己左旋）

旋转的选择：

 

 

 知识点二、AVL树常用操作

1、插入节点，像二叉搜索树一样插入，在每次插入之后进行rotate

2、删除节点，像二叉搜索树一样删除，每次删除之后进行rotate

3、查找节点（与二叉搜索树一样）

红黑树的平衡条件相对宽松，因此在红黑树中插入与删除节点所需的旋转操作相对较少，在节点增删操作上的平均效率高于 AVL 树。