实验 4：排序与查找

news2024/9/22 5:32:01
  • 东莞理工的学生可以借鉴，请勿抄袭

1.实验目的

通过实验达到：

  1. 理解典型排序的基本思想，掌握典型排序方法的思想和相应实现算法；

  2. 理解和掌握用二叉排序树(BST)实现动态查找的基本思想和相应的实现 算法。

  3. 理解和掌握哈希(HASH)存储结构的基本思想、哈希查找的思想、实现；

  4. 掌握典型查找、排序算法的算法分析。

2. 题目 1：排序

① 用 C 的 rand 函数随机生成若干个（例如 20-1000 个）在某个区间（例如 [0, 10000]）之间的整数保存数组中，以此数组元素作为关键字；

② 采用堆排序算法按非递增方式（从大到小）进行排序，给出操作的结果 及相应的操作次数（比较次数、移动次数）；

③ 采用快速排序算法按非递增方式（从大到小）进行排序，给出操作的结 果及相应的操作次数； ④ 采用归并排序算法按非递增方式（从大到小）进行排序，给出操作的结 果及相应的操作次数；

⑤ 主函数通过调用函数实现以上操作。

附加题：（每完成一个额外附加 5 分，上限 10 分）

① 10-27 设带头结点的单链表 L 中存放着要排序的 int 类型的若干个数据 元素，编写函数实现单链表存储结构的冒泡排序。

② 10-28 设带头结点的单链表 L 中存放着要排序的 int 类型的若干个数据 元素，编写函数实现单链表存储结构的直接选择排序。

③ 10-29 基数排序算法设计。

要求:

(1)设计基于顺序队列的基数排序函数。

(2)设计一个测试主函数，测试所设计的基于顺序队列的基数排序函数。

2.1. 数据结构设计

整形数组

2.2. 主要操作算法设计与分析

2.2.1. 获取随机数数组方法

int* createRandom()

返回类型：int*；

是否有参数：无

步骤：

  1. 通过srand和rand配合获取随机数（mod 10001）
  2. 用for循环获取N个

算法时间复杂度：

  • 时空复杂度为O(N);

2.2.2 打印数组函数

void display(int elem[])

返回类型：无；

是否有参数：无

步骤：

  1. 遍历数组打印每一个元素

算法时间复杂度：

  • 时间复杂度为O(N);

2.2.3. 堆排序函数

void heapSort(int elem[])

void createHeap(int elem[])

void shiftDown(int* elem, int root, int len)

返回类型：无返回值；

是否有参数：有，待排序数组

步骤：

  1. 调用createHeap对elem数组进行建堆操作
  2. 从(N - 2) / 2开始到0，对elem进行向下过滤的调整堆shiftDown操作
  3. 循环结束排序完成

算法时间复杂度：

  • 时间复杂度为O(Nlog2N);

2.2.4. 快速排序

void quickSort(int* arr)

void quick(int* arr, int left, int right)

int partition(int* arr, int left, int right)

int findMid(int* arr, int left, int right)

返回类型：无返回值；

是否有参数：有，待排序数组

步骤：

  1. 调用递归函数quick，传入left 0，right N-1
  2. 如果left大于等于right，直接返回
  3. 调用findMid找到数组的left到right这一部分数组中的中间值下标（三值取中），找到后这个下标与第一个元素进行交换
  4. 调用partition函数，进行快排划分，返回一个基准值pivot
  5. 调用quick，传入arr，左半部分
  6. 调用quick，传入arr，右半部分

算法时间复杂度：

  • 时间复杂度为O(Nlog2N);

2.2.5. 归并排序函数

void mergeSort(int* arr)

void mergeSorter(int* arr, int left, int right)

void merge(int* arr, int left, int right, int mid)

无返回值，有参数，待排序数组

步骤：

  1. 调用递归函数mergeSorter，传入arr，left，right
  2. 获得left和right中间值，mid
  3. 调用merge函数，传入arr，left，right，和mid
    • 合并有序顺序表操作
  4. 将左半部分和右半部分进行重复操作
  5. 最终排序完毕

复杂度分析：

时间复杂度：O(Nlog2N)

2.2.6. 主函数设计

int main() {
    int* arr = createRandom();
    heapSort(arr);
    printf("比较次数：%d, 交换次数：%d\n", compareCount, moveCount);
    display(arr);
    free(arr);
    arr = createRandom();
    quickSort(arr);
    printf("快排划分次数：%d\n", quickSortCount);
    display(arr);
    free(arr);
    arr = createRandom();
    mergeSort(arr);
    printf("归并次数：%d\n", mergeCount);
    display(arr);
    free(arr);
    return 0;
}

2.3. 程序运行过程及结果

在这里插入图片描述

3. 题目 2：二叉排序树(Binary Sort Tree, BST)的建立及动态查 找

生成若干个（比如 50 个）在某个区间（例如[-1000, 1000]）之间互不相同的 整数保存在数组 A 中，以此数组元素作为关键字，设计实现以下操作的程序：

① 建立对应的二叉排序树，按中序遍历算法输出所建立的 BST 树的结点；

② 对该二叉排序树，查找指定的关键字（输入要查找的整数），给出操作 的结论及相应的操作次数（比较次数）；

③ 对该二叉排序树，删除指定的关键字（输入要删除的整数），给出操作 的结论及相应的操作次数；

④ 按中序遍历算法输出二叉排序树的所有结点；

⑤ 主函数通过调用函数实现以上操作。

3.1. 数据结构设计

struct TreeNode {
    int val;
    struct TreeNode* left;
    struct TreeNode* right;
};

3.2. 主要操作算法设计与分析

3.2.1 创建以及中序遍历

  1. void freeTree(struct TreeNode* root)：

该函数用于释放二叉树的内存空间，它的具体步骤是：

  • 如果传入的 root 指针为空，则直接返回。
  • 否则，递归地释放其左子树的空间。
  • 接着，递归地释放其右子树的空间。
  • 最后，释放当前节点的空间。
  1. void inorderTraversal(struct TreeNode* root)：

该函数用于对二叉树进行中序遍历，并将节点的值依次输出到控制台中，具体步骤是：

  • 如果传入的 root 指针为空，则直接返回。
  • 否则，以递归的方式，先遍历左子树。
  • 然后输出当前节点的值。
  • 最后以递归的方式，遍历右子树。

算法时间复杂度：

  • 时空复杂度为O(N);

3.2.2 查找函数

该代码实现了在二叉搜索树中查找目标节点的功能，具体步骤如下：

  1. 如果传入的根节点指针 root 为空或者根节点的值就是目标值 target，那么增加一次比较次数 cmp 的计数器，并返回根节点指针 root。

  2. 如果目标值 target 小于根节点的值，那么增加两次比较次数 cmp 的计数器，然后递归地对根节点的左子树进行搜索。

  3. 否则，增加两次比较次数 cmp 的计数器，然后递归地对根节点的右子树进行搜索。

在这个过程中，计数器 cmp 用于记录比较目标值的次数，最终返回的是查找到的目标节点的指针，如果没有找到目标节点，返回空指针。

算法时间复杂度：

  • 时空复杂度为O(log2N);

3.2.3. 插入函数

struct TreeNode* insert(struct TreeNode* root, int val, int* cmp)

该代码实现了往二叉搜索树中插入一个节点的功能，具体说明如下：

传入参数：

  • root: 指向二叉搜索树根节点的指针。
  • val: 待插入的节点的值。
  • cmp: 指向用于记录比较次数的计数器的指针。

返回值：

  • 返回指向插入节点后的二叉搜索树根节点的指针。

具体步骤：

  1. 如果传入的根节点指针 root 为空，则增加一次比较次数 cmp 的计数器，并为新节点分配内存空间，然后创建该新节点，并将其左右指针都置为空，最后返回该新节点的指针。

  2. 如果目标值 val 小于根节点的值，则增加两次比较次数 cmp 的计数器，然后递归地将节点插入到根节点的左子树中，然后将该节点的左子节点指针指向递归返回的节点的指针。

  3. 否则，增加两次比较次数 cmp 的计数器，然后递归地将节点插入到根节点的右子树中，然后将该节点的右子节点指针指向递归返回的节点的指针。

算法时间复杂度：

  • 时空复杂度为O(log2N);

3.2.4 删除函数

struct TreeNode* delete(struct TreeNode* root, int target, int* cmp)

该代码实现了从二叉搜索树中删除一个节点的功能，具体说明如下：

传入参数：

  • root: 指向二叉搜索树根节点的指针。
  • target: 待删除节点的值。
  • cmp: 指向用于记录比较次数的计数器的指针。

返回值：

  • 返回指向删除节点后的二叉搜索树根节点的指针。

具体步骤：

  1. 如果传入的根节点指针 root 为空，则增加一次比较次数 cmp 的计数器，并返回空指针。

  2. 如果目标值 target 小于根节点的值，则增加两次比较次数 cmp 的计数器，然后递归地从根节点的左子树中删除目标节点，并将根节点的左子节点指针指向递归返回的节点的指针。

  3. 否则，如果目标值 target 大于根节点的值，则增加两次比较次数 cmp 的计数器，然后递归地从根节点的右子树中删除目标节点，并将根节点的右子节点指针指向递归返回的节点的指针。

  4. 如果目标值 target 等于根节点的值，则判断根节点是否存在左右子树：

  • 如果不存在左子树，则直接将根节点的右子树作为新的根节点，然后释放原根节点的内存空间。
  • 如果不存在右子树，则直接将根节点的左子树作为新的根节点，然后释放原根节点的内存空间。
  • 如果既有左子树又有右子树，则找到右子树中最小（或左子树中最大）的节点 cur，把其值赋给根节点，然后递归地从右子树中删除该最小节点的值，将根节点的右子节点指针指向递归返回的节点的指针。

算法时间复杂度：

  • 时间空间复杂度为O(log2N);（准确的来说是树的高度）

3.2.5. 主函数设计

int main() {
    int n = 50; // 数组元素个数
    int* arr = (int*)malloc(n * sizeof(int));
    srand(time(NULL));
    for (int i = 0; i < n; i++) {
        arr[i] = rand() % 2001 - 1000; // 随机生成-1000至1000之间的整数
        for (int j = 0; j < i; j++) { // 把相同的数过滤掉
            if (arr[i] == arr[j]) {
                i--;
                break;
            }
        }
    }

    struct TreeNode* root = NULL;
    int cmp = 0;

    for (int i = 0; i < n; i++) {
        root = insert(root, arr[i], &cmp);
    }
    printf("Inorder traversal of the BST:\n");
    inorderTraversal(root);
    printf("\n\n");

    int target;
    printf("请输入你想查找的节点： ");
    scanf("%d", &target);
    struct TreeNode* found = search(root, target, &cmp);
    if (found == NULL) {
        printf("找不到\n");
    }
    else {
        printf("Element %d 被找到了\n", found->val);
    }
    printf("比较操作次数：%d \n", cmp);

    int delete_val;
    printf("请输入你要删除的节点: ");
    scanf("%d", &delete_val);
    root = delete(root, delete_val, &cmp);
    if (root == NULL) {
        printf("树空了！");
    }
    else {
        printf(" %d 被删了，中序序列为:\n", delete_val);
        inorderTraversal(root);
    }
    printf("\n%d为比较次数.\n", cmp);

    printf("\n中序序列为:\n");
    inorderTraversal(root);
    printf("\n");

    freeTree(root);
    free(arr);

    return 0;
}

3.3. 程序运行过程及结果

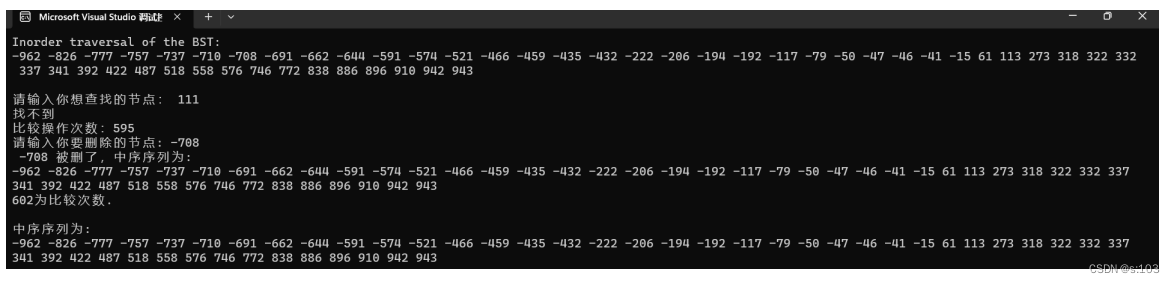
在这里插入图片描述

4. 题目 3：哈希表(HASH)的建立及查找（选做题）

4.1. 数据结构设计

const int MAX_CAPACITY = 20; // 哈希表大小
const int PRIME_NUM = 17; // 哈希函数的p值

// 哈希表节点
struct Node {
    int val;
    struct Node* next;
};

4.2. 主要操作算法设计与分析

4.2.1 创建函数

hashFunc 函数：

传入参数：

  • key: 待哈希的关键字。

返回值：

  • 哈希函数计算出的哈希值。

步骤：

  • 对传入的关键字 key 取模 PRIME_NUM，然后再加上 PRIME_NUM，最后再对 PRIME_NUM 取模，得到哈希函数的计算结果。

createNode 函数：

传入参数：

  • val: 新节点的值。

返回值：

  • 指向新节点的指针。

步骤：

  • 分配一个大小为 struct Node 的内存空间 node。
  • 将节点的 val 值设为传入的值 val。
  • 将节点的 next 指针设为空指针。
  • 返回指向新节点的指针。

这两个函数的时间复杂度和空间复杂度都比较低，hashFunc 函数的时间复杂度为 O(1)，createNode 函数的时间复杂度也为 O(1)，它们的空间复杂度也都为 O(1)。

4.2.2 查找函数

// 查找哈希表中值为target的节点，返回该节点所在的哈希表位置（下标） int search(struct Node** hashTable, int target, int* cmp)

传入参数：

  • hashTable: 指向哈希表首地址的指针。
  • target: 待查找的值。
  • cmp: 指向用于记录比较次数的计数器的指针。

返回值：

  • 如果在哈希表中找到了值为 target 的节点，则返回该节点所在的哈希表位置（下标）。
  • 如果在哈希表中没有找到值为 target 的节点，则返回 -1。

步骤：

  • 首先根据哈希函数计算出待查找值 target 的哈希表位置 index。
  • 然后在哈希表的 index 位置处查找与 target 相等的节点。
  • 如果找到了与 target 相等的节点，则直接返回该节点所在的哈希表位置 index。
  • 如果没找到与 target 相等的节点，则将指针 cur 指向哈希表中下一个节点，继续比较，直到遍历完所有的节点。
  • 如果最终仍未找到与 target 相等的节点，则返回 -1。

算法复杂度分析：

该函数的时间复杂度与平均每个位置的链表长度有关，为 O(1+K)，其中 K 表示平均每个位置的链表长度。该函数的空间复杂度为 O(n)，其中 n 表示哈希表中节点的数量。

4.2.3. 插入函数

void insert(struct Node** hashTable, int val, int* cmp)

该代码实现了往哈希表中插入一个新节点的功能，具体说明如下：

传入参数：

  • hashTable: 指向哈希表首地址的指针。
  • val: 待插入节点的值。
  • cmp: 指向用于记录比较次数的计数器的指针。

返回值：

  • 无返回值。

具体步骤：

  • 首先根据哈希函数计算出待插入节点的哈希表位置 index。
  • 如果该位置下的链表为空，则直接在该位置处创建一个新节点，并将该节点插入到链表的首位。
  • 如果该位置下的链表不为空，则需要查找链表的末尾，然后在末尾处创建一个新节点，并将其插入到链表的末尾。

算法时间复杂度：

该函数的时间复杂度取决于链表长度，并且最坏情况的时间复杂度为 O(n)，其中 n 表示链表的长度。该函数的空间复杂度取决于哈希表的大小和节点个数，因为哈希表中的每个位置都可能含有多个节点，所以空间复杂度最坏情况下为 O(n)，其中 n 表示节点的数量。

4.2.4 删除函数

void delete(struct Node** hashTable, int target, int* cmp)

传入参数：

  • hashTable: 指向哈希表首地址的指针。
  • target: 待删除节点的值。
  • cmp: 指向用于记录比较次数的计数器的指针。

返回值：

  • 无返回值。

步骤：

  • 首先根据哈希函数计算出值为 target 的节点所在的哈希表位置 index。
  • 然后在哈希表的 index 位置处查找与 target 相等的节点 cur，如果 cur 节点不存在（即该位置下的链表为空），则直接返回。
  • 如果 cur 节点恰好就是哈希表里的第一个节点，则将哈希表的 index 位置指向 cur 的下一个节点，然后释放 cur 指向节点的内存空间。
  • 如果 cur 节点不是哈希表的第一个节点，则需要沿着链表继续查找，直到找到与 target 相等的节点 temp。
  • 当找到与 target 相等的节点 temp 时，先将该节点的前一个节点 cur 的 next 指针指向 temp 节点的下一个节点，然后释放 temp 指向节点的内存空间即可。

算法时间复杂度：

  • 该函数的时间复杂度取决于链表长度，并且最坏情况的时间复杂度为 O(n)，其中 n 表示链表的长度。该函数的空间复杂度为 O(1)。

4.2.5. 输出哈希表

void printHashTable(struct Node** hashTable)

传入参数：

  • hashTable: 指向哈希表首地址的指针。

返回值：

  • 无返回值。

具体步骤：

  • 遍历整个哈希表，对于每个位置 i，输出该位置对应的链表中所有节点的值。

注意：需要在每个节点的值之间输出空格，最后需要在每行输出结束后换行。

算法复杂度分析：

  • 该函数的时间复杂度为 O(n)，其中 n 表示哈希表中节点的数量。该函数的空间复杂度为 O(1)。

4.2.6. 主函数设计

int main() {
        int n = 50; // 数组元素个数
    int* arr = (int*)malloc(sizeof(int) * n);
    srand(0);
    for (int i = 0; i < n; i++) {
        arr[i] = rand() % 901 + 100; // 随机生成100至1000之间的整数
        for (int j = 0; j < i; j++) { // 把相同的数过滤掉
            if (arr[i] == arr[j]) {
                i--;
                break;
            }
        }
    }

    struct Node* hashTable = (struct Node*)calloc(MAX_CAPACITY, sizeof(struct Node));
    int cmp = 0;

    // 建立哈希表
    for (int i = 0; i < n; i++) {
        insert(hashTable, arr[i], &cmp);
    }
    printf("哈希表已建立：\n");
    printHashTable(hashTable); // 输出哈希表
    printf("\n");

    // 查找
    int target;
    printf("请输入要查找的元素：");
    scanf("%d", &target);
    int index = search(hashTable, target, &cmp);
    if (index < 0) {
        printf("没有找到该元素。\n");
    }
    else {
        printf("找到了元素 %d，它在哈希表的位置是 %d。\n", target, index);
    }
    printf("总共进行了 %d 次比较。\n", cmp);
    printf("\n");

    // 删除
    int delete_val;
    printf("请输入要删除的元素：");
    scanf("%d", &delete_val);
    delete(hashTable, delete_val, &cmp);
    printf("元素 %d 已删除。\n", delete_val);
    printf("删除后的哈希表：\n");
    printHashTable(hashTable); // 输出哈希表
    printf("总共进行了 %d 次比较。\n", cmp);

    free(arr);
    free(hashTable);

    return 0;
}

4.3. 程序运行过程及结果

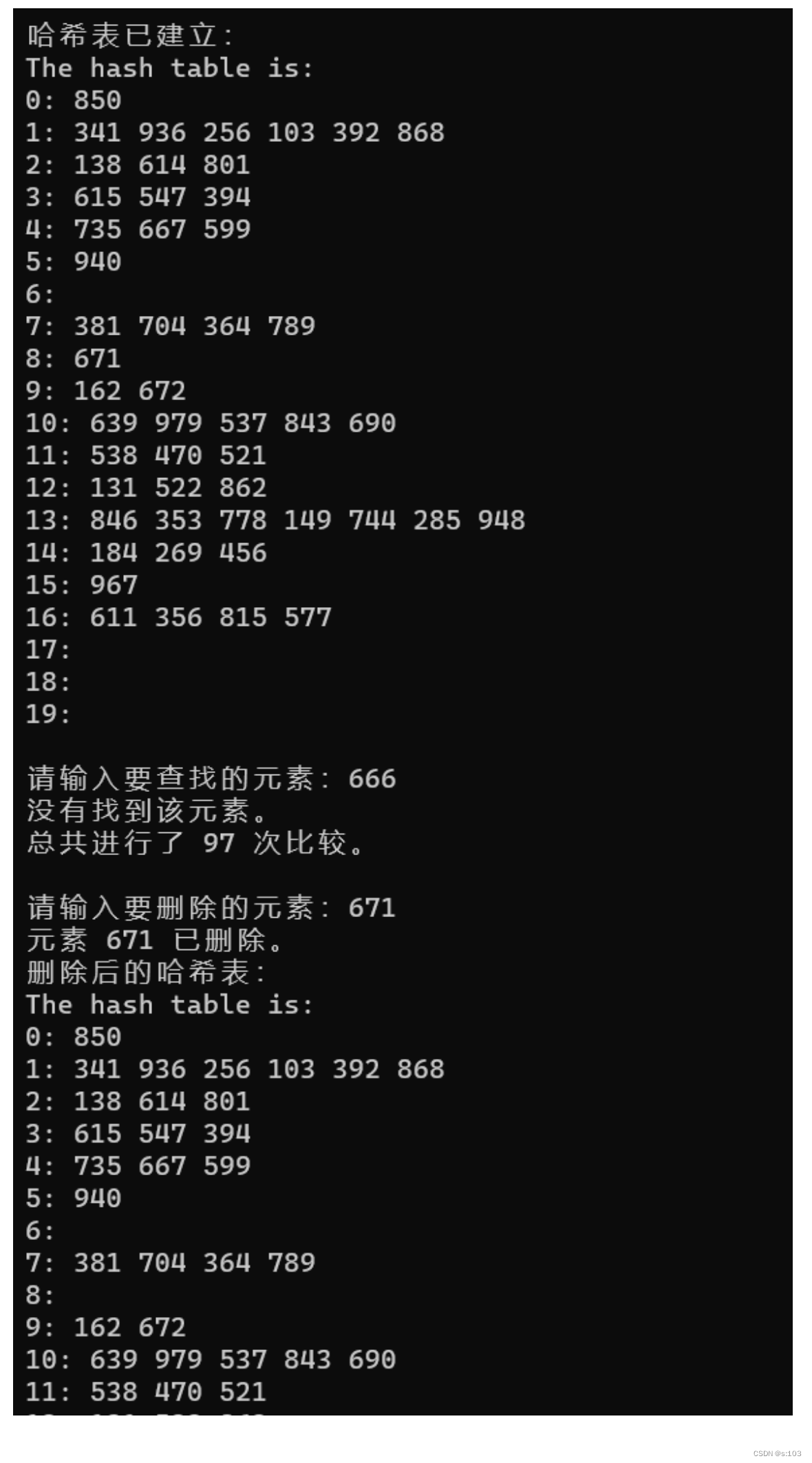
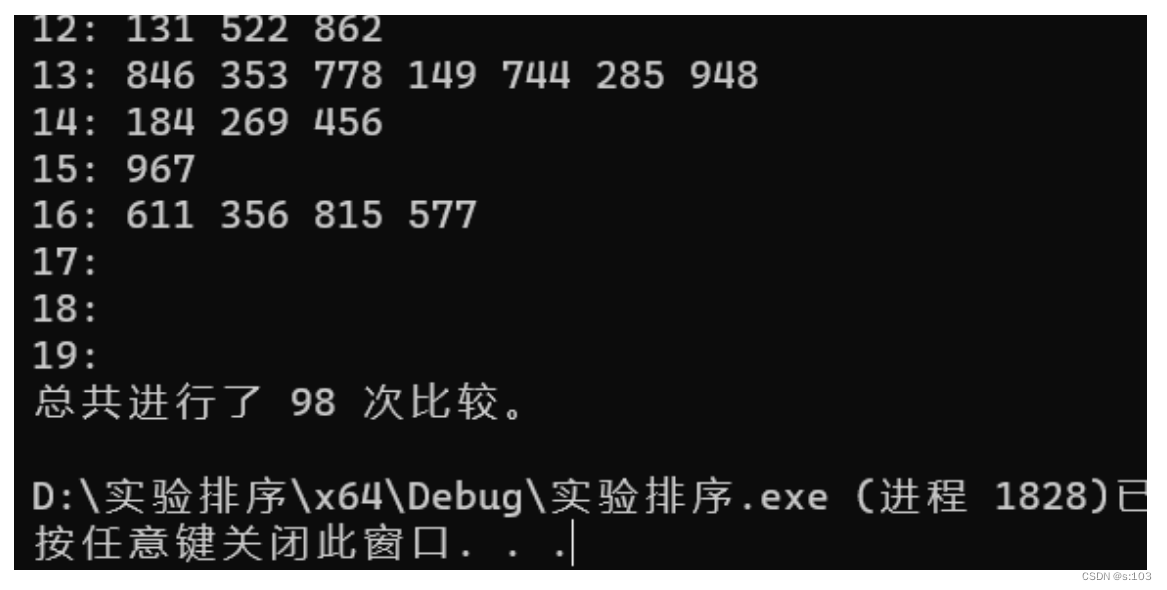
在这里插入图片描述
在这里插入图片描述

5. 总结

  1. 快速排序使用分治策略实现，时间复杂度平均为 O(nlogn)，但最坏情况下会退化为 O(n^2)。
  2. 归并排序同样也使用分治策略实现，时间复杂度稳定为 O(nlogn)，但需要使用额外的空间存储中间结果。
  3. 堆排序的时间复杂度也为 O(nlogn)，且不需要使用额外空间，但排序结果不稳定。
  4. 哈希表通过哈希函数将数据映射为连续空间上的一个位置，能够实现常数时间内的查找操作，但哈希函数的选择与负载因子会影响哈希表的性能。
  5. 搜索树通过以节点间的关系来描述数据之间的有序关系（如二叉搜索树），能够实现 O(logn) 的时间复杂度，但最坏情况下也可能变为 O(n)。不同的算法适用于不同的场景，需要根据具体应用场景结合时间和空间复杂度进行合理选择。

6. 附录：源代码

我已上传附件：“实验排序.zip”

码云链接：排序与查找

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/675123.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【备战秋招】每日一题:2023.04.26-实习-第三题-MC方块

【备战秋招】每日一题:2023.04.26-实习-第三题-MC方块

在线评测链接:P1231 题目内容 MC最新版本更新了一种特殊的方块&#xff0c;幽匿催发体。这种方块能够吸收生物死亡掉落的经验并感染周围方块&#xff0c;使其变成幽匿块。Steve想要以此为基础尝试搭建一个经验仓库&#xff0c;他来到了创造超平坦模式&#xff0c;在只有草方块…
阅读更多...
[进阶]junit单元测试框架详解

[进阶]junit单元测试框架详解

单元测试 就是针对最小的功能单元(方法&#xff09;&#xff0c;编写测试代码对其进行正确性测试。 以前是如何进行单元测试的&#xff1f;有什么问题&#xff1f; 只能在main方法编写测试代码&#xff0c;去调用其他方法进行测试。无法实现自动化测试&#xff0c;一个方法测…
阅读更多...
python数字猜谜2.0

python数字猜谜2.0

改进了一下数字猜谜&#xff1a; 开头&#xff0c;可选等级&#xff1a; import random guess -1 c 0 print("数字猜谜游戏&#xff01;") n input("选择等级 A B C&#xff1a;") if (n "A") or (n "a"):guess random.randint…
阅读更多...
模拟电路系列分享-阻容的频率响应

模拟电路系列分享-阻容的频率响应

目录 概要 整体架构流程 技术名词解释 技术细节 1.以低通为例 2.高通电路&#xff1a; 总结&#xff1a; 概要 提示&#xff1a;这里可以添加技术概要 接着上一节的内容&#xff0c;这一节我们将介绍阻容的频率响应 整体架构流程 提示&#xff1a;这里可以添加技术整体架构…
阅读更多...
模拟电路系列文章-放大电路输出电容

模拟电路系列文章-放大电路输出电容

目录 概要 整体架构流程 技术名词解释 技术细节 小结 概要 提示&#xff1a;这里可以添加技术概要 一个运放组成的同相比例器&#xff08;包含运放内部结构&#xff09;所示&#xff0c;在它的输出端对地接了一个大电容C&#xff0c;这是一个极其危险的电路&#xff0c;一般会…
阅读更多...
Java注解以及BigInteger类、BigDecimal类

Java注解以及BigInteger类、BigDecimal类

说明&#xff1a; ① java.math包的BigInteger可以表示不可变的任意精度的整数。 ② 要求数字精度比较高&#xff0c;用到java.math.BigDecimal类 15是精度 后面大写的字母是要求要四舍五入 注解的理解 ① jdk 5.0 新增的功能 ② Annotation 其实就是代码里的特殊标记, 这些标…
阅读更多...
C语言：使用指针打印数组内容

C语言：使用指针打印数组内容

题目&#xff1a; 写一个函数打印arr数组的内容&#xff0c;不使用数组下标&#xff0c;使用指针。 arr是一维数组。 思路一&#xff1a;用 for循环 进行循环打印&#xff08;未写自定义函数&#xff09; 总体思路&#xff1a; &#xff08;一&#xff09;. 定义一维数组arr&a…
阅读更多...
基于Hexo和Butterfly创建个人技术博客，(14) 给博客站点添加Aplayer音乐

基于Hexo和Butterfly创建个人技术博客，(14) 给博客站点添加Aplayer音乐

Hexo官司网查看 这里 本章目标&#xff1a; 掌握aplayer音乐插件的用法给博客站点添加音乐功能 一、概述 个人比较倾向网站以简洁为主&#xff0c;并不赞成把网站做成花里虎哨的&#xff0c;比如添加鼠标特效或各种动态的元素。但个人站点的随意性比较大&#xff0c;虽没必要做…
阅读更多...
【C++】内存管理、new和delete操作类型、operator new和operator delete函数、new和delete的实现原理

【C++】内存管理、new和delete操作类型、operator new和operator delete函数、new和delete的实现原理

文章目录 1.C/C内存管理2.C语言的内存管理方式3.C内存管理方式3.1 new和delete操作内置类型3.2 new和delete操作自定义类型 4.operator new与operator delete函数5.new和delete的实现原理5.1内置类型5.2 自定义类型 1.C/C内存管理 在C/C中&#xff0c;内存管理是程序员负责管理…
阅读更多...
2023.6.20-【personal training】：键盘输入整数，求其和与平均数。并对每一次键入都实现自主控制。

2023.6.20-【personal training】：键盘输入整数，求其和与平均数。并对每一次键入都实现自主控制。

代码&#xff1a; #define _CRT_SECURE_NO_WARNINGS 1 #include<stdio.h> int main() { int a 0; int sum 0; double ave 0; double sum2 0; int qua 0; int tri ; printf("请输入一个整数&#xff1a;"); tri scanf_s("%d", &a); while …
阅读更多...
华为OD机试真题 JavaScript 实现【最短木板长度】【2022Q4 100分】，附详细解题思路

华为OD机试真题 JavaScript 实现【最短木板长度】【2022Q4 100分】，附详细解题思路

一、题目描述 小明有 n 块木板&#xff0c;第 i ( 1 ≤ i ≤ n ) 块木板长度为 ai。 小明买了一块长度为 m 的木料&#xff0c;这块木料可以切割成任意块&#xff0c;拼接到已有的木板上&#xff0c;用来加长木板。 小明想让最短的木板尽量长。 请问小明加长木板后&#xff0c…
阅读更多...
2023.6.15钛动科技java实习第一轮技术面试

2023.6.15钛动科技java实习第一轮技术面试

第一次面试&#xff0c;又是在考六级期间&#xff0c;也缺乏经验和准备。无笔试&#xff0c;问的简历项目比较多&#xff0c;java基础较多&#xff0c;聊了半个小时。这次的面试应该是挂掉的&#xff0c;面试官建议我多背背八股文和面试题哈 线下面试问题&#xff08;无笔试&a…
阅读更多...
Redis持久化机制与Redis事务

Redis持久化机制与Redis事务

一、Redis 持久化机制 Redis 是个基于内存的数据库。那服务一旦宕机&#xff0c;内存中数据必将全部丢失。所以丢失数据的恢复对于 Redis 是十分重要的&#xff0c;我们首先想到是可以从数据库中恢复&#xff0c;但是在由 Redis 宕机时&#xff08;说明相关工作正在运行&#…
阅读更多...
Python打包，嵌入式方式打包，而且是官方推荐的打包方式-Python嵌入式打包真的不如pyinstaller吗?

Python打包，嵌入式方式打包，而且是官方推荐的打包方式-Python嵌入式打包真的不如pyinstaller吗?

嵌入式打包&#xff1a; 解释&#xff1a; 用嵌入式版本的python解释器进行打包程序&#xff0c;python有嵌入式版本&#xff0c;而且这个嵌入式版本的解释器大小很小&#xff0c;可以很好的省磁盘空间&#xff01;&#xff01;&#xff01; 打包步骤&#xff1a; 1、从pyt…
阅读更多...
【案例实战】SpringBoot整合Redis的GEO实现查找附近门店功能

【案例实战】SpringBoot整合Redis的GEO实现查找附近门店功能

像我们平常美团点外卖的时候&#xff0c;都会看到一个商家距离我们多少米。还有类似QQ附近的人&#xff0c;我们能看到附近的人距离我们有多少米。 那么这些业务是怎么做的呢&#xff1f;是如何实现 基于位置的附近服务系统呢。 在去了解基于位置的附近服务之前&#xff0c;我…
阅读更多...
RSA算法

RSA算法

什么是RSA算法&#xff1f; 1976年以前&#xff0c;所有的加密方法都是同一种模式&#xff1a; 甲方选择某一种加密规则&#xff0c;对信息进行加密&#xff1b; 乙方使用同一种规则&#xff0c;对信息进行解密。 由于加密和解密使用同样规则&#xff08;简称"密钥"&…
阅读更多...
C语言/C++ 之 打飞机游戏

C语言/C++ 之 打飞机游戏

【项目简介】 1、设计思想&#xff1a;本项目主要是为了实现打飞机游戏&#xff0c;主要包括5个函数模块&#xff0c;和1个主函数框架。分别是chu_shi_hua();、you_cao_zuo&#xff1b;、wu_cao_zuo();、show()&#xff1b;、main();等。项目完成过程中主要运用了C/C中的输入输…
阅读更多...
蛋黄肉粽子

蛋黄肉粽子

蛋黄肉粽子 一、蛋黄肉粽子 作为中国的传统美食之一&#xff0c;蛋黄肉粽子是端午节期间必不可少的特色食品。 我在今年的端午节期间品尝了这种美食&#xff0c;不仅让我感受到了它的美味&#xff0c;也让我领略到了它背后的历史和文化底蕴。 一、蛋黄肉粽子 首先&#xff0c;就…
阅读更多...
第三方库介绍——nanomsg(高性能通信库)

第三方库介绍——nanomsg(高性能通信库)

一、nanomsg介绍 NanoMsg是一个Socket的通讯库&#xff0c;使用C语言编写实现的&#xff0c;这样就可以适用于多种操作系统&#xff0c;而且几乎不需要什么依赖&#xff0c;可扩展并且能易于使用。Nanomsg提供了几种常见的通信模式 &#xff08; 也称为“可扩展性协议” &#…
阅读更多...
C++ 第一弹入门基础

C++ 第一弹入门基础

目录 目录 1.关键字 2.命名空间 3.标准IO输入输出 4.缺省参数 5.函数重载 6.引用 7.内联函数 1.关键字 c98的关键字一共有63个 在之后用的时候都会再次详细介绍 2.命名空间 2.1什么是命名空间&#xff0c;为什么要有他&#xff1f; 在c中为了避免相同名字的变量&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023